The SIR model estimates incorrectly the basic reproduction number for the covid-19 epidemic

Introduction

At the beginning of the epidemic, and also during the first months, we have two sets of covid-19 data: Severe covid-19 cases (those in hospitals, where they were tested and confirmed), and deaths due to covid-19. Mathematical models were formulated and used to fit the epidemic curve to estimate the basic reproduction number R₀.

In the literature, the usually assumed basic reproduction number R₀ is around 2.5, see for instance [1] and [2]. The reliable estimation of R₀ is important because this number determines the magnitude of effort to eradicate infection. For instance, the efforts of vaccination to eradicate an infection must be vaccinating a fraction equal or greater than 1 − 1/R₀ of susceptibles [3]. In [4], analyzing vaccination as a control mechanism, if R₀ is reduced by the vaccine to value lower than one, the number of cases decreased following exponential-type decay.

The estimation of the basic reproduction number R₀, however, depends on the mathematical model. We consider two examples. The first model is the simplest susceptible - infectious - recovered (SIR) model, and the second is a model taking into account more aspects of the natural history of covid-19 infection encompassing the lethality rate depending on the age, called the elaborated model. These models are fitted taking into account the severe covid-19 data collections from São Paulo State (Brazil) [5] and Spain [6].

São Paulo State, Brazil, has 44.6 million inhabitants (demographic density, 177/km²) with 15.3% of the population comprised of elder individuals. The first case was registered on February 26, and partial quarantine was implemented on March 24. Considering that there is a delay around 9 days since the infection and the onset of covid-19, we estimate the basic reproduction number considering collected data from February 26 to April 2.

Spain has 47.4 million inhabitants (demographic density, 92.3/km²) with 25.8% of the population comprised of elder individuals. The first case was registered on January 31, and lockdown was implemented on March 16. Considering a delay of around 9 days, we estimate the basic reproduction number considering collected data from January 31 to March 25.

Yang et al. [7], using the elaborated model, estimated R₀ using the first period of covid-19 data representing the natural (without any interventions) epidemic, obtaining 9.24 (Sao Paulo State) and 8.0 (Spain). The estimation of R₀ based on the first period is in concordance with the definition of the basic reproduction number: Completely susceptible population without constraints (interventions) [3].

1 The SIR model

In the SIR model, the dynamical system is (the varying total population N is N = S + I + R) where the total population N obeys and ϕ and μ are, respectively, the birth and natural mortality rates, β, γ, and α are, respectively, the transmission rate, the infectious rate, and the additional mortality (lethality) rate. If ϕ = μ + αI/N, then N is constant.

In Appendix A, the steady-state corresponding to the system of equations (1) was analyzed to obtain the basic reproduction number R₀. For simplicity, let us consider ϕ = μ. The system of equations (1), using R = N − I − S, can be rewritten as 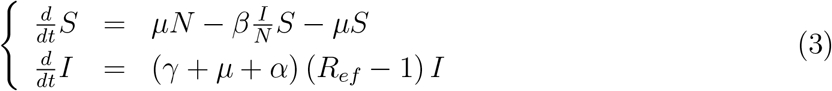where the effective reproduction number R_ef is defined by with the basic reproduction number R₀ being given by equation (A.2) changing ϕ by μ, that is, R₀ = β/ (γ + μ + α).

Let us analyze the system of equations (3) at two boundaries. Let us assume that the first case of covid-19 is introduced at t = 0, that is, the initial conditions supplied to equation (3) are S(0) = N − 1 and I(0) = 1. For a large population, we can approximate S ∼ N and the system of equations can be approximated by with R = N − S − I. Hence, at the beginning of the epidemic, if we estimate the transmission rate β, we can calculate R₀ using the expression obtained from the steady-state analysis. The system of equations (3) does not approach to a steady-state, but attains it when α = 0. In this case, asymptotically (t → ∞), we have dI/dt = 0 if R_ef = R₀S/N = 1, that is, S → S* = s*N and I → I* = i*N, where i* and s* are given by equations (A.6) and (A.7), respectively. Therefore, when α = 0, at t = 0, R_ef = R₀, and when t → ∞ (steady-state), R_ef = 1 (see equation (A.7)), from which we retrieve the well known relationship s* = 1/R₀ [3].

Therefore, based on R_ef given by equation (4) when ϕ = μ and α = 0, the basic reproduction number R₀ obtained from mathematical modelings provides two useful information: At the beginning of the epidemic (t = 0), R₀ gives the magnitude of the initial takeoff of the epidemic, and when epidemic reaches the steady-state (after many waves of the epidemic, that is, t → ∞), R₀ measures its severity providing the fraction of susceptible individuals, that is, s* = 1/R₀. Between these two extremes, the effective reproduction number R_ef dictates the course of an epidemic, which follows decaying oscillations around R_ef = 1 [4]. It is worth stressing the fact that R_ef given by equation (4) is valid only when ϕ = μ and α = 0, and when one of these conditions is not valid, R_ef given by equation (4) can be used as an approximated value.

The number of accumulated severe covid-19 cases Ω is given by the exits from S, and entering into classes I, that is, To evaluate the parameter β, we calculate where Ω^ob is the accumulated severe covid-19 registered cases. The value of β that minimizes Sum is the fitted value. We stress the fact that we are estimating the model parameters against the severe covid-19 cases.

We estimate the basic reproduction number using equation (1) with different infective persons at t = 0. The model parameters are γ = 1/10, and, for São Paulo State, ϕ = μ = 1/(78.4 × 365) and α = 0.002, and for Spain, ϕ = μ = 1/(83.4 × 365) and α = 0.002 (all in days⁻¹). The transmission rate β is estimated and the basic reproduction number R₀ is calculated using equation (A.2).

For the data collected from São Paulo State, we obtained for I(0) = 1, R₀ = 3.14 with Sum = 8.02 × 10⁵, for I(0) = 10, R₀ = 2.4 with Sum = 8.49 × 10⁵, for I(0) = 25, R₀ = 2.11 with Sum = 1.86 × 10⁶, and for I(0) = 100, R₀ = 1.62 with Sum = 5.87 × 10⁶. Other initial conditions are S(0) = 44.6 million and R(0) = 0. The lowest Sum occurs when R₀ = 3.14.

For the data collected from Spain, we obtained for I(0) = 1, R₀ = 2.97 with Sum = 4.16 × 10⁸, for I(0) = 10, R₀ = 2.5 with Sum = 6.32 × 10⁸, for I(0) = 25, R₀ = 2.3 with Sum = 1.13 × 10⁹, and for I(0) = 100, R₀ = 2.06 with Sum = 1.19 × 10⁹. Other initial conditions are S(0) = 47.4 million and R(0) = 0. The lowest Sum occurs when R₀ = 2.97.

We observed that the larger the value of I(0), the small is the estimated R₀. By the stringent definition of R₀, we must consider I(0) = 1. However, the initial condition I(0) > 1 mimics the first case of covid-19 occurring earlier than the time t = 0. The Singapore University of Technology and Design [8] estimated R₀ using I(0) = 100 for different countries.

2 The elaborated model

One of the main aspects of covid-19 is increased lethality in elder individuals. For this reason, a population is divided into two groups, composed of young (60 years old or less, denoted by subscript y), and elder (60 years old or more, denoted by subscript o) individuals. The vital dynamic of this community is described by the per-capita rates of birth (ϕ) and mortality (μ), and φ is the aging rate, that is, the flow from young subpopulation y to elder subpopulation o.

Since we are dealing with the initial phase of the epidemic, the model is that presented in [7], but the compartments related to quarantine and mass testing are removed. Hence, for each subpopulation j (j = y, o), individuals are divided into six classes: susceptible S_j, exposed and incubating E_j, asymptomatic A_j, symptomatic persons in the initial phase of covid-19 (or prediseased) D_1j, and symptomatic persons with severe covid-19 D_2j, mild covid-19 Q_2j. However, all young and elder individuals in classes A_j, Q_2j, and D_2j enter into the same immune class I (this is the 7^th class, but common to both subpopulations).

The natural history of new coronavirus infection is the same for young (j = y) and elder (j = o) subpopulations. We assume that persons in the asymptomatic (A_j), pre-diseased (D_1j), and a fraction z_j of mild covid-19 (Q_2j) classes are transmitting the virus, and other infected classes ((1 − z_j) Q_2j and D_2j) are under voluntary or forced isolation. Susceptible persons are infected according to λ_jS_j (known as the mass action law [3]) and enter into class E_j, where λ_j is the per-capita incidence rate (or force of infection) defined by λ_j = λ (δ_jy + ψδ_jo), with λ being 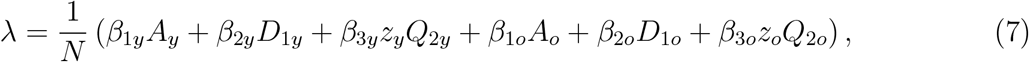where δ_ij is Kronecker delta, with δ_ij = 1 if i = j, and 0, if i ≠ j; and β_1j, β_2j and β_3j are the transmission rates, that is, the rates at which a virus encounters a susceptible people and infects him/her. After an average period 1/σ_j in class E_j, where σ_j is the incubation rate, exposed individuals enter into the asymptomatic class A_j (with probability p_j) or pre-diseased class D_1j (with probability 1 − p_j). After an average period 1/γ_j in class A_j, where γ_j is the recovery rate of asymptomatic individuals, asymptomatic individuals acquire immunity (recovered) and enter into immune class I. Possibly asymptomatic individuals can manifest symptoms at the end of this period, and a fraction 1 − χ_j enters into mild covid-19 class Q_2j. For symptomatic persons, after an average period 1/γ_1j in class D_1j, where γ_1j is the infection rate of pre-diseased individuals, pre-diseased individuals enter into severe covid-19 class D_2j (with probability 1 − m_j) or class Q_2j (with probability m_j). Individuals in class D₂ acquire immunity after period 1/γ_2j, where γ_2j is the recovery rate of severe covid-19, and enter into class I or die under the disease-induced (additional) mortality rate α_j. Individuals in class Q_2j acquire immunity after period 1/γ_3j, where γ_3j is the recovery rate of mild covid-19, and enter into immune class I.

The new coronavirus transmission model is described by the system of ordinary differential equations, with j = y, o. Equations for susceptible individuals are 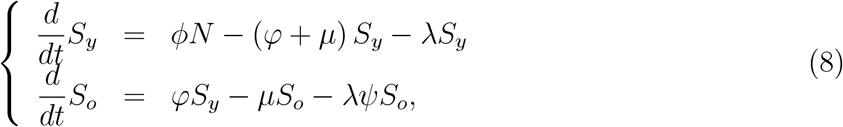for infectious individuals, and for immune individuals, where N_j = S_j + E_j + A_j + D_1j + Q_2j + D_2j, and N = N_y + N_o + I obeys 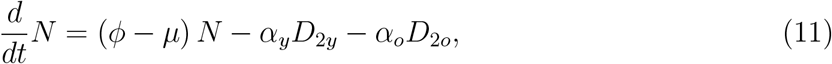with the initial number of population at t = 0 being N (0) = N₀ = N_0y + N_0o, where N_0y and N_0o are the size of young and elder subpopulations at t = 0. If ϕ = μ+(α_yD_2y + α_oD_2o) /N, the total size of the population is constant. The accumulated severe covid-19 cases Ω is obtained from 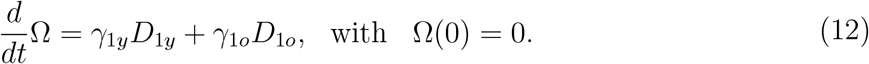Table 2 summarizes the model parameters. The description of the assigned values can be found in [7]. The transmission and additional mortality rates are estimated.

The basic reproduction number R₀ for the system of equations (8), (9) and (10) written in terms of the corresponding fractions is 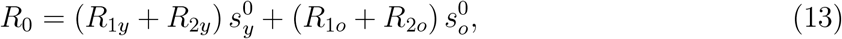where and Details of calculations can be found in [7].

To estimate the transmission rates, we consider β_y = β_1y = β_2y = β_3y and β_o = β_1o = β_2o = β_3o = ψβ_y, and we use equation (6) and Ω given by equation (12). The values for the model parameters are those given in Table 1. The basic reproduction number R₀ is calculated using equation (13).

The initial conditions supplied to the system of equations (8), (9) and (10) are, for young and elder subpopulations, 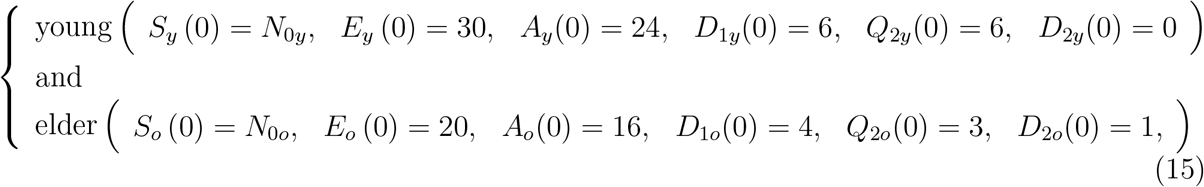plus I(0) = 0, where the initial simulation time t = 0 corresponds to the calendar time when the first case was confirmed (February 26 for São Paulo State, and January 31 for Spain). For São Paulo State, N_0y = 37.8 million and N_0o = 6.8 million, and for Spain, N_0y = 35.17 million and N_0o = 12.23 million.

For the data collected from São Paulo State, we obtained R₀ = 9.24, with Sum = 1.22×10⁶, while for the data collected from Spain, we obtained R₀ = 8.0, with Sum = 5.8 × 10⁸. If we let z_y = z_o = 0 (mild covid-19 cases do not transmit) and χ_y = χ_o = 1 (asymptomatic individuals do not relapse to mild covid-19), the estimated basic reproduction number is R₀ = 8.72 for São Paulo State, with Sum = 1.23 × 10⁶, and R₀ = 7.35 for Spain, with Sum = 1.59 × 10⁸.

3 Discussion and conclusion

Firstly, in the elaborated model, there are several infectious classes but the severe covid-19 cases do not transmit the SARS-CoV-2, for this reason, R₀ does not depend on the additional mortality rates α_y and α_o (see equations (13) and (14)). On the other hand, in the SIR model, there is only one infectious class, and R₀ depends on the additional mortality rate α (see equation (A.2)).

As we have pointed out, at the beginning and also in the early phase of the covid-19 epidemic, only hospitalized severe covid-19 cases were registered after confirmed by serological or PCR test. These individuals are either isolated in hospitals (receiving treatment) or discharged from hospitals but recommend to be isolated in their home. Then, somehow, the majority of these individuals are not participating in the populational SARS-CoV-2 chain transmission. In the SIR model, the unique way to estimate the transmission rate is considering that severe covid-9 cases are forming the infective class I. Hence, the estimation of R₀ provided by the SIR model using severe covid-19 cases is unrealistic.

There are different manners to define an epidemic curve. For instance, one possible definition is the curve formed by those positive for serological and PCR tests. However, in the early phase of (natural) epidemic, the covid-19 epidemic curve must be defined by severe cases, which are the only available data. In the elaborated model, the covid-19 epidemic curve was retrieved by estimating the transmission rates of asymptomatic, pre-diseased, and a fraction of mild classes. The estimated basic reproduction number was higher than that usually accepted: R₀ = 9.24 for São Paulo State, and R₀ = 8.0 for Spain. The usually accepted estimation of R₀ is around 3 obtained from the SIR model, which results from the estimated transmission rate of the severe covid-19 class. In [9], it was shown that the ratio between non-apparent and apparent covid-19 is around 24, showing that SARS-CoV-2 is being transmitted by a huge number of hidden cases. In the elaborated model, the initial conditions E(0) = 50 and I(0) = 1 were supplied to the dynamical system, resulting in R₀ = 9.24 (São Paulo State) and R₀ = 8.0 (Spain). Instead of comparing with the SIR model, let us compare with the SEIR model considering the same initial conditions E(0) = 50 and I(0) = 1 supplied to the elaborated model (see Appendix B). The estimated basic reproduction number for São Paulo State was R₀ = 3.92, and for Spain, R₀ = 4.41.

Comparing SIR, SEIR, and elaborated model, as the model incorporates more aspects of the natural history of the infection, higher becomes the estimation of R₀. For SIR and SEIR models, there is not any alternative except considering severe covid-19 cases as infective. However, in the elaborated model, the asymptomatic (A), pre-diseased (D₁) and a fraction of mild covid-19 (Q₂) individuals are transmitting SARS-CoV-2, but the severe covid-19 (D₂) individuals are isolated and do not contribute, except to the hospital staff [9].

As we have pointed out, the estimation of R₀ is important because this number determines the magnitude of effort to eradicate infection. In [7], describing the lockdown in Spain, they argued that if R₀ = 3, at least 67% of the population must be isolated to control the epidemic, while for R₀ = 8, at least 87% of the population must be isolated. They showed that 70% of the population in lockdown did not explain the covid-19 data in Spain, but 90% of the population in lockdown explained better the observed data.

With respect to the SIR model, Li et al. [10] explicitly cited that, by using data from January 10 to February 8, 2020, they estimated the effective reproduction number R_ef instead of R₀, arguing that the most recent common ancestor could have occurred on November 17, 2019. The time elapsed from November 17, 2019 (the first case) to January 10, 2020 (the first day in the estimation) is 54 days. However, on January 23, 2020, Wuhan and other cities of Hubei province imposed a rigid lockdown, sowing that they estimated R₀ taking also into account data recorded 16 days after the lockdown. In other words, they used the severe covid-19 data from 54 after the possible first case to 16 days after the implementation of a rigid lockdown (January 10 to February 8).

We conclude that the SIR model is not appropriate to estimate the basic reproduction number R₀, specifically in the case of the covid-19 epidemic when the severe covid-19 cases may not transmit SARS-CoV-2 populationally. Elaborated models taking into account important aspects related to the natural history of the infection estimate more accurately R₀. For instance, the incorporation of the asymptomatic individuals, the pre-diseased individuals, different lethality according to age, for instance, to improve the mathematical model.

A Steady-state analysis of the SIR model

The system of equations (1) does not reach steady state, except if ϕ = μ + αI/N. However, the system (1) in term of fractions attains steady state [7]. Defining the fraction x = X/N, with X = {S, I, R}, we have 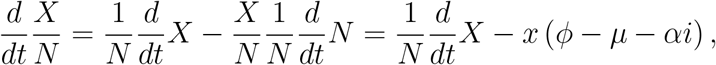using equation (2), and the system of equations (1) becomes 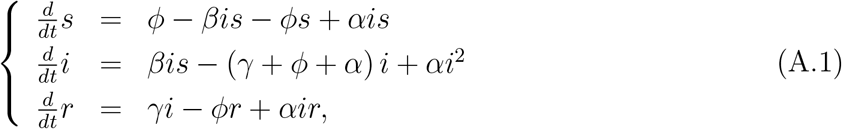with s + i + r = 1, hence, the equation for r can be decoupled from the system, through r = 1 − s − i. Notice that d (s + i + r) /dt = 0, and the system of equations in terms of fractions attain a steady state.

The system of equations (A.1), dropping out the decoupled equation for r, has two equilibrium points: The trivial (disease-free) equilibrium point and non-trivial (epidemic) equilibrium point .

The Jacobian matrix J evaluated at the trivial equilibrium point is 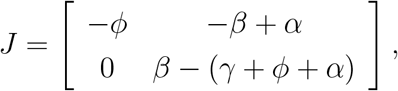with eigenvalues ρ₁ = −ϕ and ρ₂ = (γ + ϕ + α) (R₀ − 1), where the basic reproduction number R₀ is given by Hence, P⁰ is locally asymptotically stable if R₀ < 1.

The non-trivial equilibrium point has the coordinates given by where i* is the positive root but small than one of the second degree polynomial P₂(i) given by 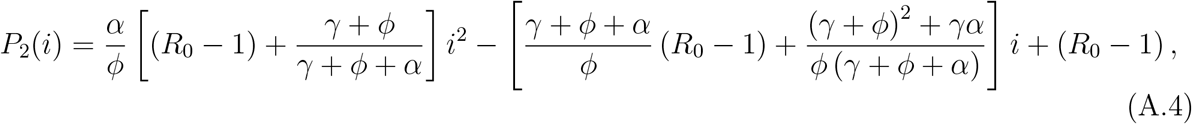which has the value, at i = 1, 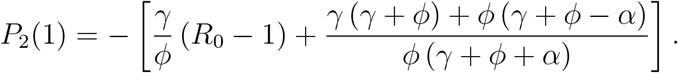When R₀ > 1, we have P₂(1) < 0 (the condition γ + ϕ > α is satisfied once γ > α), and the two positive roots of P₂(i) are such that . Hence the small root 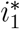is biologically feasible. When R₀ = 1, we have and , hence 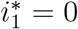is biologically feasible. When R₀ < 1, we have 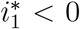and , hence 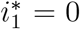is biologically feasible. Therefore, the small root , which is biologically feasible, assumes a negative value for R₀ < 1, zero at R₀ = 1, and positive value but lower than 1 for R₀ > 1. The small root of P₂(i) is given by 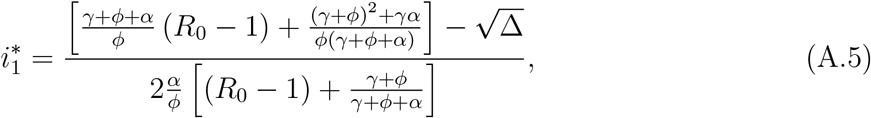where Δ is 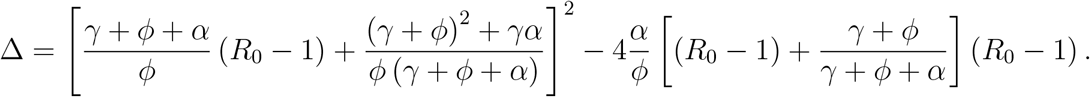The complexity arises due to the non-constant population under the additional mortality rate. Let us consider α = 0. In this case, P₂(i) has a unique positive solution and the fraction of susceptible individuals, from equation (A.3), is When α > 0, comparing equations (A.3) and (A.5), we notice that s* has a complex dependency with R₀, not simply 1/R₀.

B The SEIR model

Including the exposed class E in the SIR model, we have the SEIR model 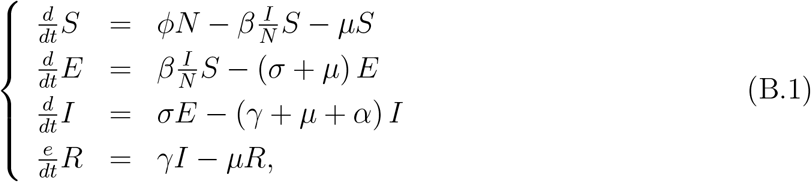where σ is the incubation rate. As the previous analysis for the SIR model, we can obtain the basic reproduction number R₀, which is given by when ϕ = μ, and the accumulated cases Ω obeys To estimate R₀ for the elaborated model in the main text, we used as the initial conditions E(0) = 50 and I(0) = 1 among others. For SEIR model, let us consider as the initial conditions E(0) = 50 and I(0) = 1, but S(0) and R(0) are the same supplied to the SIR model. We let σ = 1/5.8 days⁻¹ (elaborated model), and the values for other parameters are those provided in the SIR model. The value γ = 1/10 days⁻¹ in somehow considered an average value among γ, γ₁, γ₂ and γ₃ in the elaborated model. The estimated basic reproduction number for Sao Paulo State was R₀ = 3.92 with Sum = 1.29 × 10⁶, and for Spain, R₀ = 4.41 with Sum = 2.24 × 10⁸.

Notice that σ/ (σ + μ) = 0.99999, hence, R₀ given by equations (A.2) and (B.2) must be equal if β is the same. However, β is estimated by the dynamical systems (1) or (B.1) against the accumulated severe covid-19 cases. For this reason, the estimated β must be different between SIR and SEIR models. Let us consider SEIR model considering the initial conditions S(0) = N₀, E(0) = 0, R(0) = 0, and varying I(0).

For the data collected from São Paulo State, with S(0) = 44.6 million, we obtained for I(0) = 1, R₀ = 7.84 with Sum = 1.11 × 10⁶, for I(0) = 10, R₀ = 5.1 with Sum = 4.52 × 10⁵, for I(0) = 25, R₀ = 4.02 with Sum = 1.21 × 10⁶, and for I(0) = 100, R₀ = 2.74 with Sum = 3.51 × 10⁶. The lowest Sum occurs when R₀ = 5.1.

For the data collected from Spain, with S(0) = 47.4 million, we obtained for I(0) = 1, R₀ = 6.86 with Sum = 7.01×10⁸, for I(0) = 10, R₀ = 5.1 with Sum = 7.79×10⁸, for I(0) = 25, R₀ = 4.46 with Sum = 9.54 × 10⁸, and for I(0) = 100, R₀ = 3.58 with Sum = 1.33 × 10⁹. The lowest Sum occurs when R₀ = 6.86.

Comparing with the estimated R₀ provided by the SIR model (see the main text), we observe that SEIR model estimated with higher value. Let us assess the role played by E(0). We choose data from São Paulo State, letting I(0) = 10, S(0) = 44.6 million, R(0) = 0, and varying E(0) (for the SIR model, R₀ = 2.4). for E(0) = 1, R₀ = 5.03 with Sum = 4.57 × 10⁵, for E(0) = 10, R₀ = 4.61 with Sum = 6.19 × 10⁵, for E(0) = 25, R₀ = 4.13 with Sum = 9.86 × 10⁵, and for E(0) = 100, R₀ = 3.04 with Sum = 3.31 × 10⁶. The lowest Sum occurs when R₀ = 5.03, however, as E(0) increases, the estimated R₀ approaches to that provided by the SIR model.