Abstract
Imaging phenotypes extracted via radiomics of magnetic resonance imaging have shown great potential in predicting the treatment response in breast cancer patients after administering neoadjuvant systemic therapy (NST). Understanding the causal relationships between Imaging phenotypes, Clinical information, and Molecular (ICM) features, and the treatment response are critical in guiding treatment strategies and management plans. Counterfactual explanations provide an interpretable approach to generating causal inference; however, existing approaches are either computationally prohibitive for high dimensional problems, generate unrealistic counterfactuals, or confound the effects of causal features. This paper proposes a new method called Sparse CounteRGAN (SCGAN) for generating counterfactual instances to establish causal relationships between ICM features and the treatment response after NST. The generative approach learns the distribution of the original instances and, therefore, ensures that the new instances are realistic. Further, we propose a loss function that regularizes the counterfactuals to minimize the distance between original instances and counterfactuals (to promote sparsity) and the distances among generated counterfactuals to promote diversity. We evaluate the proposed method on two publicly available datasets, followed by the breast cancer dataset, and compare their performance with existing methods in the literature. Finally, we demonstrate the causal relationships from generated counter-factual instances. Results show that SCGAN generates plausible and realistic counterfactual instances with small changes in only a few features, making it a valuable tool for understanding the causal relationships between ICM features and treatment response.
1 Introduction
Breast cancer screening and diagnosis commonly use Magnetic Resonance Imaging (MRI), which has become a standard imaging tool for identifying individuals at risk of developing breast cancer and assessing the extent of cancer after initial diagnosis [1]. In combination with radiomics and machine learning, imaging techniques are becoming increasingly important in decision-making related to breast cancer treatment [2]. One such application is the use of MRI to predict the response of breast cancer patients to neoadjuvant systemic therapy (NST). Although NST was initially developed for patients with locally advanced breast cancer, it is now also used for those with early-stage cancer as it may lead to a pathologic complete response (pCR) [3]. Accurate prediction of pathologic response to NST could help avoid unnecessary surgical procedures, reduce treatment costs, and minimize side effects [4]. However, determining the suitability of NST for a patient before surgery can be complex and depends on various factors, including patient demographics, tumor characteristics, clinical history, and molecular subtypes [5].
Several machine learning models, e.g., decision trees [6] and deep learning [7], have emerged to predict the pathologic response of breast cancer patients to NST using pre-operative dynamic contrast-enhanced (DCE)-MRI [8, 9]. However, these models lack interpretability, making it difficult to understand the influence of different features such as imaging phenotypes, clinical information, and molecular (ICM) features on the prediction of pathologic response. As a result, the wider applicability of these models in clinical decision-making is limited. To address this issue, several models for generating explanations from black-box machine learning models have been proposed, such as LIME (Local Interpretable Model-agnostic Explanations) [10, 11], and Shapley values [12]. These methods estimate the average feature contributions to making a particular prediction by recording changes in the model’s predictions when adding or removing a feature. However, these models only capture the correlation between features and response and not necessarily their causal relationships.
Studying causal inference is important for two main reasons. First, correlation does not imply causation and, therefore, cannot provide a basis for decision-making [13]. Second, understanding the causal relationships between ICM features and pCR after NST may lead to opportunities for targeted therapies and help oncologists and patients make informed decisions about continuing or limiting systemic therapy after initial consultation [14]. In a recent publication, Pearl et al. [15] argued that counterfactual explanations could provide the highest level of interpretability in machine learning models and serve as a basis for generating causal inferences. Counterfactual explanations are a type of explanation that attempts to answer the question about an alternate reality. For instance, “What would have happened if X had been observed differently?” In other words, they provide an explanation of how the outcome of an event or decision might have changed if some of the input variables or features had been different [16]. Ideally, counterfactuals should have as few features as possible differently expressed to isolate the effect of causal factors [17]. For instance, in the context of predicting pathologic response, counterfactual explanations could uncover how the expression of ICM features might differ if a patient had achieved pCR instead of a pathological non-complete response (pNR). The counterfactual analysis provides a framework to estimate the causal effect of an intervention or a factor by comparing the observed outcome to the outcome observed under alternate interventions or different factor values [18].
Various techniques for generating counterfactual explanations have been developed, including model-agnostic [19], model-specific [20], and adversarial methods [21]. However, they have some critical limitations in generating realistic and sparse instances. For instance, model-agnostic methods, such as Diverse Counterfactual Explanations (DiCE) [19] require minimization of a multi-objective loss function using a gradient descent algorithm for optimization that is computationally costly, limiting their applicability to low-dimensional problems. Furthermore, optimization methods tend to generate more unrealistic counterfactuals. Adversarial models such as CounteRGAN (CGAN) [21] overcome the challenges of optimization-based model-agnostic methods by learning the distribution of data samples in high-dimensional spaces, therefore, avoiding unrealistic counterfactuals. A downside of restricting counterfactuals to the original data distribution is that a large number of features are changed simultaneously, confounding the true causal effects. In contrast, changing too few features may be insufficient to alter the class label of the original instance, failing to generate the counterfactuals. Finally, the plausibility and diversity of the generated counterfactuals remain critical limitations of the existing methods, which ensure the generated counterfactuals are logically reasonable and not similar, as plausibility limits the number of mutable features while diversity requires the model to suggest a wide range of change [22]. The generated counterfactuals instances should satisfy plausibility, while also balancing diversity and proximity to the original input [19].
The current paper builds on our initial work on generating causal inferences in predicting breast cancer treatment response from ICM features [23]. Our approach employed DiCE to generate counterfactuals. However, due to the computational cost of DiCE, we preselected the top 10 features using Shapley values to generate the counterfactual instances [23]. Limiting the feature space significantly limited the ability of our method to investigate the feature space that comprised 536 features (see Section 4.3). This paper overcomes the limitation and extends our initial work by proposing a generative approach called Sparse CounteRGAN (SCGAN) to generate counterfactuals from the original feature space. Figure 1 shows the architecture of SCGAN. In particular, we introduce a loss function inside CGAN that simultaneously minimizes the distance between original instances and counterfactuals and maximizes the distances among the generated counterfactuals, promoting both sparsity and diversity. Through numerical experiments, we observe that our approach outperforms existing methods, such as DiCE and CGAN, in generating counterfactual instances with minimal feature changes while maintaining feature value distribution and diversity.
The SCGAN method on an example of breast cancer MR image. The MR image is segmented to identify specific structures of interest such as the breast tissue and tumor. Tabular feature information is then extracted from the segmented regions, and used as input to the CGAN method. CGAN uses three neural networks: a generator, a discriminator, and a classifier. The generator produces residuals that, when added to the input, generate a realistic counterfactual instance. The generated counterfactual instance is then fed back to the generator to encourage diversity.
The rest of the paper is organized as follows. Section 2 introduces the concept of counterfactuals and the existing counterfactual generation models. In Section 3, we explain the details of our proposed counterfactual generation framework. Section 4 presents the experimental results of our proposed method on three realistic datasets and compares its performance with two existing counterfactual generation methods. We also use the proposed method to extract causal relationships between breast cancer treatment response and ICM features. Finally, Section 5 summarizes our contributions and provides directions for future research.
2 Background and Related Work
Counterfactual refers to a statement or situation that describes an alternative outcome or event that could have occurred but did not actually happen [16, 18]. In other words, it is a hypothesis or conjecture about what could have happened in the past or present if certain conditions or actions had been different. In machine learning, counterfactuals are hypothetical instances similar to observed instances but with minimal changes to features that are deemed causal [16, 18]. The purpose of generating counterfactual examples is to explore what-if scenarios and to understand the relationship between input features and the output of a machine learning model. We gain insights into how changing certain features might affect the model’s prediction by generating counterfactual instances and, thereby, identifying the features that affect the decision of a class.
Many methods have been proposed to generate counterfactuals, including using random feature permutations and incorporating different criteria in the loss functions to consider more properties [19, 24], modeling counterfactual generation as a constraint satisfaction problem [25], using genetic algorithms as the optimization method to search for counterfactuals [26], generating explanations by using Shapley values [27], generating explanations by using the weights of a regression model with LIME as the underlying framework [28], and using probabilistic models to find the nearest counterfactuals [29]. Despite the diversity of methods, their ultimate goal is to generate meaningful and plausible counterfactuals that can shed light on the causal relationships between input features and model predictions.
Chou et. al have proposed a set of criteria that should be met in order to generate counterfactuals that are interpretable. These properties include proximity, plausibility, sparsity, diversity, and feasibility [22]. Specifically, the concept of proximity is essential during the generation of a counterfactual explanation as it involves computing the distance between the input data point and the counterfactual [30]. The plausibility of a counterfactual explanation is also a key requirement, which states that the generated counterfactuals must be valid, and the search process should ensure logically reasonable results [30]. This means that a desirable counterfactual should avoid changing immutable features such as gender or race, as these changes are not plausible in real-world scenarios. The concept of sparsity pertains to the approaches employed to efficiently determine the minimum set of features that must be modified to produce a counterfactual explanation [31]. By satisfying this criterion, counterfactual explanations become more effective, comprehensible, and interpretable to humans. The diversity property in counterfactual explanation generation acknowledges that solely concentrating on proximity can result in generating counterfactual explanations that are very similar, with only minor variations between them. As such, diversity has been introduced as a technique to generate a set of diverse counterfactual explanations for the same instance [19, 25]. This approach leads to more interpretable and comprehensible explanations for users. Feasibility addresses the concern that identifying the nearest counterfactual to an instance may not result in a feasible modification of the features [32]. It stipulates that a generated counterfactual explanation should be practically achievable in the real world.
Despite the various properties that an ideal counterfactual generation algorithm should possess, we found that most existing algorithms are only able to achieve some of these properties. For instance, WatcherCF [24], one of the first algorithms for generating model-agnostic counterfactuals, only includes proximity and sparsity terms in its loss function. DiCE [19], an extension and improvement of WatcherCF, adds an additional diversity term in the loss function and achieves plausibility by adding a constraint to immutable features. However, feasibility is not guaranteed, so the generated counterfactuals may not always be realistic. In addition to these algorithms, Multi-Objective Counterfactual Explanations (MOCE) proposed by Dandl et al. [26] translates the counterfactual search into a multi-objective optimization problem based on genetic algorithms. However, this algorithm also cannot guarantee both plausibility and feasibility. There are other algorithms that incorporate more properties by adding constraints or using probabilistic models, but generating realistic counterfactuals remains a challenge. A detailed review of counterfactual generation can be found in [22].
Applying counterfactual explanations for causal inference in the medical field is particularly meaningful because of the high stakes involved in medical decision-making. Medical decisions can have serious consequences for patients, and it is essential that clinicians have a thorough understanding of the potential outcomes associated with different treatment options. Counterfactual explanations can provide a deeper understanding of the causal relationships between various medical factors, helping clinicians to make more informed decisions. In our recent work, Zhou et al. [23] propose a DiCE-based method for identifying causal relationships between imaging phenotypes, clinical information, molecular features, and treatment response in breast cancer patients. The authors compare their approach to traditional explanation methods, such as LIME and Shapley, and highlight the advantages of the counterfactual approach. However, due to the computational complexity of DiCE, the authors use Shapley values to filter out the top 10 most important features for further analysis. It is worth noting that, as Fernandez et al. [33] have shown, a high importance weight from Shapley is not always sufficient for a feature to be part of a counterfactual explanation. Therefore, the use of Shapley for dimensionality reduction should be considered as an alternative heuristic approach.
Due to the challenges of generating high-quality counterfactuals that satisfy the various introduced properties and definitions, recent studies have turned to explore the potential of Generative Adversarial Networks, or GANs, as a viable option for this task [21]. GANs have been widely used in the field of image generation and have shown impressive results in generating realistic images [34]. GANs can generate samples from a complex data distribution by training a generator network to generate samples that are similar to the real data distribution while training a discriminator network to distinguish between real and generated samples. The idea of using GANs for generating counterfactual explanations stems from the fact that counterfactuals can be thought of as alternative samples from a similar data distribution. By training a GAN on the original data, we can generate counterfactuals that are both similar to the original data and satisfy the desired properties of counterfactuals, such as proximity, plausibility, sparsity, diversity, and feasibility.
By incorporating the principles and criteria for producing high-quality counterfactuals, Nemirovsky et al. [21] proposed a counterfactual explanation framework CGAN. This framework is specifically designed to generate counterfactuals that are both meaningful and feasible in achieving the intended goal while remaining realistic, actionable, and computationally efficient. In addition to the generator and discriminator networks, CGAN also includes a classifier network. The role of the classifier is to provide additional supervision during training by classifying the original and counterfactual examples into different categories. In CGAN, a regularization term is used to encourage sparsity, which is a combination of L1 and L2. In CGAN, immutable features are features that cannot be modified or changed, such as the age or gender of a person. In such cases, CGAN applies counterfactual search with no modifications to these immutable features and simply cancels out the perturbations applied to these features during the generation of the counterfactual instance. However, this approach may lead to unrealistic or uninterpretable counterfactual explanations if the immutable features are highly influential in determining the predicted outcome.
Based on the literature review, it is clear that generating counterfactual instances has gained significant attention for interpreting machine learning models and establishing causal relationships. However, most existing methods have limitations in generating realistic and sparse instances, hindering their applicability in the real-world context. In this paper, we propose a novel method called SCGAN that addresses these limitations by using a GAN-based framework to generate counterfactual instances that are both sparse and realistic while promoting proximity and diversity. We evaluate our proposed method on three real-world datasets, demonstrating its ability to extract causal relationships between imaging phenotypes, clinical information, molecular features, and treatment response in breast cancer patients.
3 Methodology
3.1 CounterGAN
The idea behind GANs is to create two neural networks, a generator and a discriminator, that are trained together in a competitive process. The generator learns to generate new data that looks like the input data, while the discriminator learns to distinguish between the real input data and the generated data. During training, the generator tries to generate data that will fool the discriminator into thinking it is real, while the discriminator tries to distinguish between the real and generated data. As the generator gets better at generating realistic data, the discriminator gets better at distinguishing between the real and generated data, and the two networks continue to improve in a back-and-forth process. Once the training is complete, the generator can be used to generate new data that is similar to the input data.
CGAN extends standard GANs to generate counterfactuals that address common issues, including mode collapse (failure to capture the full diversity of training data) and limited sparsity and proximity [21]. During the training process, the generator network generates residuals that are added to the original instance to produce a counterfactual instance. The discriminator network tries to distinguish the counterfactual instance from the original instance. The classifier network then classifies the original and counterfactual examples into different categories, such as “positive” and “negative”. This additional supervision helps to ensure that the generator network produces counterfactual instances that are not only plausible but also meaningful in terms of the classification task.
The overall objective function of CGAN is expressed as:
where G is the generator network, D is the discriminator network, C is the classifier network, L(G, D) is the Residual GAN loss, and Lc(G, C) is the classification loss. Reg(G) is the regularization term. During the training process, the generator network aims to minimize the loss function while the discriminator network aims to maximize the same loss function. The Residual GAN loss L(G, D) in CGAN is formulated as:
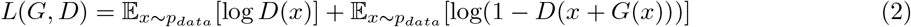where x is an instance from the original dataset, and G(x) is a generated residual for achieving counterfactual. x + G(x) is the generated counterfactual instance. In this setup, both the generator and discriminator take input from the original dataset. In the absence of any other constraints, the generator may generate null residuals since the input is already real data. However, the other two terms Lc(G, C) and Reg(G) guide the generator to generate instances that also satisfy the counterfactual requirement and the regularization requirement.
The classification loss Lc is formulated as:
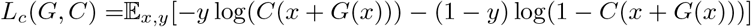where x represents an original instance, y is the corresponding label, and C(x +G(x)) denotes the output of the classifier network for the generated counterfactual instance. The classification loss measures the binary cross-entropy between the output of the classifier network for the generated counterfactual instance and the opposite label (i.e., 1−y). By minimizing this loss, CGAN ensures that the generated instances have the desired counterfactual properties while also being classified accurately by the classifier network. The regularization term Reg(G) promotes additional properties for the generated counterfactual instances. In the CGAN proposed in [21], the regularization term is formulated as a combination of L1 and L2 regularization, which enables control over both sparsity and feature perturbations, shown as:
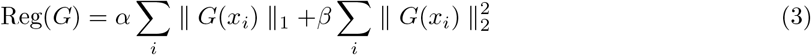where xi is an instance drawn from the entire data distribution.
The L1 regularization encourages sparsity, meaning that only a small subset of features will be changed in each generated instance, while the L2 term controls the magnitude of feature perturbations.
3.2 Sparse CounteRGAN
One potential limitation of using a combination of L1 and L2 regularization is that the relative strengths of the two regularization terms must be manually specified. This can be a difficult task and may require tuning via trial and error. Additionally, there may not be a clear theoretical justification for choosing a specific combination of L1 and L2 regularization. In this paper, we modify the regularization term to include a p-norm regularization. With p-norm regularization, we can set the value of p to control the sparsity of the solution, where a larger value of p corresponds to a more sparse solution with fewer changed features. Specifically, the p-norm of an original instance x and counterfactual c with Nf features is defined as:
By using a p-norm regularization term, where p can be any value, we can customize the regularization to better suit the specific characteristics of our data and the task at hand. This approach can be particularly useful when dealing with high-dimensional or noisy data. Additionally, a p-norm regularization term can help balance the trade-off between sparsity and smoothness, providing a more flexible and effective way to regularize the GAN training.
In addition to the p-norm term, the regularization term Reg(G) is augmented with a diversity term in our proposed method.
where X is the training batch, S is the pre-defined set of reference counterfactual instances, dist(cx, s) measures the distance between generated counterfactual cx for the original instance x and pre-defined counterfactual s. For a new instance for which we haven’t generated counterfactuals before, the S is an empty set. Each time we generate a new counterfactual instance, the generated counterfactual instance will also be added to S to encourage diversity for future counterfactuals.
Specifically, the distance dist(cx, s) is defined as
This term penalizes the generator for producing instances that are similar to the pre-defined set of instances to promote diversity in the generated samples. In a counterfactual generation, diversity is important because it helps to generate multiple plausible explanations for a given input instance. For example, if we want to generate counterfactual instances for a person who was denied a loan, there could be several reasons why the loan was denied, and each reason may correspond to a different counterfactual instance. By generating diverse instances, we can explore these different possible explanations and provide more options for decision-making. The new Reg(G) is expressed as:
where λ1 and λ2 are used to balance the importance of the sparsity and diversity.
To achieve plausibility by handling immutable features that cannot be modified, such as age or gender, we used a mask method to restrict the set of features that can be changed in a generated instance. The mask method creates a vector mask consisting of binary values that indicates which features can be changed and which ones cannot. The original method used in CGAN cancels the perturbations applied to immutable features, which may not be ideal when these features are causally related to the outcome of interest. In contrast, the mask method we used provides more flexibility in handling immutable features. By creating a binary mask, we can specify which features are mutable and which ones are immutable and therefore have more control over the generation of counterfactual instances. This approach can be particularly useful in scenarios where certain features have a strong causal relationship with the outcome and cannot be changed. Furthermore, the mask method enables the use of a wider range of regularization techniques to control the extent of feature changes, which can improve the quality and interpretability of the generated counterfactual instances.
Moreover, the mask method allows us to limit the maximum number of features that can be changed. During training, we allow the model randomly select the mutable features that the number of features equal to the maximum allow-to-change number, and set the corresponding entries in the mask to 1. All other entries in the mask are set to 0, indicating that those features cannot be changed. Applying the mask during training ensures that only the allowed number of features are modified, which controls the number of changed features and prevents the generator from making too many changes, resulting in unrealistic instances.
In binary classification problems, the output of a classifier is typically a probability value indicating the likelihood of an instance belonging to one of the two classes. However, in counterfactual generation, it is necessary to make a binary decision based on this probability value. This decision is often made by applying a threshold value to the classifier probability. If the probability value is greater than or equal to the threshold, the instance is classified as belonging to one class, and if the probability value is less than the threshold, the it is classified as belonging to the other class. The choice of threshold value can significantly affect the classification performance, as a high threshold will lead to a conservative classifier that is less likely to make false positive errors, but more likely to make false negative errors, while a low threshold will lead to an aggressive classifier that is less likely to make false negative errors, but more likely to make false positive errors. By default, the threshold is set as 0.5 in this paper.
In small datasets, a well-trained discriminator encourages the model to generate instances that closely resemble the original data, but lack diversity and proximity to the counterfactual instances. To address the challenge of CGAN in balancing the generation of realistic and counterfactual instances, we modified the discriminator in the original CGAN model to be less sensitive to fake instances. Specifically, we increase the dropout rate [35] and reduce the number of neurons in the layers to encourage the model to explore a wider range of feature values, thereby ensuring minimal feature changes while qualifying as realistic instances.
3.3 Evaluation Metrics
We evaluate our method using four metrics. First, we evaluate the class of the generated instance. Second, we evaluate the classifier prediction probability of the generated instances. We accept a generated instance as a counterfactual if the corresponding prediction probability exceeds 0.5. A higher prediction probability indicates higher confidence in the classifier’s prediction. Third, we measure the sparsity by counting the number of features changed in the counterfactual instance from the original instance, and is defined as:
Fourth, we measure proximity, which is the distance between the original and the generated counterfactual instance. Specifically, we use the Euclidean distance d(c, x) shown below to measure the distance between the original instance x and the generated counterfactual instance c:
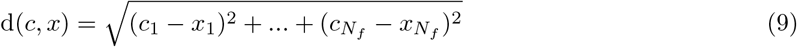
We want to generate counterfactuals with higher sparsity and lower proximity belonging to the class opposite to original instance with higher prediction probability.
4 Numerical Experiments
We conduct a comprehensive evaluation of our approach on three distinct datasets: the Pima Indians Diabetes dataset [36], the Ionosphere dataset [37], and the Breast Cancer DCE-MRI dataset [38]. We utilize a neural network binary classifier [39] to predict the classes of generated counterfactual instances, as well as to guide the generator in generating instances that align with the desired class.
We first evaluate our method starting with the Pima Indians Diabetes dataset [36], following the experiment in [21]. This dataset comprises eight features that describe relevant patient characteristics for predicting the presence of diabetes. The target label is positive if the patient has diabetes (268 instances) and negative otherwise (500 instances). The second dataset we use to evaluate our method is the Ionosphere dataset [37], which has 34 numerical features and binary classifications for radar returns from the ionosphere. “Good” radar returns (225 instances) are those showing evidence of some type of structure in the ionosphere. “Bad” returns (126 instances) are those that do not; their signals pass through the ionosphere. In this experiment, we compare three methods using randomly selected original instances where the radar returns are classified as “Good” (class 0). Our objective is to generate instances that could lead to “Bad” returns (class 1). We finally apply our method to the open-source pre-operative DCE-MRI data from Saha et al. [38], which extracted 529 radiomic features for 922 breast cancer patients diagnosed with invasive breast cancer between January 2000 to March 2014. These radiomic features characterize the size, shape, texture, and enhancement of both the tumor and the surrounding tissues in 2D as well as 3D. Along with radiomic features, we also considered four features pertaining to patient demographics: date of birth (days), menopausal status (at diagnosis), race and ethnicity, metastatic at presentation (outside of lymph nodes), and three features representing the tumor characteristics: estrogen receptor (ER), progesterone receptor (PR), and human epidermal growth factor receptor 2 (HER2). For each of the patients, the pathologic response to NST is recorded. Among the 922 patients, 288 patients are assessed for the neoadjuvant therapy status. Each of the responses belongs to one of the five classes: complete response, non-complete response, ductal carcinoma in situ only remaining, lobular carcinoma in situ only remaining, and treatment response assessment unavailable. To simplify the model, we only considered the patients that belonged to pCR and pNR. The data statistics show that 64 patients achieved pCR and the remaining 224 belonged to the pNR class.
For the numerical experiments in this paper, we split the dataset into training and test sets using stratified sampling to ensure a balanced distribution of the target label. Specifically, we assign 80% of the dataset to the train set and the remaining 20% to the test set. Table 1 shows the classifier performance across all four cases (two benchmarks and one case study) for testing data. All experiments are run on a DELL Precision 7865 Tower with AMD Ryzen Threadripper PRO 5945WX 12-core processor and 128 GB RAM.
Comparison of Classifier Performance
4.1 Benchmark 1 Pima Indians Diabetes
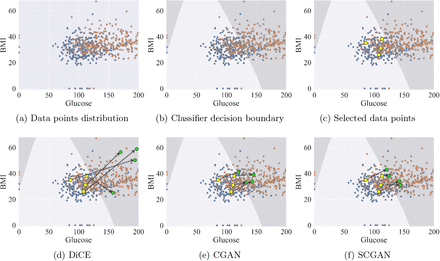
We first visually illustrate the generation of counterfactual instances with different methods, i.e., DiCE, CGAN, and SCGAN. Figure 2(a) shows a scatter plot between glucose concentration (x-axis) and BMI (y-axis) measurements for the Pima Indians. Figure 2(b) shows the decision boundary of the binary classifier. We select four points (shown in yellow in Figure 2(c) representing patients without diabetes to generate the corresponding counterfactuals. The counterfactuals should provide meaningful recourse to transform these patients into realistic-looking patients with diabetes. The counterfactuals generated by DiCE (shown in Figure 2(d)) require a significant change in both glucose and BMI. We also notice that some of the counterfactuals lie near or outside the boundary of the original data, making them less likely to be realistic. Using CGAN (as shown in Figure 2(e)), the generated counterfactuals are more realistic and require smaller changes to features, but necessitate altering both features in all cases. The proposed SCGAN method (as seen in Figure 2(f)) results in counterfactuals that achieve the desired classification and only require changes to one feature in two examples, making it more interpretable for causal inference in diabetes diagnosis.
Comparison of three counterfactual search techniques on the Pima Indians Diabetes dataset, showing how they achieve their objectives while generating markedly different counterfactual instances.
For the Pima Indians Diabetes dataset, we considered the features Pregnancies, Age, and Diabetes Pedigree Function as immutable, while Glucose, Insulin, Body Mass Index, Tricept Skin Fold Thickness, and Blood Pressure are treated as mutable, as suggested in [21]. To achieve plausibility by limiting the changes made to the immutable features during counterfactual generation, we employ the mask method that created a binary mask specifying which features could be changed and which could not.
In this experiment, we compare three methods using randomly selected original instances where the patients who have no diabetes are classified as “negative” (class 0). Our objective is to generate instances that belong to the “positive” return class (class 1). We generate 50 counterfactual instances for each of the five initial instances and summarize the average performance in Table 2. For the CGAN method, l1 and l2 are coefficients of L1 and L2 regularization terms, respectively. To make a fair comparison, we set p = 1 in our method, which means the L1 norm is used. Thus, l1 and λ1 control the weight of the L1 regularization term in CGAN and SCGAN respectively. The CF% column in the table summarizes the percentage of generated counterfactual instances that achieve the opposite classification. The next three columns show the average measurements of the classifier probability, sparsity, and proximity metrics for all initial instances. For CF% and classifier probability, higher values indicate better performance, while for sparsity and proximity metrics, lower values are indicative of better counterfactuals.
Model Performance Comparison for Benchmark 1
All three methods generated counterfactual instances with opposite classifier predictions for most instances. DiCE is significantly faster than the other two methods and achieves counterfactuals for more than 95% of generated instances by changing on average 2.1 features. However, the average confidence level of the generated instances is lower than the counterfactuals produced by SCGAN, and the proximity (amount of change) is much larger than both CGAN and SCGAN. In contrast, SCGAN with λ1 = 1 generated counterfactuals with better sparsity (number of changes) and achieved a higher average confidence level than the other two methods. When comparing the last two rows with different λ1 values for SCGAN, we observe that a smaller λ1 value leads to less sparsity, which is as expected since the feature value differences are less penalized. However, the percentage of generated instances that achieve counterfactual and the confidence level of counterfactual instances are also higher. These results suggest that SCGAN provides a promising approach for generating counterfactual explanations.
Figure 3 displays the feature value distribution of BMI in the Pima Indians Diabetes dataset and the feature values of generated counterfactual instances. The histogram represents the distribution of the entire dataset and vertical lines represent the individual instances. We observe that the counterfactuals generated via DiCE are diverse but lie near the tail of the original data distribution, suggesting that such instances are less likely to be realistic. On the other hand, CGAN and SCGAN generate counterfactual instances with the BMI values located in a high-density region, making them more realistic. In comparison to CGAN (green line), the counterfactual instances generated from SCGAN (blue lines) are more diverse.
The feature value distribution of BMI in the Pima Indians Diabetes dataset. The histogram shows the distribution of values in the entire dataset. Vertical lines depict the original and counterfactual instances generated by DiCE, CGAN, and SCGAN, color-coded as per the legend.
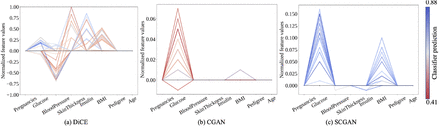
Figure 4 visualizes the counterfactual instances generated by DiCE, CGAN, and SCGAN for a selected initial instance. The counterfactuals are color-coded per their prediction probability, with blue closer to 1 (more likely) and red close to 0.5 (less likely). We see that DiCE generates counterfactual instances with large changes and low confidence levels compared to CGAN and SCGAN. CGAN’s counterfactuals have fewer feature changes than DiCE but lack diversity. In contrast, SCGAN produces diverse counterfactual instances and achieves good confidence levels for most counterfactual instances. For both CGAN and SCGAN, generated counterfactual instances show less diversity than DiCE. However, considering the result shown in Figure 3, both CGAN and SCGAN consider the feasibility requirement, while the diverse counterfactuals from DiCE may not be realistic.
Counterfactual instances generated by three methods. The horizontal axis represents the features and the vertical axis represents the normalized feature values. The black zero line represents the actual instance. Every counterfactual instance has either one or more changes in the feature values, each of which is color-coded based on their classification probability.
Our numerical experiments on the Pima Indians Diabetes dataset have shown that glucose and BMI are the two features that are most frequently changed. These results conclude that glucose and BMI are the primary causal factors in diabetes diagnosis. This conclusion is also in line with the findings of previous studies [40].
4.2 Benchmark 2 Ionosphere
We conduct experiments similar to benchmark 1 by setting p = 1 in our method and generating 50 counterfactuals for each initial instance. The average performance of the three methods is summarized in Table 3. DiCE is the fastest method and generates counterfactuals by changing fewer than 6 features on average for tested instances. However, the average confidence level of the generated instances is not as high as those produced by SCGAN, and the proximity measurement is much larger than both CGAN and SCGAN. On the other hand, SCGAN is able to find more counterfactual instances than CGAN and achieves high confidence levels for the generated counterfactuals. When comparing SCGAN with different λ1 values, we observed that a weaker regularization term produced counterfactual instances with higher confidence levels but required more changes in features as a trade-off.
Model Performance Comparison for Benchmark 2
Figure 5 displays the feature value distribution of Attribute 12 in the Ionosphere dataset and the feature values of generated counterfactual instances. We note that DiCE is the only method that generated a counterfactual instance with a feature value above 1, which is beyond the range of the feature value distribution in the dataset. This indicates that the generated counterfactual instances from DiCE could be unrealistic. SCGAN generated counterfactual instances with feature values distributed in a wider range than CGAN, indicating diversity.
The feature value distribution of Attribute 12 in the Ionosphere dataset. The histogram shows the distribution of values in the entire dataset. Vertical lines depict the original and counterfactual instances generated by DiCE, CGAN, and SCGAN, color-coded as per the legend.
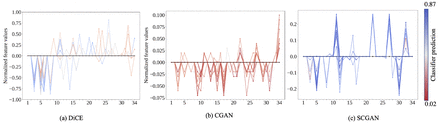
Figure 6 displays the counterfactual instances generated by DiCE, CGAN, and SCGAN for a selected initial instance. The color-coded lines indicate the normalized feature values of the generated counterfactual instances by each method, where red colors represent low confidence levels (probability away from 1) and blue colors mean high confidence levels (probability close to 1). A careful observation of the figure reveals that DiCE generates counterfactual instances with large changes compared to the other two methods. CGAN, on the other hand, generates instances with small changes but with poor confidence levels for most generated instances. SCGAN, however, changes the features at moderate levels and guarantees high confidence levels and diversity.
Counterfactual instances generated by three methods. The horizontal axis represents the features and the vertical axis represents the normalized feature values. The black zero line represents the actual instance. Every counterfactual is represented as a color-coded line, where the color is based on classification probability.
The Ionosphere dataset has 34 attributes to describe 17 pulse numbers obtained from the complex electromagnetic signal collected by a system in Goose Bay, Labrador [37]. Based on the results from SCGAN, we observe that the 25th and 27th attributes are the primary contributing factors to the identification of the “Good” radar signals from the bad ones.
4.3 Case Study: Breast Cancer DCE-MRI
We generated 50 counterfactual instances for each initial instance and summarized the average results in Table 4. For this particular instance, CGAN is unable to generate counterfactual instances with opposite classifier predictions in more than thirty percent of the generated instances. Our proposed method, SCGAN, demonstrates higher confidence in generating counterfactual instances than the CGAN. SCGAN also achieves better sparsity (number of changed features) with the same L1 setting. In addition, we observe that a stronger regularization term for SCGAN produces counterfactual instances with lower confidence levels but required fewer changes in features, as shown in the last two rows of Table 4. This trade-off highlights the importance of carefully tuning the regularization coefficient to balance between sparsity and confidence levels in generating meaningful and accurate counterfactual instances. DiCE is unable to generate any counterfactual instances for a single patient within the time limit of one hour.
Model Performance Comparison for Breast Cancer DCE-MRI Dataset
Figure 7 illustrates the distribution of “similar clustered tumor proportion” in the Breast Cancer dataset and the feature values of generated counterfactual instances. Our proposed method, SCGAN, generates counterfactual instances with feature values more diverse and from a higher data density region compared to CGAN. This characteristic of our method demonstrates its ability to generate counterfactual instances that are more realistic, which is beneficial for causal inference.
The feature value distribution of the similar clustered tumor voxel proportion in the Breast Cancer dataset. The histogram shows the distribution of values of the feature in the entire dataset. Vertical lines depict the original and counterfactual instances generated by CGAN, and SCGAN, color-coded as per the legend.
After comparing our results with those in [23], we found that our proposed SCGAN method is unable to generate counterfactual instances with only one feature change, using the model built over all 536 features. However, it is worth noting that the 10-feature model used in [23] was much simpler than our current model and therefore may not have captured all the relevant factors that contribute to the predicted outcome. In contrast, our SCGAN model is more complex and takes into account interactions between multiple features, making the resulting counterfactuals more realistic. However, it is possible that our model is overfitting to the training data, given that the dataset contains only 288 data points while there are 536 features. Therefore, we should be cautious when generalizing results to new examples outside the training set.
Based on the original Breast Cancer dataset, we use correlation and collinearity to filter out 41 features for the case study to improve the performance and interpretability of the classifier. Highly correlated features lead to overfitting and reduce the generalization power of the model [41]. Collinear features, on the other hand, add redundant information, which increases the complexity of the model [42]. By removing these redundant and highly correlated features, we improve the efficiency, accuracy, and interpretability of our model. Specifically, we calculate the correlation matrix and look for features with a high correlation coefficient. If a pair of features have a high correlation coefficient (> 0.85), then one of them is dropped. Secondly, the variance inflation factor (VIF) is calculated for each feature to assess the degree of collinearity. Features with a high VIF (> 10) indicate high collinearity and are dropped.
In this case, we have a relatively small number of categorical features (three), and to avoid any loss of information due to rounding, we employ a method that compares both close categories when these features are suggested to be changed, instead of the general rounding way [21]. Specifically, we test both categories and select the one that resulted in higher confidence for the classifier prediction. By doing so, we ensure that the counterfactual generated is as close as possible to the opposite response, while still being valid in terms of the classifier prediction. In this case, despite using the 41 features, DiCE is unable to generate any counterfactual instances for a single patient within the time limit of one hour.
We generated 50 counterfactual instances for each initial instance and summarize the average performance in Table 5. Overall, SCGAN generated more counterfactual instances than CGAN, showing higher confidence in the generated counterfactual instances. The Avg Prox column shows that SCGAN has a much larger value than CGAN, caused by the changes in categorical features. Upon observing the generated counterfactual instances, we find that CGAN does not change categorical features as they are treated the same as numerical features, merely using a general rounding step to assign categories. As a result, the effects of categorical features are eliminated in most scenarios, even when they significantly impact the outcome. This makes it harder for the model to find a counterfactual with high confidence. On the other hand, our proposed method is able to handle categorical features by comparing both close categories to test for the classifier prediction, ensuring that the categorical information is retained and the model generates more counterfactual instances with higher confidence.
Model Performance Comparison for Reduced Breast Cancer DCE-MRI Dataset
From the generated counterfactual instances, we have observed that only three out of the 41 filtered ICM features are involved in generating all the counterfactual instances, namely PR status (which stands for progesterone receptors status), the HER2 status (where HER2 is a protein that helps breast cancer cells to grow rapidly), and the variance of uptake (which captures the inhomogeneity of IV uptake between successive MRI frames), which is consistent with the previous finding in the breast cancer literature [43]. These features are considered causal features for predicting the treatment response in breast cancer. This information is extremely helpful in guiding oncologists to optimize decision-making in breast cancer treatment. For instance, for a patient who is unable to achieve pCR, the above three features can be emphasized to increase the likelihood of achieving pCR. Furthermore, additional counterfactual explanation analysis can be conducted to extract features with a high impact for certain patients. For instance, when a specific patient has counterfactual instances that change PR status all the time, it indicates that we can increase the probability of realizing pCR by changing the PR status in the specific patient which originally could not achieve pCR. This is significant as it would allow oncologists to administer hormone therapy to block PR-positive tumors by using estrogen and/or progesterone prior to administering the tumor. This is just one example of counterfactual explanation. Depending on their feasibility, healthcare professionals may employ different counterfactual explanations to increase the likelihood of achieving pCR following NST.
5 Conclusions
In this paper, we extend the CGAN approach to generating counterfactual instances that are sparse and diverse to achieve causal inference and overcome the computational limitations of DiCE. Our method introduces a new loss function with regularization terms to minimize distances among generated counterfactuals and between original instances and counterfactuals, a new mask strategy to handle immutable features, and an increased dropout rate to encourage the model to explore a wider range of feature values when the dataset size is too small. We evaluate our method on three publicly available datasets, including a breast cancer dataset, and compare its performance with DiCE and CGAN. The results demonstrate that SCGAN generates plausible and realistic counterfactual instances with small changes in only a few features, making it a valuable tool for understanding the causal relationships between pathologic response to NST and ICM features which included imaging phenotypes, clinical history, and molecular features. By performing counterfactual analysis, we identified cause-and-effect relationships between breast MR imaging phenotypes, molecular features and pathologic response to NST.
Further research is required to improve the efficiency and scalability of the method without retraining the model and better methods for handling categorical features. Tuning the coefficients of the regularization terms is a potential direction for future research to balance accuracy and sparsity in generating counterfactual instances.
Data Availability
All data produced in the present study are available upon reasonable request to the authors.
Acknowledgments
The authors are grateful for the kind support provided by the Gerstner Family and the Brandt Young Scholarship from the Centers of Individualized Medicine and ASU-Mayo Clinic Summer residency program.
References
