Abstract
The COVID-19 epidemic started in the Hubei province in China in December 2019 and then spread around the world reaching the pandemic stage at the beginning of March 2020. Since then, several countries went into lockdown. We estimate the effect of the lockdown in France on the contact rate and the effective reproduction number Re of the COVID-19. We obtain a reduction by a factor 7 (Re = 0.47, 95%-CI: 0.45-0.50), compared to the estimates carried out in France at the early stage of the epidemic. We also estimate the fraction of the population that would be infected by the beginning of May, at the official date at which the lockdown should be relaxed. We find a fraction of 3.7% (95%-CI: 3.0-4.8%) of the total French population, without taking into account the number of recovered individuals before April 1st, which is not known. This proportion is seemingly too low to reach herd immunity. Thus, even if the lockdown strongly mitigated the first epidemic wave, keeping a low value of Re is crucial to avoid an uncontrolled second wave (initiated with much more infectious cases than the first wave) and to hence avoid the saturation of hospital facilities. Our approach is based on the mechanistic-statistical formalism, which uses a probabilistic model to connect the data collection process and the latent epidemiological process, which is described by a SIR-type differential equation model.
1 Introduction
COVID-19 epidemic started in the Hubei province in China in December 2019 and then spread around the world reaching the pandemic stage at the beginning of March 2020 [1]. To slow down the epidemic, several countries went into lockdown with different levels of restrictions. In the Hubei province, where the lockdown has been set long before the other countries (on January 23), the epidemic has reached a plateau, with only sporadic new cases by April 15 (from the data of Johns Hopkins University Center for Systems Science and Engineering [2]). In France, the first cases of COVID-19 were detected on January 24, and the lockdown has been set on March 17.
The basic reproduction number R0 corresponds to the expected number of new cases generated by a single infectious case in a fully susceptible population [3]. Several studies, mostly based on Chinese data, aimed at estimating the R0 associated with the COVID-19 epidemic, leading to values from 1.4 to 6.49, with an average of 3.28 [4]. As the value of R0 can be interpreted as the product of the contact rate and of the duration of the infectious period, and since the objective of the lockdown and associated restriction strategies are precisely to decrease the contact rate, an important effect on the number Re of secondary cases generated by an infectious individual is to be expected. This value Re is often referred to as ‘effective reproduction number’, and corresponds to the counterpart of R0 in a population that is not fully susceptible [5]. If Re > 1, the number of infectious cases in the population follows an increasing trend, and the larger Re, the faster this trend. On the contrary, if Re < 1, the epidemic will gradually die out. The study [6] showed that containment policies in Hubei province indeed led to a subexponential growth in the number of cases, consistent with a decrease in the effective reproduction number Re.
Standard epidemiological models generally rely on SIR (Susceptible-Infected-Removed) systems of ordinary differential equations and their extensions (for examples of application to the COVID-19 epidemic, see [7, 8]). With these models, and more generally for most deterministic models based on differential equations, when the loss of observation due to the observation process is heavy, specific approaches have to be used to bridge the gap between the models and the data. One of these approaches is based on the mechanistic-statistical formalism, which uses a probabilistic model to connect the data collection process and the latent variable described by the ODE model. Milestone articles and textbook have been written about this approach or related approaches [9], which is becoming standard in ecology [10, 11]. The application of this approach to human epidemiological data is still rare.
In a previous study [12], we applied this framework to the data corresponding to the beginning of the epidemic in France (from February 29 to March 17), with a SIR model. Our primary objective was to assess the infection fatality ratio (IFR), defined as the number of deaths divided by the number of infected cases. As the number of people that have been infected is not known, this quantity cannot directly measured, even now (on April 15). The mechanistic-statistical framework allowed us to compute an IFR of 0.8% (95%-CI: 0.45-1.25%), which was consistent with previous findings in China (0.66%) and in the UK (0.9%) [13] and lower than the value previously computed on the Diamond Princess cruse ship data (1.3%) [14]. In this previous study, we also computed the R0 in France, and we found a value of 3.2 (95%-CI: 3.1-3.3). Although the number of tests at that stage was low, an advantage of working with the data from the beginning of the epidemic was that the initial state of the epidemic was known.
Here, we develop a new mechanistic-statistical approach, based on a SIRD model (D being the dead cases compartment), in the aim of
estimating the effect of the lockdown in France on the contact rate and the effective reproduction number Re;
estimating the number of infectious individuals and the fraction of the population that has been infected by the beginning of May (at the official date at which the lockdown should be relaxed).
2 Materials and Methods
2.1 Data
We obtained the number of positive cases and deaths in France, day by day from Santé Publique France [15], from March 31 to April 14. We obtained weekly data on the number of individuals tested (in private laboratories and hospitals) from the same source. We assumed that during each of these weeks the number of tests per day was constant. This assumption is consistent with the small variations between the number of tests during the first week (111 690) and the second week of observation (132 392). As the data on the number of positive cases are not fully reliable (fewer cases during weekends with a rebound on Monday), we smoothed the data with a moving average over 5 days. Official data on the number of deaths by COVID-19 since the beginning of the epidemic in France only take into account hospitalised people. About 728 000 people in France live in nursing homes (EHPAD, source: DREES [16]). The number of deaths in these structures has only been reported recently, and cannot be obtained day by day. Latest data from Santé Publique France indicate a total number of 10 643 deaths at hospital and 6 524 deaths in nursing homes by April 15. The total number of deaths therefore corresponds to about 1.6 times the number of deaths at hospital. The same factor had been estimated in [12] based on local dataset in the French Grand Est region.
2.2 Mechanistic-statistical framework
The mechanistic-statistical framework consists in the combination of a mechanistic model that describes the epidemiological process, a probabilistic observation model and an inference procedure.
2.2.1 Mechanistic model
The dynamics of the epidemic are described by the following SIRD compartmental model:
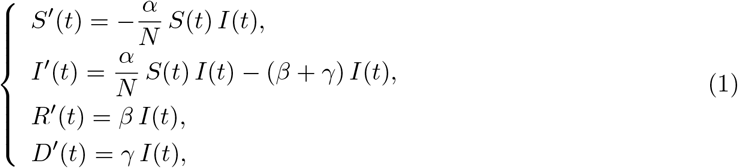with S the susceptible population, I the infectious population, R the recovered population, D the number of deaths due to the epidemic and N the total population. For simplicity, we assume that N is constant, equal to the current French population, thereby neglecting the effect of the small variations of the population on the coefficient α/N. The parameter α is the contact rate (to be estimated) and 1/β is the mean time until an infectious becomes recovered. Based on the results in [17], the median period of viral shedding is 20 days, but the infectiousness tends to decay before the end of this period: the results in [18] show that infectiousness starts from 2.5 days before symptom onset and declines within 7 days of illness onset. Based on these observations we assume here that 1/β = 10 days. The parameter γ corresponds to the death rate of the infectious (to be estimated).
Initial conditions
The model is started at a date t0 corresponding to April 1st. The initial number of infectious I(t0) = I0 is not known and will be estimated. The total number of recovered at time t0 is also not known. However, as the compartment R has no feedback on the other compartments, we may assume without loss of generality that R(t0) = 0, thereby considering only the new recovered individuals, starting from the date t0. We fixed D(t0) = 3523, the number of deaths at hospital by March 31. The initial S population at the beginning of the period, should still be close to the total French population: by March 31 only 52 128 cases had been observed in France, corresponding to 0.08% of the total population. A factor 8 had been estimated in [12] between the cumulated number of observed cases and the actual number of cases at the beginning of the epidemic. Even though this factor may have changed, e.g. increased by a factor 5, this means that the proportion of the total population that has been infected by March 31 is still small. We may assume any value for S(t0) between 60 106 and 67·106 without changing much the results of our study (as S/N remains close to 1). For our computation, we assumed that S(t0) = 66·106, corresponding to about 98.5% of the French population.
Numerical method
The ODE system (1) was solved thanks to a standard numerical algorithm, using Matlab® ode45 solver.
2.2.2 Observation model
The number of cases tested positive on day t, denoted by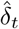 
, is modelled by independent binomial laws, conditionally on the number of tests nt carried out on day t, and on pt the probability of being tested positive in this sample:
The tested population consists of a fraction of the infectious cases and a fraction of the susceptibles: nt = τ1(t) I(t) + τ2(t) S(t). Thus,
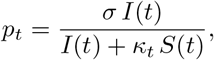with κt := τ2(t)/τ1(t), the relative probability of undergoing a screening test for an individual of type S vs an individual of type I. We assumed that the ratio κ was independent of t over the observation period. The coefficient σ corresponds to the sensitivity of the test. In most cases, RT-PCR tests have been used and existing data indicate that the sensitivity of this test using pharyngeal and nasal swabs is about 63 − 72% [19]. We assumed here σ = 0.7 (70% sensitivity).
Each day, the number of new observed deaths (excluding nursing homes), denoted by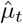 
, is modelled by independent Poisson distributions conditionally on the process D(t), with mean value D(t) − D(t − 1) (which measures the daily increment in the number of deaths):
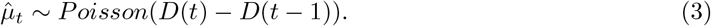
Note that the time t in (1) is a continuous variable, while the observations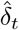 
and 
are reported at discrete times. For the sake of simplicity, we used the same notation t for the days in both the discrete and continuous cases. In the formulas (2) and (3) I(t), S(t) and D(t) are computed at the end of day t.
2.2.3 Statistical inference
The unknown parameters are α, γ, κ and I0. We used a Bayesian method [20] to estimate the posterior distribution of these parameters.
Computation of the likelihood function
The likelihood ℒ is defined as the probability of the observations (here, the increments 
) conditionally on the parameters. Using the observation models (2) and (3), and using the assumption that the increments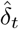 
and 
are independent conditionally on the underlying SIRD process and that the number of tests nt is known, we get:
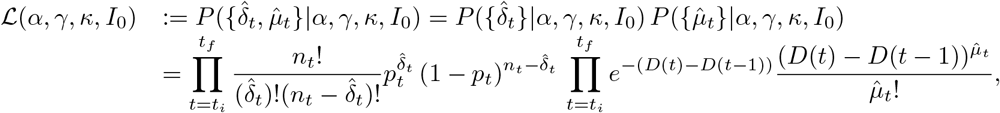with ti the date of the first observation and tf the date of the last observation. In this expression ℒ(α, γ, κ, I0) depends on α, γ, κ, I0 through pt and D(t).
Posterior distribution
The posterior distribution corresponds to the distribution of the parameters conditionally on the observations:
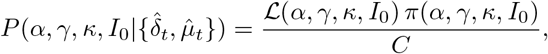where π(α, γ, κ, I0) corresponds to the prior distribution of the parameters (detailed below) and C is a normalization constant independent of the parameters.
Prior distribution
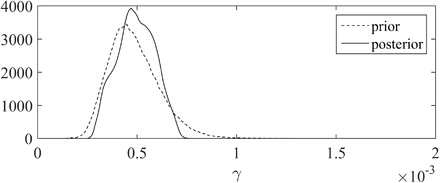
Regarding the contact rate α, the initial number of infectious cases I0 and the probability κ, we used independent non-informative uniform prior distributions in the intervals α ∈ (0, 1), I0 ∈ (1, 107) and κ ∈ (0, 1). To overcome identifiability issues, we used an informative prior distribution for γ. This distribution, say fg, was obtained in [12] during the early stage of the epidemic (fg is depicted in the Appendix, Fig. S1). In [12], the number of infectious cases I0 at the beginning of the epidemic was known (equal to 1), and did not need to be estimated. Thus, we estimated in [12] the distribution of the parameter γ by computing the distribution of the infectious class and using the formula D′(t) = γ I(t) together with mortality data (which were not used for the estimation of the other parameters, unlike in the present study). Finally, the prior distribution is defined as follows:
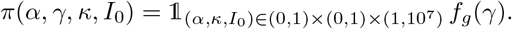
The numerical computation of the posterior distribution is performed with a Metropolis-Hastings (MCMC) algorithm, using 5 independent chains, each of which with 106 iterations, starting from the posterior mode. To find the posterior mode we used the BFGS constrained minimisation algorithm, applied to − ln(ℒ) − ln(π), via the Matlab ® function fmincon. In order to find a global minimum, we applied this method starting from 4000 random initial values.
3 Results
Model fit
Denote by 
the posterior mode, and S*(t), I*(t), R*(t), D*(t) the solutions of the system (1) associated with these parameter values. The observation model (2) implies that the associated expected number of cases tested positive on day t is 
(expectation of a binomial) with
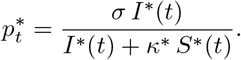
The observation model (3) implies that the expected cumulated number of deaths on day t is D*(t).
To assess model fit, we compared these expectations and the observations, i.e., the cumulated number of cases tested positive,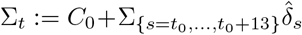
with C0 the number of cases tested positive by March 31 (C0 = 52 128) and the cumulated number of deaths 
, with M0 the number of reported deaths (at hospital) by March 31 (M0 = 3 123). The results are presented in Fig. 1. We observe a good match with the data.
The blue curve corresponds to the expected number of cases tested positive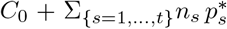 
given by the model, the red curve corresponds to the expected cumulated number of deaths D*(t) (excluding nursing homes). The crosses correspond to the observations (blue crosses: cumulated number of positive cases, red crosses: cumulated number of deaths). C0 is the number of cases tested positive on March 31 (C0 = 52 128).
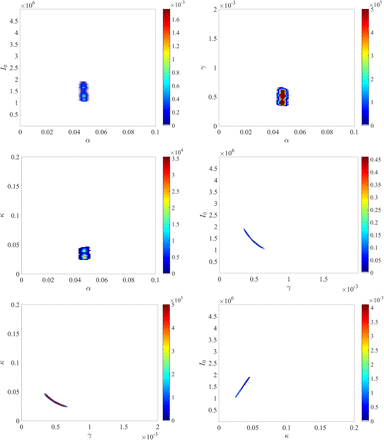
The pairwise posterior distributions of the parameters (α, I0), (α, γ), (α, κ), (γ, I0), (γ, κ), (κ, I0) are depicted in Appendix, Fig. S2. With the exception of the parameter γ (Fig. S1), for which we chose an informative prior, the posterior distribution is clearly different from the prior distribution, showing that new information was indeed contained in the data.
Contact rate and effective reproduction number
The effective reproduction number can be simply derived from the relation Re = α/β [3]. The distribution of Re is therefore easily derived from the marginal posterior distribution of the contact rate α (since we assumed β = 1/10; see Section 2.2). It is depicted in Fig. 2. We observe a mean value of Re of 0.47 (95%-CI: 0.45-0.50).
Dynamics of the infectious class
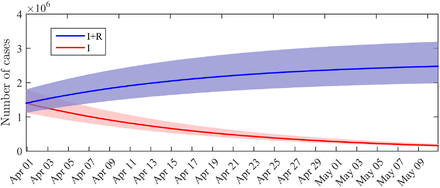
The marginal posterior distribution of I0 indicates that the number of infectious individuals at the beginning of the considered period (i.e. April 1st) is 1.4 · 106 (95%-CI: 1.1 · 106 − 1.8 · 106). The computation of the solution of (1) with the posterior distribution of the parameters leads to a number of infectious I(tf) = 7.0 · 105 and a total number of infected cases (including recovered) (I +R)(tf) = 2.0·106 at the end of the observation period (April 14). By May 10, if the restriction policies remain unchanged, we get a forecast of I(T) = 1.6 · 105 infectious cases (95%-CI: 1.3 · 105 − 2.1 · 105) and (I + R)(T) = 2.5 · 106 infected cases including recovered (95%-CI: 2.0 · 106 − 3.2 · 106). The dynamics of the distributions of I and I + R are depicted in
Fig. 3. By May 10, the total number of infected cases (including recovered) therefore corresponds to a fraction of 3.7% of the total French population. This value does not include the recovered cases before April 1st.
Solid lines: average value obtained from the posterior distribution of the parameters. Shaded areas: 0.025-0.975 interquantile ranges.
4 Discussion
Many studies focused on the estimation of the basic reproductive number R0 of the COVID-19 epidemic, based on data-driven methods and mathematical models (e.g., [21, 4]) describing the epidemic from its beginning. In average, the estimated value of R0 was about 3.3. We focused here on an observation period that began after the lockdown was set in France.
We obtained an effective reproduction number that was divided by a factor 7, compared to the estimate of the R0 carried out in France at the early stage of the epidemic, before the country went into lockdown (a value R0 = 3.2 was obtained in [12]). This indicates that the restriction policies were very efficient in decreasing the contact rate and therefore the number of infectious cases. In particular, the value Re = 0.47 is significantly below the threshold value 1 were the epidemic starts dying out.
The decay in the number of infectious cases can also be observed from our simulations. It has to be noted that, although the number of infectious cases is a latent, or ‘unobserved’ process, the mechanistic-statistical framework allowed us to estimate its value (Fig. 3). The cumulated number of infected cases that we obtained by May 10 (I + R) corresponds to a fraction of 3.7% (95%-CI: 3.0-4.8%) of the total French population, without taking into account the number of recovered individuals before April 1st, which is not known. Based on a value R0 = 3.2, the herd immunity threshold, corresponding to the minimum fraction of the population that must have immunity to stop the epidemic, would be 1 − 1/R0 ≈ 69% (a threshold of 80% was proposed in [22]). This proportion will probably not be reached by May 10. As emphasised by [23], a too fast relaxation of the lockdown-related restrictions before herd immunity is reached or efficient prophylaxis is developed), would expose the population to an uncontrolled second wave of infection. In the worst-case scenario, the effective reproduction number Re would approach the initially estimated value of R0, and the second wave would start with about 1.6 · 105 infectious individuals (in comparison with the few cases that initiated the first wave in France) and about 64 · 106 susceptible individuals. Keeping a low value of Re is therefore crucial to avoid the saturation of hospital facilities.
Data Availability
All data in the manuscript are available from opebn sources
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Author Contributions
L.R., E.K.K., J.P., A.S. and S.S. conceived the model and designed the statistical analysis. L.R. and S.S. wrote the paper, L.R. carried out the numerical computations. All authors reviewed the manuscript.
Funding
This work was funded by INRAE: MEDIA network.
Appendix
- The prior and marginal posterior distributions of the death rate γ are depicted in Fig. S1.
- The pairwise posterior distributions of the parameters (α, I0), (α, γ), (α, κ), (γ, I0), (γ, κ), (κ, I0) are depicted in Fig. S2.
