Abstract
The transmission of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) becomes pandemic but presents different incidences in the world. Mathematical models were formulated to describe the coronavirus disease 2019 (CoViD-19) epidemic in each country or region. At the beginning of the pandemic, many authors used the SIR (susceptible, infectious, and recovered compartments) and SEIR (including exposed compartment) models to estimate the basic reproduction number R0 for the CoViD-19 epidemic. These simple deterministic models assumed that the only available collection of the severe CoViD-19 cases transmitted the SARS-CoV-2 and estimated lower values for R0, ranging from 1.5 to 3.0. However, the major flaw in the estimation of R0 provided by the SIR and SEIR models was that the severe CoViD-19 patients were hospitalized, and, consequently, not transmitting. Hence, we proposed a more elaborate model considering the natural history of CoViD-19: the inclusion of asymptomatic, pre-symptomatic, mild and severe CoViD-19 compartments. The model also encompassed the fatality rate depending on age. This SEAPMDR model estimated R0 using the severe CoViD-19 data from São Paulo State (Brazil) and Spain, yielding higher values for R0, that is, 6.54 and 5.88, respectively. It is worth stressing that this model assumed that severe CoViD-19 cases were not participating in the SARS-CoV-2 transmission chain. Therefore, the SIR and SEIR models are not suitable to estimate R0 at the beginning of the epidemic by considering the isolated severe CoViD-19 data as transmitters.
1 Introduction
The first case of coronavirus disease 2019 (CoViD-19) was detected in China in December 2019 and spread rapidly to other countries. In March 2020, the World Health Organization (WHO) declared the CoViD-19 a pandemic. The CoViD-19 is caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), which can be transmitted by droplets that escape the lungs by coughing or sneezing and infects humans through the nose, mouth, or eyes. In severe cases, immune cells overreact, causing acute respiratory disease syndrome and possibly death.
At the beginning of the epidemic, we have two data sets: Severe CoViD-19 cases (those in hospitals were tested and confirmed) and deaths. Due to the lack of mass testing (PCR and serology), the epidemic curve consisted of severe CoViD-19 cases. Mathematical models, usually the SEIR (susceptible, exposed, infectious and recovered compartments) and the simplified SIR, were used to describe this epidemic curve. The model parameters were fitted to estimate the basic reproduction number R0.
In the literature, the usually estimated or assumed basic reproduction number R0 is around 2.0. For instance, Koo et al. [1] and Ferguson et al. [2] assumed R0 ranging between 1.5 and 2.6 and simulated agent-based models to predict the number of CoViD-19 cases and deaths. However, Li et al. [3], based on the SEIR-metapopulations model, estimated the effective reproduction number Ref considering data from January 10 to February 8, arguing that the most recent common ancestor could have occurred on November 17, 2019. The time elapsed from November 17, 2019 (the first case) to January 10, 2020 (the first day in the estimation) is 54 days. Moreover, on January 23, 2020, Wuhan and other Hubei province cities imposed a rigid lockdown. Hence, their estimation of Ref = 2.38 considered the range of data recorded from 54 days after the epidemic’s onset to 16 days after the lockdown. The definition of the basic reproduction number is “one infectious individual is introduced in a completely susceptible population without constraints (interventions)” [4]. Therefore, the estimation of R0 must consider the severe CoViD-19 data restricted on the period without interventions.
The estimation of the basic reproduction number R0 depends on the mathematical model [5]. To exemplify this dependency to describe the CoViD-19 epidemic, we consider the SIR and SEIR models, plus an additional model taking into account more compartments and encompassing the fatality rate depending on the age. The latter model divides a population into two subpopulations and split the infectious (I) compartment into asymptomatic (A), pre-diseased or pre-symptomatic (P), mild (M), and severe (D) CoViD-19 compartments. This model [6], called the SEAPMDR model, was proposed to show fewer deaths due to severe CoViD-19 cases than those provided by the SIR and SEIR models [2]. However, the SEAPMDR model estimated higher values for R0.
The reliable estimation of R0 is essential because this number determines the magnitude of effort to eradicate infection. For instance, a vaccination must immunize a fraction equal to or greater than 1 − 1/R0 of the susceptible population to eradicate a disease [4]. In [7], analyzing vaccination as a control mechanism, if Ref is reduced lower than one, the number of cases decreased following an exponential-type decay. Instead of vaccination, if we consider the isolation of susceptible individuals, for a lower value of R0 as provided by the SIR and SEIR models, a small fraction (1 − 1/R0) of the population must be in quarantine to control the transmission of SRS-CoV-2. However, the SEAPMDR model considering more details of the natural history of CoViD-19 estimated a higher value to R0, showing that the control is not an easy task.
As we have pointed out, only severe CoViD-19 cases were registered at the beginning of the epidemic. In the SIR and SEIR models, the collection of severe CoViD-19 data were allocated in the transmitting compartment I to estimate model parameters. However, in the SEAPMDR model, the observed data are allocated in the non-transmitting compartment D. Considering the severe CoViD-19 data collection from São Paulo State (Brazil) [8] and Spain [9], we fit the parameters of those models to calculate R0. We conclude that SIR and SEIR models are not suitable to estimate the basic reproduction number. For instance, the lower estimated values for R0 are a result of considering the data collected later after the beginning of the epidemic and data collected after the intervention (quarantine).
The paper is structured as follows. In Section 2, we describe SIR, SEIR, and SEAPMDR models used to estimate R0 in Section 3. Discussion is presented in Sections 4, and the conclusion in Section 5.
2 Material and methods
We present the SIR, SEIR, and SEAPMDR models in this section. From these models, we obtained R0 from the steady-state analysis.
2.1 The SIR and SEIR model
In the SEIR model, the population is divided into susceptible (S), exposed (E), infectious (I), and recovered (R) subpopulations (compartments). The population’s vital dynamics is described by the per-capita birth ϕ and natural mortality µ rates. In severe CoViD-19 cases, the overreacted immune cells may result in death described by the additional mortality (fatality) rate α.
According to the CoViD-19 natural history, susceptible individuals are infected at a rate λS, where the force of infection λ is given by
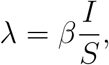with β being the transmission rate. After a period σ−1, where σ is the incubation rate, these individuals enter into infectious compartment and, after a period γ−1, where γ is the infectious (or recovery) rate, they enter into recovered compartment. Hence, the SEIR model is described by the dynamic system
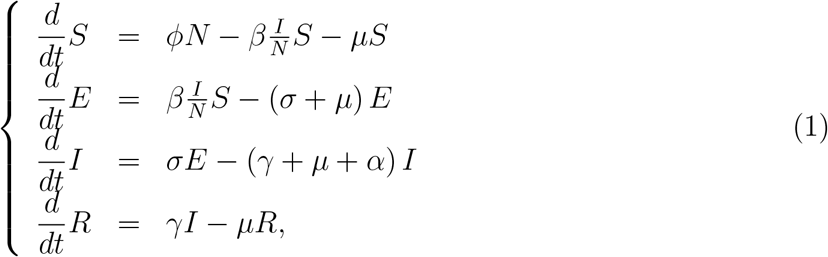where the total population N = S + E + I + R obeys
The number of accumulated severe CoViD-19 cases Ω is given by the exit from E and entering into class I, that is,
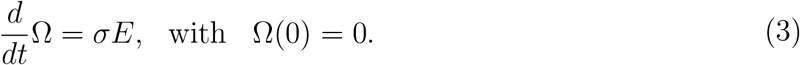and this equation is accopled to the system of equations (1) to obtain numerically Ω.
The system of equations (1) is autonomous but describes non-constant population dynamics (if ϕ = µ + αI/N, then N is constant). This varying population is the reason why the equation (1) can not be used directly to obtain the basic reproduction number. In Appendix A.1, the steady-state of the system of equations in terms of the fractions corresponding to equation (1) was analyzed to obtain the basic reproduction number R0.
The SIR model is obtained letting σ → ∞, resulting in
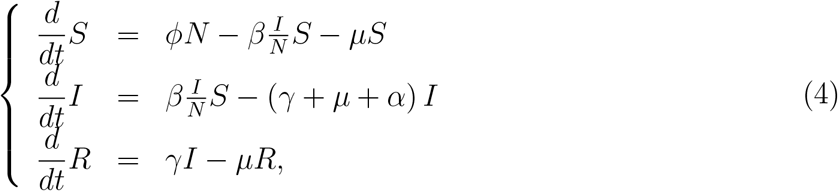and the number of accumulated severe CoViD-19 cases Ω is given by the exit from S and entering into class I, that is,
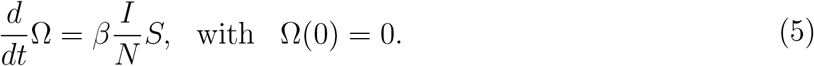
In Appendix A.2, the steady-state of the system of equations in terms of the fractions corresponding to equation (4) was analyzed to obtain the basic reproduction number R0.
2.2 The SEAPMDR model
One of the main aspects of CoViD-19 is increased fatality in the elder subpopulation. For this reason, a population is divided into two groups, composed of young (60 years old or less, denoted by subscript y) and elder (60 years old or more, denoted by subscript o) subpopulations. This community’s vital dynamic is described by the per-capita rates of birth (ϕ) and mortality (µ), and ϕ is the aging rate, that is, the flow from young subpopulation y to elder subpopulation o. Another aspect is the presence of the pre-symptomatic individuals, that is, individuals without symptoms transmitting SARS-CoV-2 before the onset of the disease [10].
Since we are dealing with the initial phase of the epidemic, the model does not consider the compartments related to quarantine and mass testing. Hence, for each subpopulation j (j = y, o), individuals are divided into six classes: susceptible Sj, exposed and incubating Ej, asymptomatic Aj, pre-symptomatic (or pre-diseased) individuals Pj, symptomatic individuals with mild CoViD-19 Mj, and severe CoViD-19 Dj. However, all young and elder individuals in classes Aj, Mj, and Dj enter into the same recovered class R (this is the 7th class, but common to both subpopulations). Hence, the SEAPMDR model has 13 compartments.
The natural history of CoViD-19 is the same for young (j = y) and elder (j = o) subpopulations. We assume that individuals in the asymptomatic (Aj), pre-diseased (Pj), and a fraction zj of mild CoViD-19 (Mj) classes are transmitting the virus. Other infected classes ((1 − zj) Mj and Dj) are under voluntary or forced isolation. Susceptible individuals are infected at a rate λjSj (known as the mass action law [4]), where λj is the per-capita incidence rate (or force of infection) defined by λj = λ (δjy + ψδjo), with λ being
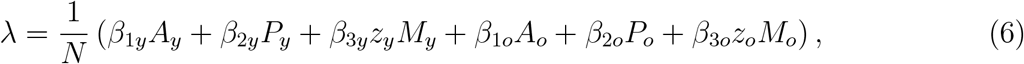where δij is the Kronecker delta, with δij = 1 if i = j, and 0, if i ≠ j; and β1j, β2j and β3j are the transmission rates, that is, the rates at which a virus encounters a susceptible people and infects him/her. In [6], a particular model was analyzed letting zy = zo = 0 and χy = χo = 1.
Susceptible individuals are infected at a rate λj and enter into class Ej. After an average period 1/σj in class Ej, where σj is the incubation rate, exposed individuals enter into the asymptomatic class Aj (with probability lj) or pre-diseased class Pj (with probability 1 − lj). After an average period 1/γj in class Aj, where γj is the recovery rate of asymptomatic individuals, asymptomatic individuals acquire immunity (recovered) and enter into recovered class R. Possibly asymptomatic individuals can manifest symptoms at the end of this period, and a fraction 1 − χj enters into mild CoViD-19 class Mj. For symptomatic individuals, after an average period 1/γ1j in class Pj, where γ1j is the infection rate of pre-diseased individuals, pre-diseased individuals enter into severe CoViD-19 class Dj (with probability 1 − kj) or mild CoViD-19 class Mj (with probability kj). Individuals in class Dj acquire immunity after a period 1/γ2j, where γ2j is the recovery rate of severe CoViD-19, and enter into recovered class R or die under the disease-induced (additional) mortality rate αj. Individuals in mild CoViD-19 class Mj acquire immunity after a period 1/γ3j, where γ3j is the recovery rate of mild CoViD-19, and enter into recovered class R.
The SARS-CoV-2 transmission model is described by the system of ordinary differential equations. Equations for susceptible individuals are
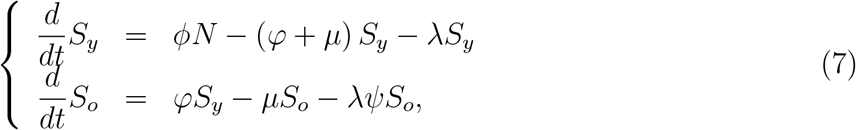for infectious individuals, with j = y, o,
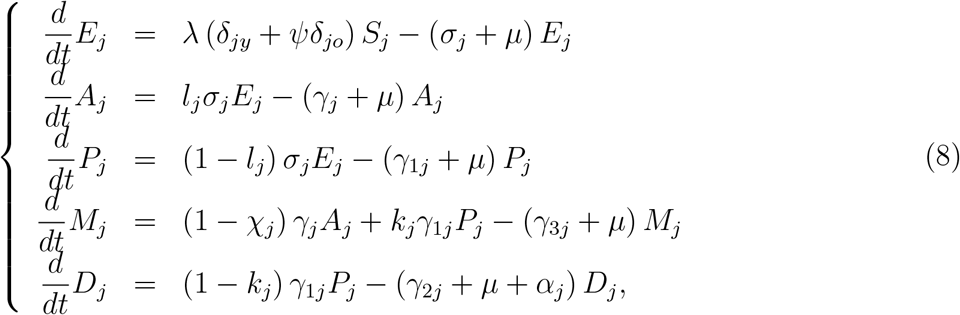and for recovered individuals,
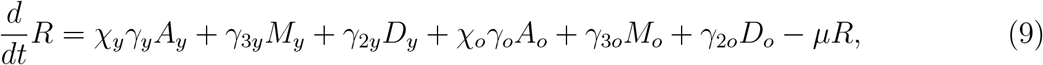where Nj = Sj + Ej + Aj + Pj + Mj + Dj, and N = Ny + No + I obeys
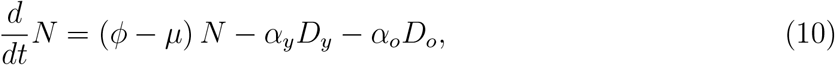with the initial number of population at t = 0 being N (0) = N0 = N0y + N0o, where N0y and N0o are the size of young and elder subpopulations at t = 0.
The number of accumulated severe CoViD-19 cases Ω is obtained from
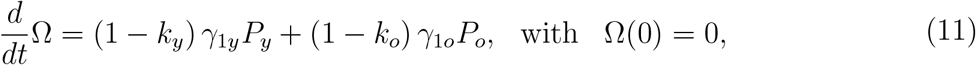which are the exit from class P, and entering into class D.
Table 1 summarizes the model parameters. The description of the assigned values can be found in [11]. The transmission rates are estimated.
Summary of the model parameters (j = y, o) and values (rates in days−1, and proportions are dimensionless). The values (∗) correspond to São Paulo State. For Spain, ϕ = µ = 1/(83.4 × 365) days−1, φ = 1.14 × 10−5 days−1, and ψ = 1.1.
In Appendix B, the steady-state of the system of equations in terms of fractions corresponding to equations (7), (8) and (9) was analyzed to obtain the basic reproduction number R0.
The basic reproduction number R0 given by equation (B.8) in Appendix B, with the fractions written as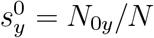 
and 
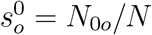, is
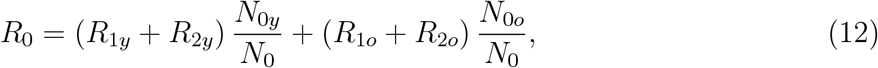where N0y and N0o are the initial numbers of young and elder subpopulations with N0 = N0y + N0o, and
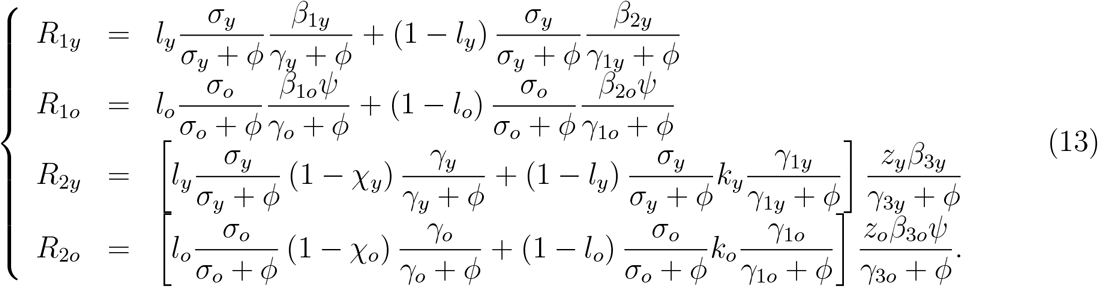
Letting zy = zo = 0 (R2y = R2o = 0), we retrieve the basic reproduction number obtained in [11].
2.3 The sigmoid-shaped curve of Ω
The first derivative of Ω is given by equations (5), (3) and (11) for, respectively, SIR, SEIR and SEAPMDR models, or
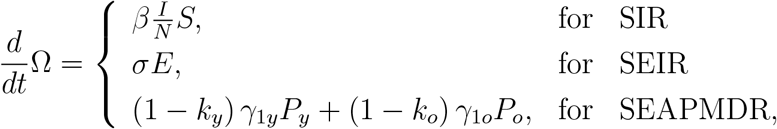which is positive (dΩ/dt > 0). Hence, Ω is monotonically increasing function.
The second derivative of Ω is given
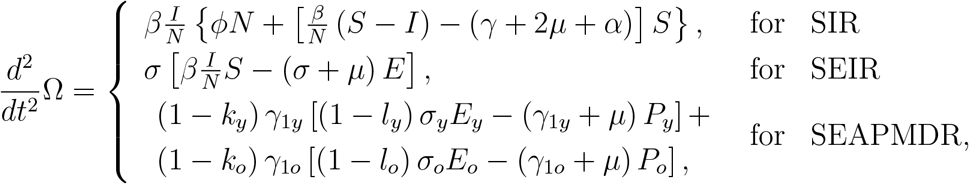which changes the signal from positive to negative at d2Ω/dt2 = 0. Hence, Ω has upward concavity at the beginning of the epidemic and downward concavity at the ending phase of the epidemic. For instance, the number of exposed individuals E in the SEIR model initially increases (dE/dt > 0), attains a maximum value (dE/dt = 0), and decreases since after (dE/dt < 0). Hence, the change in the concavity occurs at the inflection time (point) τ satisfying dE/dt = 0, that is, βIS/N − (σ + µ) E = 0.
Therefore, the accumulated severe CoViD-19 cases Ω follows a sigmoid-shape [12]. From the first derivative of Ω given by equations (5), (3) and (11), we can retrieve the daily severe covid-19 cases Ωd as
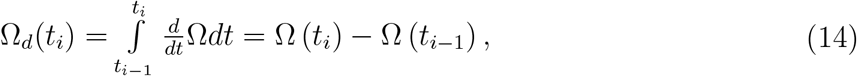where Ωd(0) = 0 at t0 = 0, and Δt = ti − ti−1 = Δt = 1 day, with i = 1, 2, …, and t1 = 1 is the next day in the calendar time, and so on. The inflection time τ occurs at the maximum value of Ωd.
The curve of the effective reproduction number Ref ≈ R0S/N is given by
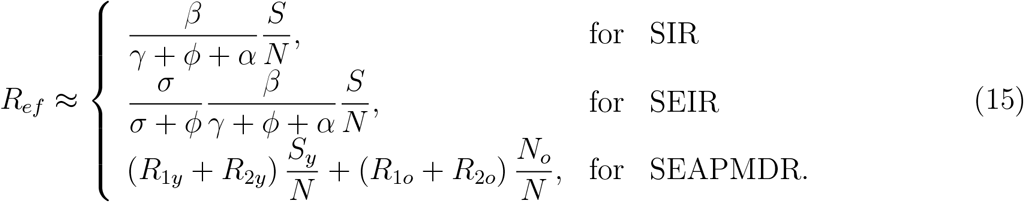
This curve can be used to explain the sigmoid-shape of the accumulated severe CoViD-19 cases Ω.
When d2Ω/dt2 > 0, the upward concavity curve of Ω increases quickly, which is possible if Ref > 1, and one primary case generates more than one secondary case. However, when d2Ω/dt2 < 0, the downward concavity curve of Ω increases slowly reaching an asymptote, which is possible if Ref < 1, and one primary case generates less than one secondary case. Hence, the effective reproduction number Ref decreases monotonically from R0 at t = 0 up to one at the inflection time τ (upward concavity of Ω), and maintains its decreasing trend up to an asymptote (zero, if µ = 0), forming the phase of the downward concavity of the curve Ω. However, Ref = 1 does not occur at the inflection time τ (see below).
3 Results
We estimate the transmission rate β for the SIR, SEIR, and SEAPMDR models presented in the preceding section against the severe CoViD-19 data collection. The basic reproduction number R0 is then calculated for São Paulo State (Brazil) and Spain.
São Paulo State has 44.6 million inhabitants (demographic density, 177/km2) with 15.3% of the population comprised of elder individuals [8]. The first case was registered on February 26, and partial quarantine was implemented on March 24. The sum of the incubation (1/σ) and pre-symptomatic (1/γ1) periods is 9 days, for this reason it is expected a delay of around 9 days since the infection and the CoViD-19 onset. Therefore, we estimate the basic reproduction number considering the collected data from February 26 to April 2.
Spain has 47.4 million inhabitants (demographic density, 92.3/km2) with 25.8% of the population comprised of elder individuals [9]. The first case was registered on January 31, and the lockdown was implemented on March 16. Considering a delay of around 9 days, we estimate the basic reproduction number considering the collected data from January 31 to March 25.
To estimate the parameter β, we calculate
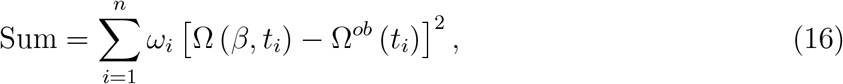where Ω (β, ti) is the accumulated severe CoViD-19 cases calculated from the dynamic system (SIR, SEIR and SEAPMDR models), and Ωob (ti) is the accumulated severe CoViD-19 registered cases at day ti, that is,
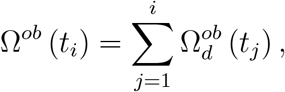where 
is the severe CoViD-19 cases registered at day tj. We consider the same weight for all data, that is, we let ωi = 1. The value of β that minimizes Sum is the fitted value.
Instead of applying the least square estimation method, we calculate the sum of the squared differences between the calculated Ω and the observed data Ωob. The reason behind this simplification relies on the fitting of the model parameter based on a unique observed variable (Ω) of the dynamic system, which is not appropriate [13]. However, this simplified method of parameter evaluation does not provide uncertainties associated with the parameters. The effects of these uncertainties on the epidemic can be assessed by the global sensitivity analysis [14].
Once the transmission rate β is estimated, we calculate R0 using equations (A.7), (A.3) and (B.8) for, respectively, SIR, SEIR and SEAPMDR models. Notice that these three expressions for R0 give secondary cases produced by one primary case introduced in a completely susceptible population. Notice that the fatality rate α affects R0 in the SIR and SEIR models, but not in the SEAPMDR model. The reason behind it is the severe CoViD-19 cases transmitting in the SIR and SEIR models but not in the SEAPMDR model. Hence, in the latter model, one of the sources of uncertainties is removed.
3.1 The SIR model
To estimate the transmission rate, we use equation (16) and Ω given by equation (5). The model parameters are γ = 1/10, α = 0.002 and, for São Paulo State, ϕ = µ = 1/(78.4 × 365) and, for Spain, ϕ = µ = 1/(83.4 × 365) (all in days−1). The value γ = 1/10 days−1 in somehow is an average value among γ, γ1, γ2, and γ3 in the SEAPMDR model (see Table 1). The transmission rate β is estimated, and the basic reproduction number R0 is calculated using equation (A.7). We estimate the basic reproduction number using equation (4) with different infective individuals at t = 0.
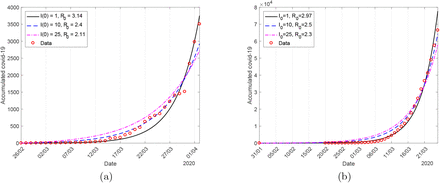
For the data collected from São Paulo State, we obtained for I(0) = 1, R0 = 3.14 with Sum = 8.02 × 105, for I(0) = 10, R0 = 2.4 with Sum = 8.49 × 105, for I(0) = 25, R0 = 2.11 with Sum = 1.86 × 106, and for I(0) = 100, R0 = 1.62 with Sum = 5.87 × 106. Other initial conditions are S(0) = 44.6 million and R(0) = 0. The lowest Sum occurs when R0 = 3.14.
For the data collected from Spain, we obtained for I(0) = 1, R0 = 2.97 with Sum = 4.16 × 108, for I(0) = 10, R0 = 2.5 with Sum = 6.32 × 108, for I(0) = 25, R0 = 2.3 with Sum = 1.13 × 109, and for I(0) = 100, R0 = 2.06 with Sum = 1.19 × 109. Other initial conditions are S(0) = 47.4 million and R(0) = 0. The lowest Sum occurs when R0 = 2.97.
Figure 1 shows the estimated curve Ω for São Paulo (a) and Spain (b) with three different initial conditions (I(0) = 1, 10, and 25).
The estimated curve Ω for São Paulo (a) and Spain (b) with three different initial conditions I(0) = 1 (continuous curve), 10 (dashed curve), and 25 (dashed and dotted curve).
We observe that the larger the value of I(0), the small is the estimated R0. For instance, R0 with I(0) = 100 for São Paulo State is about half that with I(0) = 1. By the stringent definition of R0, we must consider I(0) = 1. However, the initial condition I(0) > 1 mimics the first case of CoViD-19 occurring earlier than the time t = 0. The Singapore University of Technology and Design [15] estimated R0 using I(0) = 100 for different countries, underestimating the basic reproduction number.
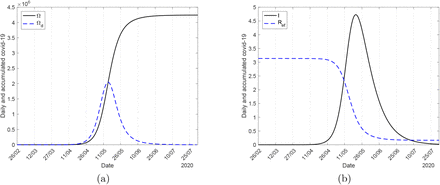
Let us illustrate the curves Ω, Ωd, I and Ref for the SIR model in the natural (occurring without any control) epidemic. Equations (5), (14) and (15) are used to obtain Ω, Ωd and Ref, and I is the solution of the system of equations (4). The inflection time calculated from 
is τ = 78 (calendar time May 14). Figure 2 shows the estimated curve of Ω and the daily curve Ωd (a), and the epidemic curve I and effective reproduction number Ref (b). In Figure 2(a), Ω was divided by 10 to fit in the same frame with Ωd, and in 2(b), I was divided by 3 × 106 to fit in the same frame with Ref. We used data collected from São Paulo State, and the initial conditions are S(0) = 44.6 million, I(0) = 1, and R(0) = 0, yielding R0 = 3.14.
The estimated curve of Ω and the daily curve Ωd (a), and the epidemic curve I and effective reproduction number Ref (b).
The maximum value of Ωd occurs at t = 78 (calendar time May 14), equal to the calculated inflection time τ. The maximum value of I occurs at t = 84 (calendar time May 20), equal to when Ref = 1.
When α > 0, the steady-state fraction of the susceptible individuals s∗ is given by equation (A.10), and the effective reproduction number Ref given by equation (15) is an approximated value. However, when α = 0, s∗ is given by equation (A.12), and Ref = R0S/N, with R0 = β/γ + ϕ + α. Using the same model parameters values and initial conditions in Figure 2, the maximum values for Ωd and I occurred at, respectively, t = 77 and 84, the inflection time is τ = 77, and Ref = 1 occurred at t = 84. For α = 0, we have R0 = 3.20, which is 2% higher than R0 = 3.14. Therefore, Ref = 1 occurs at the maximum value (peak) of the epidemic curve I.
3.2 The SEIR model
To estimate the transmission rate, we use equation (16) and Ω given by equation (3). The model parameters are those used in the SIR model: γ = 1/10, α = 0.002, and, for São Paulo State, ϕ = µ = 1/(78.4×365) and, for Spain, ϕ = µ = 1/(83.4×365) (all in days−1). For the additional parameter, we let σ = 1/5 days−1 (see Table 1). The transmission rate β is estimated, and the basic reproduction number R0 is calculated using equation (A.7). We estimate the basic reproduction number using equation (1) with the initial conditions S(0) = N0, E(0) = 0, R(0) = 0, and varying I(0).
For the data collected from São Paulo State, with S(0) = 44.6 million, we obtained for I(0) = 1, R0 = 7.25 with Sum = 1.36 × 106, for I(0) = 10, R0 = 4.7 with Sum = 4.52 × 105, for I(0) = 25, R0 = 3.82 with Sum = 1 × 106, and for I(0) = 100, R0 = 2.6 with Sum = 3.68 × 106. The lowest Sum occurs when R0 = 4.7.
For the data collected from Spain, with S(0) = 47.4 million, we obtained for I(0) = 1, R0 = 6.27 with Sum = 2.39×108, for I(0) = 10, R0 = 4.75 with Sum = 7.64×107, for I(0) = 25, R0 = 4.21 with Sum = 2.21 × 108, and for I(0) = 100, R0 = 3.38 with Sum = 7.57 × 108. The lowest Sum occurs when R0 = 4.75.
Figure 3 shows the estimated curve Ω for São Paulo (a) and Spain (b) with three different initial conditions (I(0) = 1, 10, and 25).
The estimated curve Ω for São Paulo (a) and Spain (b) with three different initial conditions I(0) = 1 (continuous curve), 10 (dashed curve), and 25 (dashed and dotted curve).
Notice that σ/ (σ + µ) = 0.99999, hence, R0 given by equations (A.7) and (A.3) must be equal if β is the same for the SIR and SEIR models. However, β is estimated by the dynamic systems (4) or (1) against the accumulated severe CoViD-19 cases. For this reason, the estimated β must be different in the SIR and SEIR models.
Comparing with the estimated R0 provided by the SIR model, we observe that the SEIR model estimated with a higher value. Let us assess the role played by the incubation period σ−1 in the SEIR model considering the initial conditions S(0) = N0, E(0) = 0, I(0) = 1, and R(0) = 0. For σ−1 = 10 days, R0 = 11.27 with Sum = 1.15 × 106, for σ−1 = 1 day, R0 = 3.92 with Sum = 8.92 × 105, for σ−1 = 10−1 days (2.4 hours), R0 = 3.2 with Sum = 8.06 × 105, and for σ−1 = 10−3 days (1.44 minutes), R0 = 3.14 with Sum = 7.96 × 105. As σ−1 decreases (σ increases), R0 approaches (when σ → ∞) to that estimated by the SIR model (R0 = 3.14). By disregarding the incubation period, the SIR model provides a relatively lower estimation for R0 in comparison with the SEIR model. To overcome this period and fit the same set of the severe CoViD-19 cases, the transmission rate of SARS-CoV-2 must be much higher in the SEIR than in the SIR model. Therefore, the inclusion of the exposed individuals delays the onset of disease (or the entering into an infectious compartment), and the virus must infect more individuals (increased R0).
3.3 The SEAPMDR model
To estimate the transmission rates, we consider βy = β1y = β2y = β3y and βo = β1o = β2o = β3o = ψβy, and we use equation (16) and Ω given by equation (11). The values for the model parameters are those given in Table 1. The basic reproduction number R0 is calculated using equation (12).
The initial conditions supplied to the system of equations (7), (8) and (9) are, for young and elder subpopulations,
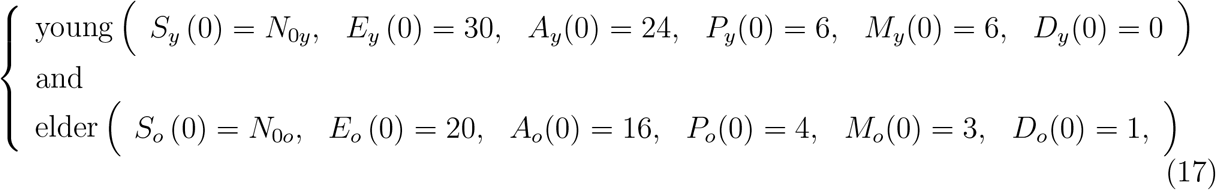plus R(0) = 0, where the initial simulation time t = 0 corresponds to the calendar time when the first case was confirmed (February 26 for São Paulo State, and January 31 for Spain). For São Paulo State, N0y = 37.8 million and N0o = 6.8 million, and for Spain, N0y = 35.17 million and N0o = 12.23 million. (See [16] for details in the initial conditions’ setup.)
For the data collected from São Paulo State, we obtained R0 = 6.54, with Sum = 7.75 × 105, while for the data collected from Spain, we obtained R0 = 5.88, with Sum = 1.1 × 108. Figure 4 shows the estimated curve Ω for São Paulo State (a) and Spain (b).
The estimated curve Ω and the observed accumulated cases for São Paulo State (a) and Spain (b).
Suppose we let zy = zo = 0 (mild CoViD-19 cases do not transmit) and χy = χo = 1 (asymptomatic individuals do not relapse to mild CoViD-19). In that case, the estimated basic reproduction number is R0 = 6.26 for São Paulo State, with Sum = 7.56 × 105, and R0 = 5.67 for Spain, with Sum = 1.18 × 108.
For the SEIR model, let us consider as the initial conditions E(0) = 50 (sum of Ey (0) + Eo (0)), I(0) = 1 and R(0) = 0, and S(0) = 44.6 million for São Paulo State and S(0) = 47.4 million for Spain. The estimated basic reproduction number for São Paulo State is R0 = 3.53 with Sum = 1.56 × 106 and for Spain, R0 = 4.07 with Sum = 2.53 × 108.
4 Discussion
There are different manners to define an epidemic curve. For instance, one possible definition is the curve formed by those positive for serological and PCR tests. However, in the early phase of the epidemic, the CoViD-19 epidemic curve must be defined by severe cases, which are the only available data. In the SEAPMDR model, the CoViD-19 epidemic curve was retrieved by estimating the transmission rates of asymptomatic, pre-diseased, and a fraction of mild classes. In [11], it was shown that the ratio between non-apparent (sum of compartments E, A, and P) and apparent (sum of compartments M and D) CoViD-19 is around 24, showing that SARS-CoV-2 is being transmitted by a huge number of hidden cases.
In the SEAPMDR model, the initial conditions E(0) = 50 and I(0) = 1 were supplied to the dynamic system, resulting in R0 = 6.54 (São Paulo State) and R0 = 5.88 (Spain), higher than estimations usually accepted. Instead of comparing the SIR model, let us compare the SEIR model with the same initial conditions supplied to the SEAPMDR model. The estimated basic reproduction number for São Paulo State was R0 = 3.92, and for Spain, R0 = 4.41.
Comparing SIR, SEIR, and SEAPMDR models, as the model incorporates more aspects of the natural history of the infection [17], higher becomes the estimation of R0. There is no other alternative for the SIR and SEIR models except considering severe CoViD-19 cases as infective. However, in the SEAPMDR model, the asymptomatic (A), pre-diseased (P), and a fraction of mild CoViD-19 (M) individuals are transmitting SARS-CoV-2, but the severe CoViD-19 (D) individuals are isolated and do not contribute, except to infect the hospital staff [11].
As we have pointed out, at the beginning and also in the early phase of the CoViD-19 epidemic, only hospitalized severe CoViD-19 cases were registered after the confirmation by serological and or PCR tests. These individuals are isolated in hospitals (receiving treatment) or discharged from hospitals but recommend being isolated in their homes. Then, somehow the majority of these individuals are not participating in the populational SARS-CoV-2 chain transmission.
In the SEAPMDR model, there are several infectious classes, but the severe CoViD-19 cases do not transmit the SARS-CoV-2, for this reason, R0 does not depend on the additional mortality rates αy and αo (see equations (12) and (13)). On the other hand, in the SIR and SEIR models, there is only one infectious class, and R0 depends on the additional mortality rate α (see equations (A.7) and (A.3)). Notice that in the SIR and SEIR models, the unique way to estimate the transmission rate is that severe covid-9 cases form the infective class I.
Besides the consideration of the CoViD-19 data, we discuss the magnitude of R0. Both SIR and SEIR models provided lower estimates for R0 than the SEAPMDR model.
As we have pointed out, Li et al. [3] estimated Ref = 2.38 using the range of data recorded from 54 days after the epidemic’s onset to 16 days after the lockdown. From Figure 2b corresponding to the SIR model with R0 = 3.14 (simulation time t = 0), we observe that Ref R0 up to the simulation time t = 50 initiates a quick decreasing phase at t = 60. However, for the SEAPMDR model without interventions, R0 = 6.54 decreases to Ref = 5.41 at simulation time t = 50. However, the partial quarantine was introduced on March 24 (t = 27), and 16 days later on April 9 (t = 45), we have Ref = 2.92 considering protective measures in the SEAPMDR model (see [16]). This value is close to that estimated by Li et al., remembering that they did not take the initial time of estimation when the first case of CoViD-19 occurred.
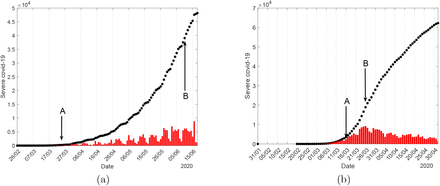
The curve of accumulated CoViD-19 cases Ω obtained from equation (11) shown in Figure 2 has a sigmoid-shape. This curve presents a quick increase during the first phase (Ref > 1, with upward concavity) followed by a slow increase (Ref < 1, with downward concavity), where Ref is given by equation (15). Figure 2 showed Ω and Ref corresponding to the natural epidemic. In Figure 5, we show the daily Ωd and the accumulated severe CoViD-19 cases Ωob collected from São Paulo State (a) and Spain (b), where A indicates the time at which quarantine was introduced, and B represents the inflection time. To be fitted together in the same frame, the accumulated data set was divided by 4. The observed severe CoViD-19 data carry on the effects of the quarantine and the protective measures (face mask, washing hands with alcohol and gel, social distancing, etc.) adopted by individuals that reduced the transmission of SARS-CoV-2. In São Paulo State, a partial quarantine was introduced on March 24 isolating approximately 53% of the population [8], and a rigid lockdown in Spain was introduced on March 16 isolating perhaps 90% or more.
The daily (bars) and the accumulated (points) severe covid-19 cases in São Paulo State (a) and Spain (b), where A indicates the time at which quarantine was introduced, and B indicates the inflection time.
Let us define the threshold of the proportion in isolation in a population as qth = 1 − 1/R0. If the proportion in quarantine q is higher than qth, we must have Ref < 1, and the observed accumulated CoViD-19 cases must present downward concavity and upward concavity if q < qth. For São Paulo State, we have q = 0.53. At Ref = 1, we have the inflection time (change from upward to downward concavity). Using the value of R0 estimated in the preceding section, for the SIR model (R0 estimated with I(0) = 1) we have qth = 0.68 for São Paulo State, and qth = 0.66 for Spain. For the SEAPMDR model, we have qth = 0.85 for São Paulo State, and qth = 0.83 for Spain. The SEAPMDR model shows that isolating 85% in the population or more controls the epidemic, but the SIR model predicts less proportion of isolation, 68% or more.
As shown in Figure 5, the inflection time occurred approximately on June 10 in São Paulo State and on March 26 in Spain. The elapsed time between the implementation of quarantine (A) and the inflection time (B) is 78 days in São Paulo State and 10 days in Spain. From Figure 2, for São Paulo State using the SIR model, the period from the beginning of the epidemic until the inflection time was 78 days. This period, which was calculated for the natural epidemic, must be lesser when considering the epidemic under isolation and protective measures. Hence, the actual R0 must be higher than 3.14. However, if we consider R0 = 2.11 estimated from the SIR model using I(0) = 25, we obtain qth = 0.53 for São Paulo State resulting in q = qth. In other words, the inflection time must occur 9 days later, when we have Ref = 1 (the effects of any intervention appear 9 days later). As a consequence, the observed accumulated severe CoViD-19 cases must be quite similar to that observed in Spain. Notice that the inflection time occurred 10 days after the implementation of lockdown in Spain. The long time to reach the inflection time in São Paulo State (78 days) may indicate that the SIR model underestimated R0, and that estimated by the SEAPMDR model seems to be more reliable.
Finally, the SEAPMDR model proposed by Yang et al. [6] at the beginning of the CoViD-19 epidemic deserves some considerations. At the beginning of the epidemic, the severe acute respiratory syndrome cases were hospitalized and confirmed as CoViD-19 after some tests (many patients died and were diagnosed post mortem as CoViD-19 by a test). This disease’s rapid spread indicated that possibly asymptomatic and mild CoViD-19 cases transmitted SARS-CoV-2 once severe CoViD-19 patients were isolated in hospitals. Additionally, the model considered pre-symptomatic individuals transmitting infection, which was confirmed later. Besides these aspects, the model considered the increased fatality among elder individuals. Minimalist incorporation of this disease’s severity in the model divided the population into two groups: young (under 60 years old) and elder (above 60 years old) individuals. (Notably, the consideration of two subpopulations by the SEAPMDR model predicted three times lower number of deaths than that indicated in [2].) To estimate the basic reproduction number, the authors restricted data collection during the period without any control.
5 Conclusion
This work’s goal was to demonstrate that the early applied SIR and SEIR models underestimated R0 misusing the severe CoVid-19 data collection. For this reason, we formulated the SEAPMDR model incorporating essential aspects related to the natural history of the infection. For instance, the incorporation of the asymptomatic and pre-diseased individuals, mild CoViD-19 cases, and different fatality rates depending on age must improve the mathematical model to describe the CoViD-19 epidemic. Additionally, these more elaborated models could consider the severe CoViD-19 cases being isolated, and SARS-CoV-2 is transmitted by asymptomatic and pre-diseased individuals, for instance. Hence, the SEAPMDR must provide a more accurate estimation of R0. Specifically, when the severe CoViD-19 cases may not transmit SARS-CoV-2 populationally, the SIR and SEIR models structured in only one infectious compartment are not suitable to estimate the basic reproduction number R0. It is worth stressing that the reliable estimation of R0 must consider the time range from the first case to the last case before the first case affected by interventions.
Data Availability
Data obtained from ministery of health fo Spain and São Paulo State.
https://www.seade.gov.br/coronavirus/
https://www.mscbs.gob.es/profesionales/saludPublica/ccayes/alertasActual/nCov/home.htm
Funding
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Conflicts of interest/Competing interests
Not applicable.
Availability of data and material
The data that support the findings of this study are openly available in SP contra o novo coronavírus (Boletim completo) at https://www.seade.gov.br/coronavirus/, and Spain Covid19 at https://cnecovid.isciii.es/covid19/.
Author contributions
Hyun Mo Yang: Conceptualization, Methodology, Formal analysis, Writing - Original draft preparation, Validation, Supervision. Luis Pedro Lombardi Junior: Software, Data Curation, Visualization, Validation. Ariana Campos Yang: Conceptualization, Validation, Investigation.
A The steady-state analysis of the SIR and SEIR models
We present the analysis of the SIR and SEIR models.
A.1 The SEIR model
The system of equations (1) does not reach a steady-state, except if ϕ = µ + αI/N. However, the system (1) in terms of the fractions attains steady-state. Defining the fraction x = X/N, with X = {S, E, I, R}, we have
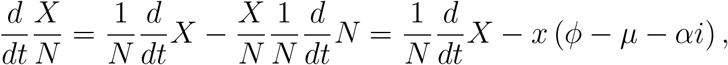using equation (2), and the system of equations (1) becomes
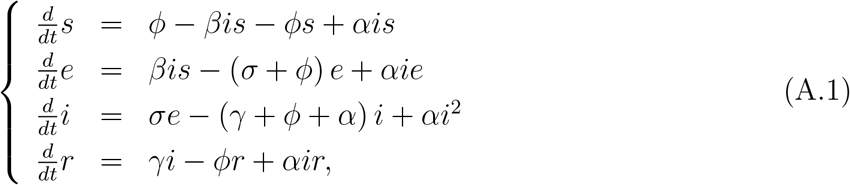with s + e + i + r = 1, hence, the equation for r can be decoupled from the system, through r = 1 − e − s − i. Notice that d (s + e + i + r) /dt = 0, and the system of equations in terms of fractions attain a steady state.
The system of equations (A.1), dropping out the decoupled equation for r, has two equilibrium points: The trivial (disease-free) equilibrium point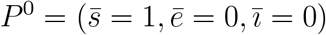 
and non-trivial (epidemic) equilibrium point 
.
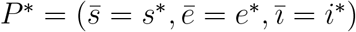Let us assess the stability of P 0 by applying the next generation matrix theory considering the vector of variables x = (e, i) [18]. The next generation matrix is constructed considering a subsystem of equation (9) taking into account the state-at-infection (e) and the states-of-infectiousness (i) [18], resulting in x = (e, i). In a matrix form, the subsystem is written as
where the vectors f and v are defined below, with the partial derivatives of f and v evaluated at P0 being given by
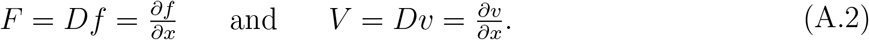
Depending on the choice of vectors f and v, we can obtain the reduced reproduction number or the fraction of susceptible persons at endemic level [19].
To obtain the basic reproduction number R0, diagonal matrix V is considered. Hence, the vectors f and v are
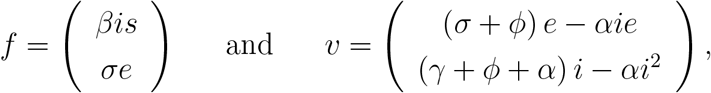resulting in F and V given by
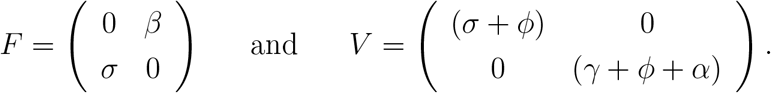
The characteristic equation corresponding to FV −1 is
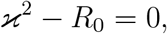and the spectral radius 
, where the basic reproduction number R0 is
Instead of the spectral radius 
, we applied the procedure in [19] (the sum of coefficients of the characteristic equation) and proved in [20], resulting in the threshold R0. Hence, the trivial equilibrium point P 0 is locally asymptotically stable (LAS) if R0 < 1.
To obtain the fraction of susceptible individuals at endemic equilibrium s∗, F must be the most straightforward (matrix with the least number of non-zero elements). Hence, the vectors f and v are
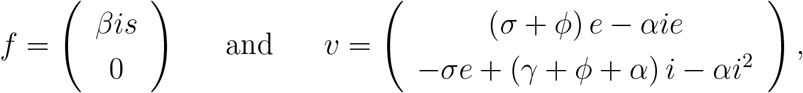resulting in F and V given by
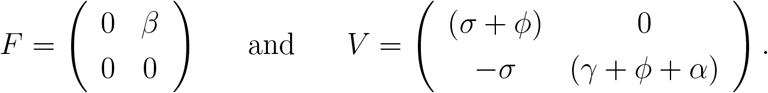
The characteristic equation corresponding to FV −1 is
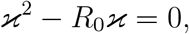and the spectral radius ρ (FV −1) = R0, which is equal to the sum of the coefficients.
Both procedures resulted in the same threshold, hence, according to [21], the inverse of the reduced reproduction number R0 given by equation (A.3) is a function of the fraction of susceptible individuals at endemic equilibrium s∗ through
Hence, we can define the effective reproduction number Ref as
which depends on time, with Ref = R0 at t = 0 (s = 1), and when attains steady-state (Ref = 1), we have s∗ = 1/R0. Notice that Ref = R0s when α = 0 (see below for the SIR
model),
A.2 The SIR model
The SIR model is obtained letting σ → ∞ in the SEIR model, and the system of equations (4) becomes
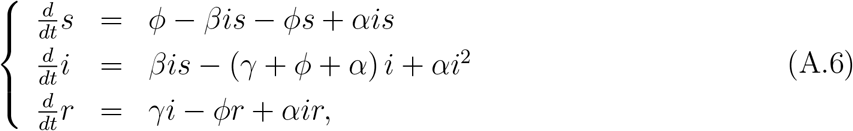with s + i + r = 1, hence, the equation for r can be decoupled from the system, through r = 1 − s − i. The system of equations (A.6), dropping out the decoupled equation for r, has two equilibrium points: The trivial (disease-free) equilibrium point 
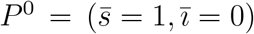and non-trivial (epidemic) equilibrium point 
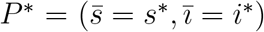. The stability analysis of trivial equilibrium is given from the preceding section letting σ → ∞, and the the basic reproduction number R0 is
The coordinates of the non-trivial equilibrium point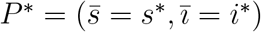 
in the SIR model can be calculated by
where i∗ is the positive root but small than one of the second degree polynomial P2(i) given by
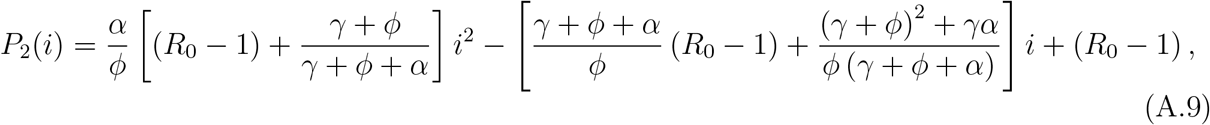which has the value, at i = 1,
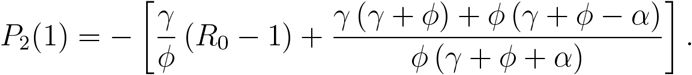When R0 > 1, we have P2(1) < 0 (the condition γ + ϕ > α is satisfied because γ > α), and the two positive roots of P2(i) are such that 
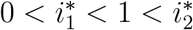. Hence the small root 
is biologically feasible. When R0 = 1, we have 
and 
, hence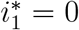 
is biologically feasible. When R0 < 1, we have 
and 
, hence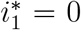 
is biologically feasible. Therefore, the small root 
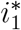, which is biologically feasible, assumes a negative value for R0 < 1, zero at R0 = 1, and a positive value but lower than 1 for R0 > 1. The small root of P2(i) is given by
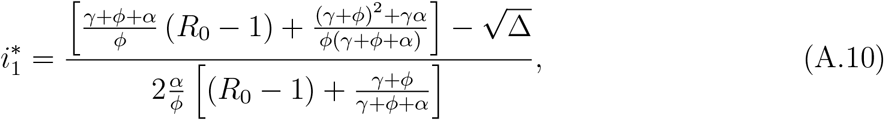where Δ is
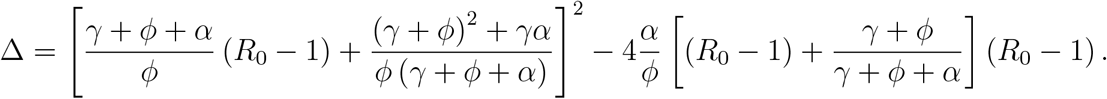
The complexity arises due to the non-constant population under the additional mortality rate. Let us consider α = 0. In this case, P2(i) has a unique positive solution
and the fraction of susceptible individuals, from equation (A.8), is
In this particular case, we have Re = R0s. Hence, for α > 0, comparing equations (A.8) and (A.10), we notice that s∗ has a complex dependency with R0, not simply 1/R0.
Let us assess the stability of the system of equations (A.6) linearized around the trivial equilibrium point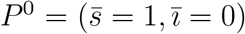 
. The Jacobian matrix J evaluated at the trivial equilibrium point P 0 is
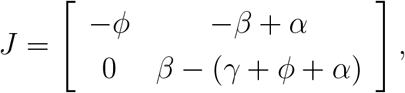with the eigenvalues ρ1 = −ϕ and ρ2 = (γ + ϕ + α) (R0 − 1), where the basic reproduction number R0 is given by (A.7). Hence, P 0 is locally asymptotically stable if R0 < 1. Hence, the linearized system around P 0 has a trajectory for i given by
where A and B are arbitrary values determined by the initial conditions.
When R0 > 1, an introduction of one infectious individual disestablishes the trivial equilibrium point P 0, and the unique positive eigenvalue gives the leaving trajectory. Hence, the escaping trajectory follows 
in the vicinity of P 0 towards the non-trivial equilibrium point P∗. Maidana and Yang [22] provided an example of trajectories (travelling waves) linking P 0 towards P∗ considering a spatial model for the dengue transmission.
To establish a relationship with the linearized system of equations in terms of the fractions, the system of equations (4), using R = N − I − S, is rewritten as
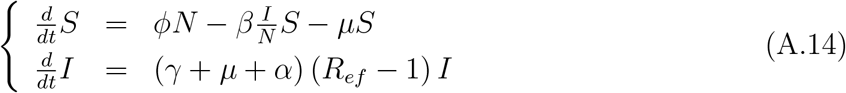where the effective reproduction number Ref is defined by
with the basic reproduction number R0 being given by equation (A.7) changing ϕ by µ, that is, R0 = β/ (γ + µ + α).
Let us analyze the system of equations (A.14) at two boundaries. Let us assume that the first case of CoViD-19 is introduced at t = 0, that is, the initial conditions supplied to equation (A.14) are S(0) = N − 1 and I(0) = 1. For a large population, we can approximate S ∼ N, and the system of equations can be approximated by
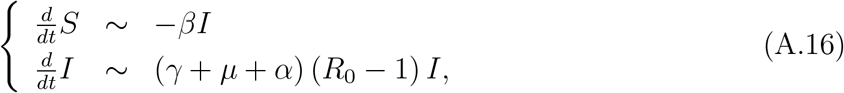with R = N − S − I, and at the beginning of the epidemic, if we estimate the transmission rate β, we can calculate R0 using the expression obtained from the steady-state analysis. The system of equations (A.14) does not approach to a steady-state, but attains it when α = 0. In this case, asymptotically (t → ∞), we have dI/dt = 0 if Ref = R0S/N = 1, that is, S → S∗ = s∗N and I → I∗ = i∗N, where i∗ and s∗ are given by equations (A.11) and (A.12), respectively. Hence, when α = 0, at t = 0, Ref = R0, and when t → ∞ (steady-state), Ref = 1 (see equation (A.12)), from which we retrieve the well known relationship s∗ = 1/R0 [4].
Therefore, based on Ref given by equation (A.15) when ϕ = µ and α = 0, the basic reproduction number R0 obtained from mathematical modelings provides two useful information: At the beginning of the epidemic (t = 0), R0 gives the magnitude of the initial takeoff of the epidemic, and when epidemic reaches the steady-state (after many waves of the epidemic, that is, t → ∞), R0 measures its severity providing the fraction of susceptible individuals, that is, s∗ = 1/R0. Between these two extremes, the effective reproduction number Ref dictates the course of an epidemic, which follows decaying oscillations around Ref = 1 [7]. It is worth stressing that Ref given by equation (A.15) is valid only when ϕ = µ and α = 0, and when one of these conditions is not valid, Ref given by equation (A.15) can be used as an approximated value.
From equation (A.16), the solution for I is 
, which is equal to equation (A.13) when A = 0 and B = 1.
B The steady-state analysis of the SEAPMDR model
The system of equations (7), (8) and (9) does not reach steady state, except if ϕ = µ + (αyDy + αoDo) /N, when the total size of the population is constant. However, the system of equations (7), (8) and (9) in term of fractions attains steady-state. Defining the fraction xj = Xj/N, for j = y, o, with Xj = {Sj, Ej, Aj, Pj, Mj, Dj, R}, we have
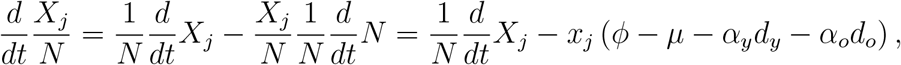using equation (10), and the system of equations (7), (8) and (9) in terms of fractions become, for susceptible individuals,
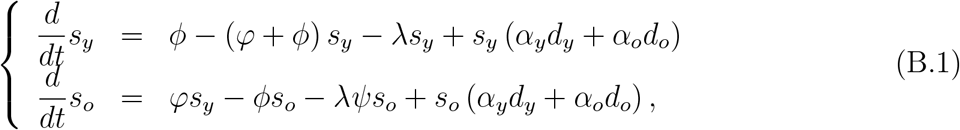for infected individuals,
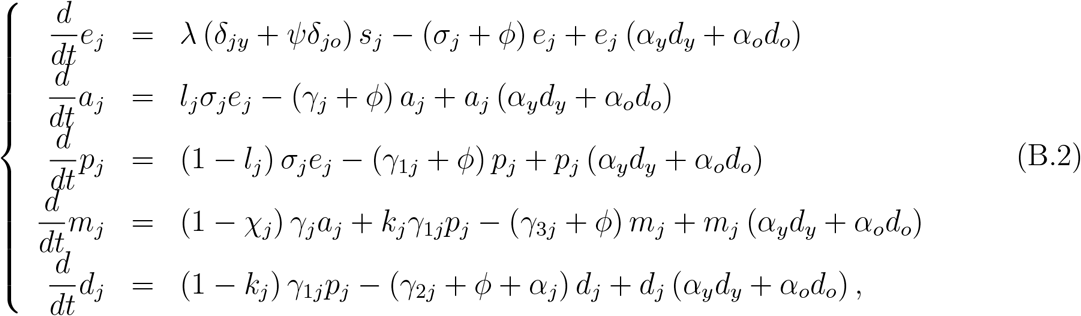and for recovered individuals,
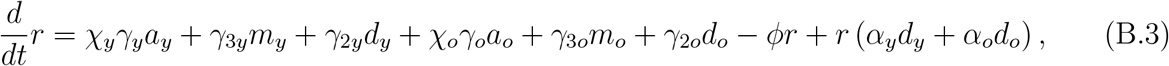where λ is the force of infection given by equation (6) re-written as
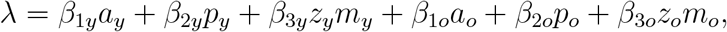and
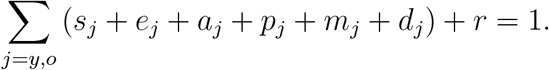
This new system of equations has a steady-state, that is, the number of individuals in all classes varies with time. However, their fractions attain a steady-state (the sum of derivatives of all classes is zero).
The trivial (disease-free) equilibrium point P 0 of the new system of equations (B.1), (B.2) and (B.3) is given by
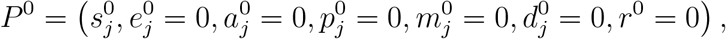for j = y and o, where
with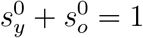 
.
Let us assess the stability of P 0 by applying the next generation matrix theory considering the vector of variables x = (ey, ay, py, my, eo, ao, po, mo) [18]. We apply method proposed in [19] and proved in [20]. To obtain the basic reproduction number, diagonal matrix V is considered. Hence, the vectors f and v are
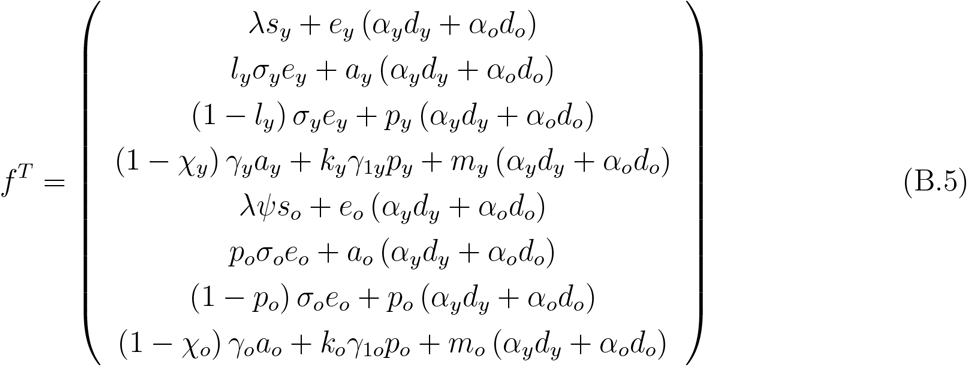and
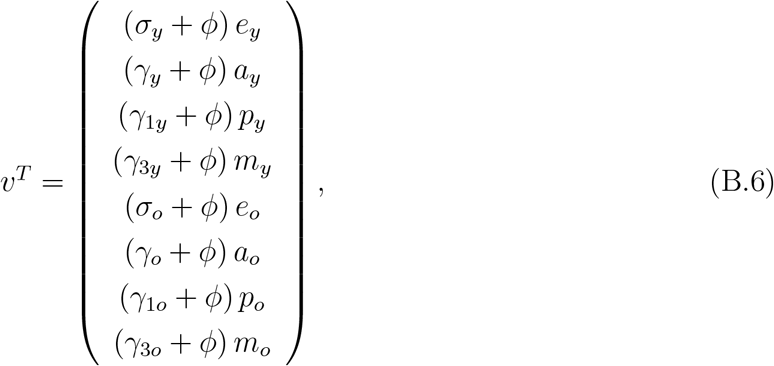where the superscript T stands for the transposition of a matrix, from which we obtain the matrices F and V (see [18]) evaluated at the trivial equilibrium P 0, which were omitted. The next generation matrix FV −1 is
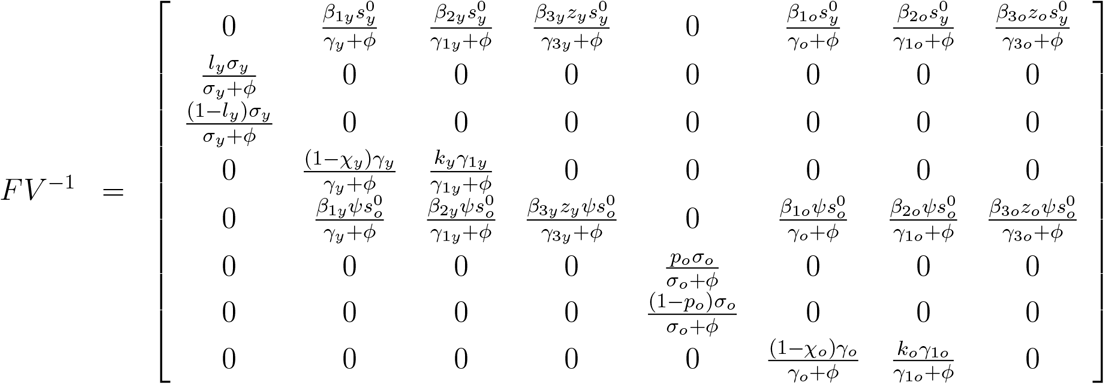and the characteristic equation corresponding to FV −1 is
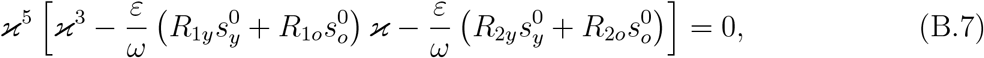with the basic reproduction number R0 being given by
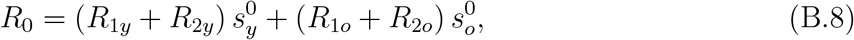where the initial fractions 
and 
are given by equation (B.4), and the partial basic reproduction numbers R1y, R2y, R1o, and R2o are given by equation (13) in the main text. The spectral radius ρ (FV −1) is the biggest solution of a third-degree polynomial, not easy to evaluate. The procedure proposed in [19] allows us to obtain the threshold R0 as the sum of coefficients of the characteristic equation, where R0 is the basic reproduction number given by equation (12) in the main text. Hence, the trivial equilibrium point P 0 is locally asymptotically stable if R0 < 1.
Footnotes
emails: hyunyang{at}ime.unicamp.br, luispedro_jr{at}hotmail.com, arianacy{at}gmail.com
References
