Optimizing ventilation cycles to control airborne transmission risk of SARS-CoV2 in school classrooms

2.1 GN-model with perfect mixing and face masks

The infection risk model used in the present analysis is essentially based on the Gammaitoni-Nucci (GN) model, which is adequate for confined, ventilated environments [Gammaitoni 1997]. This model is based on the assumption that newly-produced viral particles are instantly diluted over the whole environment volume (perfect-mixing) and that the emission rate parameter ER_q (emission rate, i.e. number of viral particles generated per hour by each infective subject) is known, at least as an averaged value over the exposure time 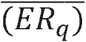A correct estimation for the emission rate parameter ER_q is not trivial and mostly based on a semi-empirical approach combining viral load measurements from clinical trials and reverse engineering from observed outbreaks, assuming for ER_q averaged values selected from the variability ranges which arise from the following formula [Morawska 2009]. The “infective viral reduction rate” (IVRR) is the second parameter which enters the GN model and takes into account air ventilation (AER) and gravitational re-deposition (λ): IVRR=AER+λ. A λ value equal 0.5 vol/h was considered during the whole exposure time, on the basis of the half-life in air of the SARS-CoV-2 virus of about 1h as reported in [van Doremalen 2020]. According to the GN model, the risk of infection in a volume V, where one infective subject is present and the initial number of viral particles is n₀ (which can be different from zero) is then given by the general formula:

Where

To account for the effect of PPE (personal protective equipment, in this case, face masks) in reducing both the number of viral particles generated by infective subjects, and also reducing the likelihood of inhalation of viral particles by exposed subjects, Eq (1)is extended introducing two scaling factors:

(1- f_out), which represents the fractional reduction of the generated viral load, and

(1- f_in), which represents the fractional reduction of inhaled viral load, under the assumption that all subjects are wearing a mask. Eq. (1) can then be rewritten as:

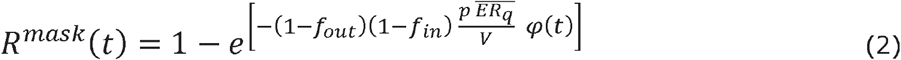
If masks are not being worn, f_in and f_out are both zero.

2.2 Influence of windows opening function on the infective virus removal rate (IVRR)

Windows opening implies a periodic activation of air exchanges per hour, which are supposed to occur only during lesson breaks. Therefore, the IVRR function in (3) become a periodic rectangular wave function over the full lesson time, with peaks influenced by higher values of the air exchange rate (AER) as due to complete windows opening (2vol/h) or mechanical ventilation (up to 10 vol/h). In this study we explore the influence on the classroom risk function of different cycles (and levels) of the AER within the IRVV function by changing the time duration of lecture and breaks. Fig. 2 report only two exemplary cycles (long and short windows opening cycles) taken as input for the results shown in Fig. 3-4, whereas optimization of the risk function shown in Fig. 5-6 considered 3500 different combination of t_brk and t_lec with a time resolution of 1 min which generated the same amount of different ventilation cycles. Another factor to be considered is the effective volume to be considered to dilute the aerosol viral cloud under the perfect mixing approximation. According to recent CFD simulations of aerosol cloud in classrooms [Abuhegazy 2020], aerosol particles from a student source would not be diluted over the entire volume even after a transient of 300s and the viral cloud volume during the first part of the emission transient would be negligible compared to V. For these reasons an effective lower volume V_eff = 0.85 V in equation (3) and (4) was considered for the present analysis.

In the present work, the GN-model is based on the concept of cumulative risk. In a scenario where the infective source is removed from the environment (e.g. student or teacher leaving the classroom), the ER_q parameter in Eq (1) and (2) would become zero. However, we can observe that even when ER_q =0 in (2), the infection risk 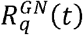would remain greater than zero, because of the multiplicative factor cp φq(t) (and intuitively, due to the viral load already present in the environment).

Another underlying assumption, which is valid at least in Italian secondary schools and in many schools in EU countries, is that the susceptible subjects at the beginning (S₀) remain always the same and do not vary over the course of the school day. For at least one infection to occur, the cumulative risk R_c (t)= C(t)/S₀ must be greater than 1/ S₀. Therefore, the condition for zero infections to occur over the total exposure time is: and not R_lec,i (t) < 1/S₀.

Thus, at the end of a typical school day, one obtains the cumulative risk of infections with one infective source as given by:

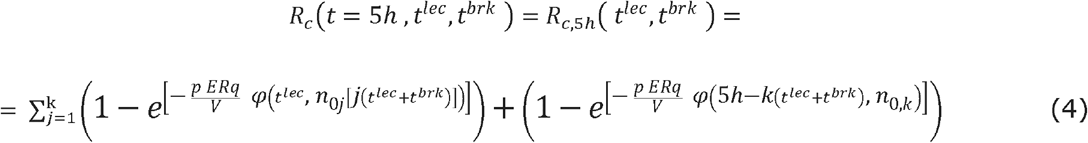
In equation (4), is the integer number of periods (lesson + break) before the last period. One may observe that the last lecture window could be less than t^lec in order not to overcome 5h of total lectures+breaks time. Equation (4) clearly shows that for a given classroom at the end of a school day, the only variables influencing the cumulative risk of airborne contagion (and the total number of infections) are the time duration of lectures (t^lec) and the time duration of breaks (t^brk), since the other model parameters (V, N, IVRR, p, ER_q, f_out, f_in) can be considered either fixed or not controllable for a given classroom and a given local regulation. Two situations were separately considered. First, one positive student source remaining for 5 h in the same classroom but exiting it at each break interval (ER_q =0 at each break). Second, a positive teacher source supposed to remain for 2 hours only with higher ER_q levels. In fact, a high school teacher stays in the same classroom not more than two hours a day on average, moving to a new classroom afterwards. A python routine have been implemented to solve eq. (1-2) and (4) for both cases.

3.1. Optimum ventilation profiles and safety zones

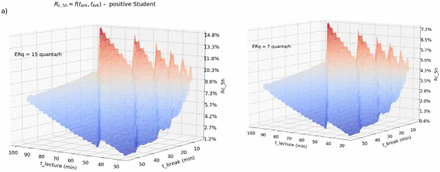
Cumulative risk curves R_c (t) are shown in Fig. 1 and 2 as a function of two variable parameters as shown in Equation (4): t^lec (lecture time, when ventilation is turned off) and t^brk (duration of breaks, when ventilation is active). All surfaces were calculated for a typical classroom of volume 8 * 7 * 3 ≅ 170 m³. For the teacher case, higher levels of ER_q compared to the student case were required to account for a higher (average) speak activity. In all simulations the ER_q values employed were selected from published data [Buonanno 2020] for the case of standing person with normal (ER_q about 25 quanta h^-1) and lowered vocal activity (average ER_q down to 15 quanta h^-1). The latter case refers to a person speaking at moderate volume. This could be the case of a teacher speaking with a microphone connected to a voice amplification system. Even if staying in a classroom less than students (in average for only two hours), an infective teacher speaking most of that time will be a much greater viral source for airborne transmission and the corresponding risk curves will increase more steeply in the first 2h of exposure. After a teacher left the room, the ER_q in that room drops to zero, but the viral charge previously emitted by him/her will still be present for the next hours (although it will lower down after several ventilation cycles).

• Download figure
• Open in new tab

Figure 1

a,b) Cumulative risk function after 5h exposure as a function of lecture and break duration in the case of an infective teacher in classroom, for high (a) and low (b) emission rates. Hypotheses: classroom volume of 170 m3 and worse case for the effective wearing time of surgical masks (fin=0.15, fout=0.45).

• Download figure
• Open in new tab

Figure 2

a,b) as in Fig. 1 but for the case of an infective student source.

As previously stated, a significant risk reduction could be obtained with more frequent ventilation. Thus, there is motivation for finding an optimal set of t^lec,t^brk that would minimize R_c,5h (t^lec,t^brk), noting that only limited actions can be undertaken to vary the other exogenous parameters. Classroom volumes are usually fixed (except for the very few cases in which new spaces have been allocated in the current year). Second, acting on mask filter capabilities is also limited. That is, one may think it would improve the mask parameters f_out and f_in by requesting students to wear ffp2 masks all of the time, but this prescription for students younger than 18 years has been excluded by most regulators. In fact, wearing high-filtering masks in school contexts for long periods may expose students to other respiratory risks. The average pulmonary inflation p cannot be controlled in a lecture context and is reasonably known for human body. Finally, the critical emission rate parameter ER_q depends on actual habits/behaviors and is affected by uncertainties which were taken into account in the present study. In any case, both ER_q and p cannot be controlled by legislation (only ER_q for the teacher case could be lowered down by technical countermeasures, like the adoption of a microphone with amplifier). Instead, acting on ventilation (AER) and then on the directly linked IVVR is feasible in all schools and can be effective, as shown in this and other studies [Buonanno 2021]. On the other hand, maximizing AER in winter would require mechanical ventilation and operating HVAC systems, lacking in most schools. We can act only on windows opening for significant periods of time to increase the air exchange and dilution of the viral load. Therefore, an effective risk reduction pathway is the identification of a numerical optimum for the ventilation schedule as a function of time - AER_opt(t) - which minimizes the cumulative risk within certain boundaries. The risk function to be minimized is z = R_c,5h (t^lec,t^brk) and is represented in Fig. 1 and Fig. 2 and the related contour plots of Fig. 3. As evident, a minimum exists at around (t^lec,t^brk) ≈ (30 min, 50min) since the z function is showing a clear monotonic behavior in the surrounding of the x=y direction. This would imply an unusual recommendation for most schools: class breaks should last longer than the classes themselves. This fact is eventually unsurprising, since opening windows during breaks implies a higher AER-level than during classes (Fig. A1 in Appendix). In addition, this fact is dictated by practical requirements. That is, with low outdoor temperatures (particularly in January–March in schools located in the northern hemisphere) and a concurrent risk for other seasonal diseases, it is only during “lesson breaks” with no students inside the classroom, that one could think to increase the AER substantially by fully opening the windows in a classroom.

• Download figure
• Open in new tab

Figure 3

Contour plots of the cumulative risk function, R_c,5h (t^lec,t^brk) a) Positive student and b) positive teacher case. Continuous lines indicate “thresholds for a new infection” (C = 1) for different classroom groups. The regions they define are called “safety zones” for that group size. Green regions suggest values for t^lec,t^brk which would be safe for the infective teacher as well for the infective student case, i.e. regardless of source type. Hypotheses are the same of Fig. 5.

However, since overly long breaks may also cause practical and organizational difficulties for schools, wider “safety zones” for the variation of t^lec, t^brk are recommended in Fig. 6. These zones are defined below so-called “one-infection thresholds” (varying for different values of the number S0 of students per classroom). A certain combination of t^lec,t^brk from the safety zone would thus provide sufficient ventilation and dilution of the viral load to lower the risk for new indirect infections below 1/S0. That is, no infections would be expected in a group of S0 susceptible individuals if the room were ventilated for an equal period of time 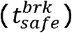at every class break. Green regions suggest values for t^lec, t^brk which would be safe for the infective teacher as well for the infective student case, i.e. regardless of source type. In order to achieve complete safety in a classroom of 30 students exposed for 5 hours, classes should last approximately 45 min but breaks should be very long (about 35 minutes). This would eventually turn into a complex or even unfeasible scheduling challenge for schools (only 3.75 lesson+break cycles would be possible within 5 hours). On the other hand, in a classroom of 15 students only, lessons could last 45-47 min and breaks easily reduced to 15 minutes, allowing 5 entire cycles.