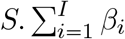The source of individual heterogeneity shapes infectious disease outbreaks

Baptiste Elie, Christian Selinger, Samuel Alizon
doi: https://doi.org/10.1101/2021.02.18.21251983

Abstract

There is known heterogeneity between individuals in infectious disease transmission patterns. The source of this heterogeneity is thought to affect epidemiological dynamics but studies tend not to control for the overall heterogeneity in the number of secondary cases caused by an infection. To explore the role of individual variation in infection duration and transmission rate on parasite emergence and spread, while controlling for this potential bias, we simulate stochastic outbreaks with and without parasite evolution. As expected, heterogeneity in the number of secondary cases decreases the probability of outbreak emergence. Furthermore, for epidemics that do emerge, assuming more realistic infection duration distributions leads to faster outbreaks and higher epidemic peaks. When parasites require adaptive mutations to cause large epidemics, the impact of heterogeneity depends on the underlying evolutionary model. If emergence relies on within-host evolution, decreasing the infection duration variance decreases the probability of emergence. These results underline the importance of accounting for realistic distributions of infection rates to anticipate the effect of individual heterogeneity on epidemiological dynamics.

The expected number of secondary cases produced by an infected individual in a naive population is a key concept in epidemiology [6, 32]. It is classically referred to as the basic reproduction number and denoted R0. Only infections with R0 > 1 can cause major outbreaks. However, this mean value does not reflect the impact of super-spreading events, where an individual causes an unusually large number of secondary cases [19, 27, 36, 40, 44, 58]. The more frequent these events are, the higher the variance in the number of secondary cases, and, therefore, the lower the probability of outbreak emergence and the faster the epidemic growth for outbreaks that do emerge [40].

Several biological processes can explain the heterogeneity in the number of secondary cases [53]. However, models investigating these processes tend only to vary one source of heterogeneity at a time. By doing so, they do not control for the (overall) heterogeneity in the number of secondary cases, which is known to have strong effects, independently of its source [40]. One of the few exceptions suggests that the biology matters since it finds, for instance, that heterogeneity in host susceptibility has a lesser impact on the probability of emergence than heterogeneity in transmission rate, which can be defined as the product between a contact rate and the probability of transmission given that there is a contact between two individuals [59].

We use a stochastic mechanistic model to explore whether heterogeneity in transmission rates or recovery rates have different effects on an epidemic spread. Based on earlier models, we hypothesise that a more homogeneous distribution of infectious period duration decreases the variability of population dynamics in the early outbreak, therefore increasing the probability of outbreak extinction [5], but also increasing epidemic growth as well as epidemic peak size [5, 43]. However, we stress that these hypotheses are based on studies that, contrarily to us, do not control for variations in the distribution of the number of secondary cases.

Even if initially maladapted (i.e. R0 < 1), a parasite can evolve into a well-adapted strain before fading out and then cause a major outbreak, a phenomenon called ‘evolutionary emergence’ or ‘evolutionary rescue’ [8, 23]. Since higher epidemic sizes can be reached more frequently with increasing heterogeneity secondary cases when R0 < 1 [25], we hypothesise that the source of heterogeneity could affect evolutionary emergence. Since we do not explicitly model the within-host evolution process, we consider two extreme evolutionary processes for a mutant strain with R0 > 1 to appear [2, 23]: either by taking over a host infected by the resident strain or during a transmission event.

Following earlier studies [25, 29, 40], we assume that the number of secondary infections caused by each individual follows a Negative-Binomial distribution 𝒵 with mean R0 and dispersion parameter k. The smaller k, the more dispersed 𝒵. For example, the 2003 SARS outbreak in Singapore led to many superspreading events and transmission chain analyses estimated that k = 0.16 [40] and recent data from COVID-19 epidemics yielded values of k in the order of 0.3 [51].

We model individual transmission rates and infection duration values using lognormal distributions, denoted respectively ℬ and Γ. Most models involving ordinary differential equations are ‘memoryless’ -that is the duration of the infections is assumed to be exponentially distributed (CVΓ = 1) (but see [5, 39, 43]). This is biologically unrealistic for recovery events since they often depend on the number of days since infection [15, 37] and tends to overestimate the heterogeneity due to infection duration. We disentangle the specific role of infection duration heterogeneity from that of the secondary cases by varying k, and the coefficient of variation (CV) of the infection duration (CVΓ). Those two parameters combined govern the distribution of transmission rate.

We simulate outbreaks, without and with evolution, and measure key summary statistics to analyze the impact of different sources of heterogeneity on emerging outbreaks properties. We confirm that the dispersion of the distribution of the number of secondary infections (𝒵) is the main driver of the frequency of emergence, but we also find that the source of this heterogeneity has a strong impact on the properties of emerging epidemics, and more interestingly that it can affect the risk of evolutionary emergence.

As an illustration, we compare dynamics that could be obtained with parameters estimated from two outbreaks: SARS in Singapore in 2003 and Ebola in West Africa in 2014, which have similar values of R0 and k [4, 40] and different infection duration heterogeneity. We estimate CVΓ = 1.04 (95 % credible interval (CI): 0.44-1.9) for Ebola and 0.27 (95 % CI: 0.01 - 0.80) for SARS. An explanation for that difference is that the Ebola virus is known to sometimes persist in some body fluids after clearance from the blood [16]. Animal studies also show variability in the host immune response against Ebolavirus infection, which might allow persistence for some individuals [42]. Regarding SARS outbreaks, the reason why some infected individuals spread more than others the virus is thought to be a combination of host and environmental properties. On the biological side, individuals causing superspreading events were older [50], and coinfections have been hypothetised to increase the infectivity of SARS-CoV [11]. On the environmental side, superspreaders had a higher number of close contacts, and the diagnosis of the infection was often delayed [50].

Material and Methods

Model without evolution

We implement a non-Markovian version of the Susceptible-Infected-Recovered (SIR) epidemiological model [33], which means that not all rates are held constant throughout an infection [26]. We assume that the host population is of fixed size N and that epidemics are initiated by a single infectious individual. At time t, each individual is characterized by its current state (susceptible, infectious, or removed), and, if infected, the time at which it will recover.

The first source of heterogeneity in the model comes from the transmission rates and has a behavioural (i.e. contact rates) or a biological (i.e. infectiousness) origin. We model it by drawing the per capita transmission rate βi for each individual i from a lognormal distribution, denoted ℬ, with parameters μB and σB. For mathematical convenience, and without further qualitative impact, we set the mean of ℬ such that 𝔼 [B] N = 1. The standard deviation of ℬ is imposed by the choice of the coefficient of variation (CVB) which is equal 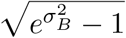Embedded Image.

The second source of heterogeneity comes from the infection duration and has a biological origin. We assume that individuals remain in the I compartment for a time drawn randomly from a lognormal distribution, noted Γ, with parameters μΓ and σΓ. By construction, the expectation of Γ is R0 in our model and we vary its coefficient of variation, which is equal to Embedded Image, between 0.05 and 2.

Coefficients of variation and 𝒵 dispersion

Given the construction of our model, the distribution od the number of secondary infections (𝒵) is determined by heterogeneities in transmission rate and infection duration. Since the force of infection over the course of an individual’s infection is the product of two lognormal distributions (ℬ and Γ), it is itself log-normally distributed, with parameters μZ = μB + μΓ and Embedded Image. 𝒵 is therefore a lognormal-Poisson compound distribution.

Evolutionary emergence model

We introduce an additional class of individuals by distinguishing between Ir and Im, which refer to individuals infected by the resident (resp. mutant) parasite strain, with reproduction number 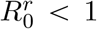Embedded Image (resp. 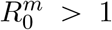Embedded Image). Initially, we assume that Ir = 1 and Im = 0. Mutant infections can emerge from a transmission event or from taking over an infected host. In the case of within-host mutation, the mutation rate represents the instantaneous probability that a mutant appears and takes over the host. In the case of mutation during transmission, it represents the probability that a mutant is transmitted instead of a resident strain. We assume that the mutation increases the mean transmission rate without altering CVB (i.e. by setting Embedded Image. We further assume that the infectious period duration is not impacted by the mutation. For simplicity, we neglect coinfections and therefore assume that, in the case of within-host mutations, the mutant instantaneously takes over the host.

Frequency of emergence

We use the total epidemic size to determine if an outbreak has emerged or not. Emergence is assumed to occur when the total epidemic size is greater than the herd immunity threshold, i.e. 1 −1/R0 [6].

Numerical simulations

We simulate epidemics, i.e. the succession of infection and recovery events, using Gillespie’s next reaction method [26] to generate non-Markovian distributions. The algorithm runs as follows:

  1. Initialize (i.e. set S, I = 1, t = 0)

  2. In case of new infected individual i, draw βi and the recovery time of this individual from the distribution Γ.

  3. Update the new force of infection Embedded Image and draw the time to the next infection assuming an exponential distribution.

  4. Look for the event with the closest time of occurrence (i.e. either recovery or new infection), and update the compartments (S, I).

  5. Update the time t to the time of the new event.

  6. Go back to step 2.

In case of evolutionary emergence, we adapt the model in function of the way the mutant appears. i) If the mutant appears during transmission, the model includes one force of infection for each class of infected host (Ir and Im), and two additional events: infection by the mutant strain (assuming an exponential distribution with a rate Embedded Image, and recovery of an Im individual. ii) In the scenario where the mutant first takes over the host, we distinguish the event of infection by the mutant strain (assuming an exponential distribution with a rate 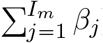Embedded Image) from the within-host mutation of a resident strain into a mutant strain (assuming an exponential distribution with a rate Ir × μ).

The model was implemented in Java 11.0.7 using parallel computation to decrease computing time. Simulation outputs were analyzed with R v.4.1.2. The scripts used are available at https://gitlab.in2p3.fr/ete/heterogeneity-outbreak.

Parameters estimation for known outbreaks

To estimate CVB and CVΓ from observed outbreaks, we analyzed serial interval and secondary cases distributions from Measles [31], Ebola [20, 57], pneumonic plague [24], Smallpox [21, 46], Monkeypox [30] and SARS outbreaks [38, 40]. For the Measles outbreak, patient line data were available, therefore allowing joint distribution estimations, and for the others, we had to assume that the two distributions were independent (see the Table S1 for further details about the data and parameters sources).

To obtain biologically relevant parameters from these empirical data, we infer parameters assuming a model with a latent period, the distribution of which we set using independent sources in the literature [9, 35, 45, 47, 57]. For simplicity, we assume that for a given parasite the distribution of the latent period does not vary between outbreaks. We also use independent estimates of R0 [31, 38, 57]. We also assume a constant transmission rate during infectious period. We use a Bayesian approach, with the following priors: CVB ∼ 𝒩 (2, 10) and CVΓ ∼ 𝒩 (0.5, 1). We use jags v. 4.3.0 to estimate parameters.

Results

Epidemics emergence without evolution

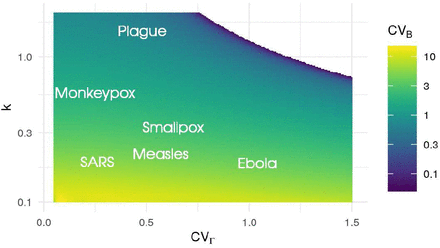
For a given secondary cases heterogeneity k, the coefficients of variation in infection duration (CVΓ) and transmission rate (CVB) are negatively correlated. This is shown in Figure 1 and further explained in the Methods. The former being easier to measure, we focus on the role of infection duration heterogeneity, but the results can also be interpreted in terms of infectivity heterogeneity.

Figure 1:
Figure 1: Numerical estimation of the infection rate coefficient of variation (CVB), as a function of k and CVΓ.

Names in white show the range of values estimated using maximum likelihood methods from outbreak data. If k remains constant, increasing CVΓ always decreases CVB. Note that when secondary cases heterogeneity is low (i.e. k is high) it is impossible to have a high CVΓ.

To illustrate the feasibility to infer these infection properties, we highlight the parameter value for several well-studied outbreaks in Figure 1. This also shows that our parameters ranges are biologically realistic.

Probability of emergence

Figure 2A shows that the probability of an outbreak emergence only depends on the overall 𝒵 heterogeneity, here measured by k. The source of heterogeneity (i.e. infection duration or infectiousness) does not seem to play any role. Results are shown with R0 = 1.5, but a similar pattern is observed for any R0 < 1.

Figure 2:
Figure 2: Summary statistics of epidemics emergence without evolution.

A) Frequency of emergence of an outbreak starting from one infection as a function of model heterogeneity, with R0 = 1.5. B) Epidemic trajectories with the same secondary cases distribution k = 0.4, but different infection duration heterogeneity (CVΓ = 1 in brown and CVΓ = 0.5 in red). The total population size is 50,000.

C) Relative time until the epidemic reaches the emergence threshold (i.e. here a prevalence of 100 infected individuals). D) Relative doubling time during the exponential phase (i.e. going from a prevalence of 500 to 1000 infections). E) Relative prevalence peak size. F) Final outbreak size, as a percentage of the total population. Panels C, D, and E show metrics relative to the case where k = 1 and CVΓ = 1, and colors indicate the value of CVΓ. Lines represent mean values computed from simulated outbreaks that emerged and shaded areas the 95% confidence interval.

In the following, we analyze the properties of simulated outbreaks without evolution with R0 = 1.5 and compare key metrics to a reference value close to the markovian case, i.e. k = 1 and CVΓ = 1.

Growth rate

In the initial phases of an outbreak, the law of large numbers does not apply and prevalence time series shown are strongly affected by stochasticity (Fig. 2B). We quantify the early growth during this stochastic phase by measuring the time until the prevalence reaches the outbreak threshold of 100 infected individuals [28]. As expected [40], decreasing k leads to faster epidemic growth. Furthermore, for a given k, increasing the heterogeneity in infection duration also increases the early epidemic growth (Fig. 2C). On average, this would make a SARS outbreak reach the outbreak threshold 50% faster than an Ebola outbreak.

We then study the deterministic exponential growth phase, which starts when the number of infected is high enough to reach the law of large numbers, and ends when the depletion of susceptible host population cannot be neglected anymore [28] (Fig. 2B). Figure 2D shows that the growth rate during this phase is mostly impacted by CVΓ. For instance, even with similar R0, Ebola outbreaks would have a doubling time of 1.4 times the mean infection duration, while SARS outbreaks would have a doubling time of 0.9 time the mean infection duration. Not taking into account the difference in infectious period distribution between the two epidemics and considering a memoryless model with CVΓ =)1 would lead to an overestimation of the SARS R0 [55].

Epidemic peak size and final size

The prevalence peak value is highly affected by the heterogeneity in infection duration: its median increases by more than 50% when CVΓ decreases from 1 to 0.5 (Fig. 2 E). k has little effect on the mean epidemic peak size, but there is a correlation between the variance in peak size and that of 𝒵.

Finally, none of our heterogeneity metric seems to affect the median final epidemic size, which is always close to 58% of the population (Fig. 2 F), corresponding to the expected value for R0 = 1.5 according to classical theory [33]. As for the other metrics, the variance in the total epidemic size decreases with k.

Evolutionary emergence

We now assume that the introduced ‘resident’ strain has a 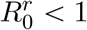Embedded Image and, therefore, will go extinct unless it evolves into a phenotypically different ‘mutant’ strain with 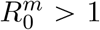Embedded Image. The mutant strain can arise either by taking over a host infected by the resident strain or during a transmission event.

Mutation probability

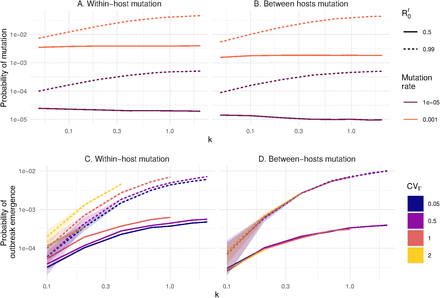
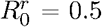To disentangle the evolutionary process from the epidemiological process, following Yates et al.[59], we first assume that a mutant instantaneously takes over the population Embedded Image. The probability of mutant emergence does not depend on the origin of heterogeneity. Moreover, figures 3A and B show that the way the mutant strain appears does not seem to affect the relationship between the frequency of emergence and the secondary cases heterogeneity k: when Embedded Image, there is little impact of k on the frequency of emergence, whereas when 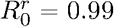Embedded Image, increasing k increases the frequency of emergence.

Figure 3:
Figure 3: Individual heterogeneity and evolutionary emergence.

Probability of mutation, as a function of the mutation origin, mutation rate and 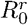Embedded Image. A) the mutant appears during the infection within a host and replaces the resident strain, or B) the mutant appears during transmission. Since there is no difference in function of CVΓ, the results shown combine the whole range of CVΓ.

Probability of outbreak emergence of a mutant C) taking over a host and D) appearing during transmission, in the case 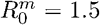Embedded Image and a mutation rate of 10−3.

Mutant outbreak

We then consider the more realistic case where the mutant has a R0 = 1.5 (Fig. 3C, D). The general trend is qualitatively consistent with the case without evolution: decreasing the secondary cases heterogeneity increases the frequency of emergence.

When the mutant appears during transmission (Fig. 3D), the source of heterogeneity does not play any role. However, when the mutant appears by taking over an infection (Fig. 3C), decreasing the infection duration heterogeneity increases the probability of emergence. The difference between these two scenarios is that when the mutant arises within the host, the infection is ongoing, and the host recovery time is kept constant since we assume no difference in immune response between resident and variant strains. Therefore, with a more heterogeneous infection duration, individuals with longer infections will increase the probability that a mutant arises within the host and can transmit before the host recovery.

Discussion

When modeling epidemics, the variation between individuals can be aggregated into a single metric, the dispersion of the secondary infections caused by each individual, which shapes infectious diseases outbreaks [40]. Several studies investigate how variations in a specific trait can have an impact on epidemiological dynamics but the majority overlook that variations in one trait (e.g. the distribution of the duration of infectious periods) may also affect the distribution of individual secondary cases. In this study, we investigate the relative effects of variation in the infection duration and transmission rate while keeping the distribution of the secondary cases constant.

Increasing the heterogeneity in transmission rates is known to lead to a faster increase in cases per generation among the outbreaks that do emerge in branching process models [40]. By simulating the whole course of the epidemic, we show that this effect does not translate into an increased growth rate after the epidemic evades the stochastic phase. Methodologically, this could also be studied using recent developments of branching process theory in epidemiology to incorporate the depletion of susceptible hosts [10].

We show that the heterogeneity in infectious period duration plays an important role in the deterministic phase of the epidemic, by increasing the growth rate and, more strikingly, the prevalence peak size. While previous studies reported a similar effect on both secondary cases heterogeneity and infection duration heterogeneity [5, 13, 55, 56], we further show that this phenomenon is intrinsically related to the latter. Indeed, more heterogeneous infectious periods are known to lead to longer generation times because transmission relies on long infections, therefore increasing the doubling time and flattening the epidemic curve [55].

When considering a simple evolutionary rescue scenario, we show that the probability of mutation does not depend on the infection duration heterogeneity. This is consistent with the observation that the final epidemic size is not affected by the source of heterogeneity. Furthermore, we show that with very low 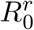Embedded Image, secondary cases distribution does not have any impact either. This can be explained by the fact that for R0 < 1, the decrease in frequency of emergence associated with heterogeneity is compensated by a higher probability in reaching larger outbreak sizes [25] (Fig. S1), therefore maintaining the mean outbreak size (Fig. S2). This effect diminishes as R0 gets higher and disappears when R0 > 1.

Finally, we show that infectious period duration heterogeneity can affect evolutionary emergence depending on the process that generates the mutant infection [23]. The impact of the mutational pathway and evolutionary scenario has already been pointed out by several studies [1, 59]. As expected, we find no difference between the two mutation scenarios if the process is memoryless. This further underlines the importance of questioning this biologically-unrealistic assumption [5, 13, 39, 43]. When assuming more realistic infection duration distributions, we find that if mutations appear upon transmission events, the probability of evolutionary emergence only depends on the distribution of the secondary cases. However, when the mutation appears after a host takeover, infection duration heterogeneity increases the frequency of emergence. This is illustrated by figure S4: although in either scenario the probability that a mutant appears remains constant and equal to the mutation rate, when the mutation occurs within the host, the probability that it gets transmitted is higher in the case of rare long infections, as already pointed out [7].

Our effort to maintain a simple and tractable model of outbreak emergence naturally leads to several limitations. In particular, there is an identifiability issue regarding the biological bases of the transmission rate heterogeneity, which could originate from variations in transmission rate or in host susceptibility. However, Yates et al. [59] find that the heterogeneity in infectivity plays a larger role in the frequency of emergence than the heterogeneity in susceptibility. It could also be interesting to enrich the model by considering a latent period during which exposed hosts are not yet infectious. This has been shown to affect R0 estimates but in a deterministic model that did not take into account superspreading events [56]. More generally, investigating other sources of heterogeneity of the number of secondary infections may help uncover potential biases. Another simplification made here is the assumption that infectiousness is constant over the infectious period of and individual. This is biologically not true, and therefore the infectious period defined here is probably shorter than the real infectious period, since infectiousness is usually higher at the beginning of the epidemic.

Since we ignore within-host dynamics, we chose two extreme scenarios regarding the way a mutant appears: either during transmission or within the host. Biological reality is likely in-between: mutants will gradually take over a host, which means an increasing proportion of the transmission events will be caused by the mutant [2]. At least for rapidly evolving viruses such as HIV-1 and HCV, within-host genetic variation is higher than what is expected given the strong host immune response selection [49]. This shows that within-host selection of novel mutations and transmission occur at the same rate.

Nested models, which explicitly include both within and between-host dynamics, can take into account this gradual replacement. Coombs et alii [17] showed in a simple nested model with chronic infections that the best between-hosts competitors can be competitively excluded if they are outcompeted within the host in the short term during an infection. Moreover, when allowing mutation, coexistence of both strains could be possible under certain scenarios, which was not possible with our simplified model. When taking explicitly into account the interaction between the parasite and the host’s immune system and the possibility of multiple infections, models suggest that the outcome of the competition can lead to the coexistence of two strains with different within-host growth rates, as soon as there is a possibility that multiple infections can occur [3]. Including the possibility that more than two strains can coexist during the infection, it was shown that the level of selection that matters depends on the extent of phenotypic variation: with a higher between-host than within-host phenotypic variation is observed, it is expected that strains maximizing the between-host transmission are selected, and vice-versa [41]. Finally, Park et alii [48] combined a nested model with the question of the probability of emergence of an outbreak, with a stochastic epidemiological model. They showed that conflicting fitness effects of a mutation at the within-host level and at the between-host levels can strongly decrease the probability of emergence of a mutant.

We assumed that the population has no spatial structure, which is more realistic for directly transmitted diseases, such as SARS or measles, than for sexually transmitted infections for which contact networks impose strong constraints [25]. Furthermore, at the beginning of an epidemic, the spatial structure appears to have little effect on outbreak metrics, especially R0 [52]. However, it is known that heterogeneity in host susceptibility and spatial structure decrease the final epidemic size, i.e. the total proportion of the population infected throughout the epidemic [12, 54]. We also do not include host demography and limit our analysis to a single epidemic wave.

We also assumed no correlation between infectiousness and infectious period duration. While this seems biologically realistic, little is known about the nature of the relationship between those parameters. Indeed, one could expect that higher infectiousness is associated with a higher pathogen load, leading to a shorter asymptomatic period where transmission can occur, as it has been observed for HIV infections [22]. However, when analyzing the Measles outbreak from Hagelloch, where a joint estimation of both parameters is possible, we found no significant correlation between the estimated infectious rate and the infectious period duration (Fig. S3), although our sample is limited to the 32 individuals who did transmit early in the outbreak.

Finally, this analysis relies on numerical results. This enables us to explore the role of stochasticity, which is particularly important to consider in the context of outbreak emergence from a mathematical modelling [14] and a statistical inference [34] point of view. However, it limits our analysis to the area of punctual parameters that we selected as being biologically relevant.

These theoretical results have implications for outbreak monitoring. In particular, we show that making simplifying but biologically unrealistic assumptions about the distributions of infection duration can lead to underestimating the risk of emergence, the epidemic doubling time, and the prevalence peak size. Given the risk of saturation of healthcare systems, accurately anticipating these values is a major issue. This stresses the importance of collecting detailed biological data to better inform epidemiological models.

Acknowledgements

The authors thank the CNRS, the IRD, and acknowledge the itrop HPC (South Green Platform) at IRD Montpellier for providing HPC resources that have contributed to the research results reported within this study (https://bioinfo.ird.fr/).

This paper has been submitted on a preprint server [18].

Footnotes

  • Resubmission of the manuscript taking into account the reviewer's comments.

References

  1. [1].↵
    Alexander, H. K. & Day, T., 2010 Risk factors for the evolutionary emergence of pathogens. Journal of The Royal Society Interface 7, 1455–1474. (doi: 10.1098/rsif.2010.0123).
    OpenUrlCrossRefPubMed
  2. [2].↵
    Alizon, S., Luciani, F. & Regoes, R. R., 2011 Epidemiological and clinical consequences of within-host evolution. Trends in Microbiology 19, 24–32. (doi: 10.1016/j.tim.2010.09.005).
    OpenUrlCrossRefPubMedWeb of Science
  3. [3].↵
    Alizon, S. & van Baalen, M., 2008 Multiple Infections, Immune Dynamics, and the Evolution of Virulence. The American Naturalist 172, E150–E168. (doi: 10.1086/590958).
    OpenUrlCrossRefPubMedWeb of Science
  4. [4].↵
    Althaus, C. L., 2015 Ebola superspreading. The Lancet Infectious Diseases 15, 507–508. (doi: 10.1016/S1473-3099(15)70135-0).
    OpenUrlCrossRef
  5. [5].↵
    Anderson, D. & Watson, R., 1980 On the spread of a disease with gamma distributed latent and infectious periods. Biometrika 67, 191–198. (doi: 10.1093/biomet/67.1.191).
    OpenUrlCrossRefWeb of Science
  6. [6].↵
    Anderson, R. M. & May, R. M., 1992 Infectious Diseases of Humans: Dynamics and Control. United Kingdom: Oxford Univ. Press, original edn.
  7. [7].↵
    André, J.-B. & Day, T., 2005 The effect of disease life history on the evolutionary emergence of novel pathogens. Proceedings of the Royal Society B: Biological Sciences 272, 1949–1956. (doi: 10.1098/rspb.2005.3170).
    OpenUrlCrossRefPubMedWeb of Science
  8. [8].↵
    Antia, R., Regoes, R. R., Koella, J. C. & Bergstrom, C. T., 2003 The role of evolution in the emergence of infectious diseases. Nature 426, 658–661. (doi: 10.1038/nature02104).
    OpenUrlCrossRefPubMedWeb of Science
  9. [9].↵
    Bailey, N. T. J., 1956 On Estimating the Latent and Infectious Periods of Measles: I. Families with Two Susceptibles Only. Biometrika 43, 15. (doi: 10.2307/2333574).
    OpenUrlCrossRefWeb of Science
  10. [10].↵
    Barbour, A. & Reinert, G., 2013 Approximating the epidemic curve. Electronic Journal of Probability 18. (doi: 10.1214/EJP.v18-2557).
    OpenUrlCrossRef
  11. [11].↵
    Bassetti, S., Bischoff, W. E. & Sherertz, R. J., 2005 Are SARS Superspreaders Cloud Adults? Emerging Infectious Diseases 11, 637–638. (doi: 10.3201/eid1104.040639).
    OpenUrlCrossRefPubMedWeb of Science
  12. [12].↵
    1. J.-P. Gabriel,
    2. C. Lefèvre &
    3. P. Picard
    Becker, N. & Marschner, I., 1990 The effect of heterogeneity on the spread of disease. In Stochastic Processes in Epidemic Theory (eds. J.-P. Gabriel, C. Lefèvre & P. Picard), pp. 90–103. Berlin, Heidelberg: Springer Berlin Heidelberg.
  13. [13].↵
    Britton, T. & Lindenstrand, D., 2008 Epidemic modelling: Aspects where stochasticity matters. arxiv:0812.3505 [math, q-bio].
  14. [14].↵
    Britton, T. & Pardoux, E., 2019 Stochastic epidemics in a homogeneous community. arxiv:1808.05350 [math] 2255. (doi: 10.1007/978-3-030-30900-8).
    OpenUrlCrossRef
  15. [15].↵
    Chan, M. & Johansson, M. A., 2012 The Incubation Periods of Dengue Viruses. PLoS ONE 7, e50972. (doi: 10.1371/journal.pone.0050972).
    OpenUrlCrossRefPubMed
  16. [16].↵
    Chughtai, A. A., Barnes, M. & Macintyre, C. R., 2016 Persistence of Ebola virus in various body fluids during convalescence: Evidence and implications for disease transmission and control. Epidemiology & Infection 144, 1652–1660. (doi: 10.1017/S0950268816000054).
    OpenUrlCrossRefPubMed
  17. [17].↵
    Coombs, D., Gilchrist, M. A. & Ball, C. L., 2007 Evaluating the importance of within- and between-host selection pressures on the evolution of chronic pathogens. Theoretical Population Biology 72, 576–591. (doi: 10.1016/j.tpb.2007.08.005).
    OpenUrlCrossRefPubMedWeb of Science
  18. [18].↵
    Elie, B., Selinger, C. & Alizon, S., 2021 The source of individual heterogeneity shapes infectious disease outbreaks. medRxiv p. 2021.02.18.21251983. (doi: 10.1101/2021.02.18.21251983).
    OpenUrlAbstract/FREE Full Text
  19. [19].↵
    Endo, A., Centre for the Mathematical Modelling of Infectious Diseases COVID-19 Working Group, Abbott, S., Kucharski, A. J. & Funk, S., 2020 Estimating the overdispersion in COVID-19 transmission using outbreak sizes outside China. Wellcome Open Research 5, 67. (doi: 10.12688/wellcomeopenres.15842.1).
    OpenUrlCrossRef
  20. [20].↵
    Faye, O., Boëlle, P.-Y., Heleze, E., Faye, O., Loucoubar, C., Magassouba, N., Soropogui, B., Keita, S., Gakou, T., Bah, E. H. I., Koivogui, L., Sall, A. A. & Cauchemez, S., 2015 Chains of transmission and control of Ebola virus disease in Conakry, Guinea, in 2014: An observational study. The Lancet Infectious Diseases 15, 320–326. (doi: 10.1016/S1473-3099(14)71075-8).
    OpenUrlCrossRefPubMed
  21. [21].↵
    Fenner, F., Henderson, D. A., Arita, I., Jezek, Z., Ladnyi, I. D. & Organization, W. H., 1988 Smallpox and Its Eradication. World Health Organization.
  22. [22].↵
    Fraser, C., Hollingsworth, T. D., Chapman, R., de Wolf, F. & Hanage, W. P., 2007 Variation in HIV-1 set-point viral load: Epidemiological analysis and an evolutionary hypothesis. Proceedings of the National Academy of Sciences 104, 17441–17446. (doi: 10.1073/pnas.0708559104).
    OpenUrlAbstract/FREE Full Text
  23. [23].↵
    Gandon, S., Hochberg, M. E., Holt, R. D. & Day, T., 2013 What limits the evolutionary emergence of pathogens? Philosophical Transactions of the Royal Society B: Biological Sciences 368, 20120086. (doi: 10.1098/rstb.2012.0086).
    OpenUrlCrossRefPubMed
  24. [24].↵
    Gani, R. & Leach, S., 2004 Epidemiologic Determinants for Modeling Pneumonic Plague Outbreaks. Emerging Infectious Diseases 10, 608–614. (doi: 10.3201/eid1004.030509).
    OpenUrlCrossRefPubMedWeb of Science
  25. [25].↵
    Garske, T. & Rhodes, C., 2008 The effect of superspreading on epidemic outbreak size distributions. Journal of Theoretical Biology 253, 228–237. (doi: 10.1016/j.jtbi.2008.02.038).
    OpenUrlCrossRefPubMedWeb of Science
  26. [26].↵
    Gibson, M. A. & Bruck, J., 2000 Efficient Exact Stochastic Simulation of Chemical Systems with Many Species and Many Channels. The Journal of Physical Chemistry A 104, 1876–1889. (doi: 10.1021/jp993732q).
    OpenUrlCrossRefWeb of Science
  27. [27].↵
    Gomes, M. G. M., Águas, R., Lopes, J. S., Nunes, M. C., Rebelo, C., Rodrigues, P. & Struchiner, C. J., 2012 How host heterogeneity governs tuberculosis reinfection? Proceedings of the Royal Society B: Biological Sciences 279, 2473–2478. (doi: 10.1098/rspb.2011.2712).
    OpenUrlCrossRefPubMed
  28. [28].↵
    Hartfield, M. & Alizon, S., 2014 Epidemiological Feedbacks Affect Evolutionary Emergence of Pathogens. The American Naturalist 183, E105–E117. (doi: 10.1086/674795).
    OpenUrlCrossRef
  29. [29].↵
    Hellewell, J., Abbott, S., Gimma, A., Bosse, N. I., Jarvis, C. I., Russell, T. W., Munday, J. D., Kucharski, A. J., Edmunds, W. J., Funk, S., Eggo, R. M., Sun, F., Flasche, S., Quilty, B. J., Davies, N., Liu, Y., Clifford, S., Klepac, P., Jit, M., Diamond, C., Gibbs, H. & van Zandvoort, K., 2020 Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. The Lancet Global Health 8, e488–e496. (doi: 10.1016/S2214-109X(20)30074-7).
    OpenUrlCrossRef
  30. [30].↵
    Jezek, Z., Grab, B. & Dixon, H., 1987 Stochastic model for interhuman spread of Monkeypox. American Journal of Epidemiology 126, 1082–1092. (doi: 10.1093/oxfordjournals.aje.a114747).
    OpenUrlCrossRefPubMedWeb of Science
  31. [31].↵
    Jombart, T., Frost, S., Nouvellet, P., Campbell, F. & Sudre, B., 2020 Outbreaks: A Collection of Disease Outbreak Data.
  32. [32].↵
    Keeling, M. J. & Rohani, P., 2008 Modeling Infectious Diseases in Humans and Animals. Princeton University Press.
  33. [33].↵
    Kermack, W. O. & McKendrick, A. G., 1927 A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London. Series A 115, 700–721. (doi: 10.1098/rspa.1927.0118).
    OpenUrlCrossRef
  34. [34].↵
    King, A. A., Domenech de Cellès, M., Magpantay, F. M. G. & Rohani, P., 2015 Avoidable errors in the modelling of outbreaks of emerging pathogens, with special reference to Ebola. Proceedings of the Royal Society B: Biological Sciences 282, 20150347. (doi: 10.1098/rspb.2015.0347).
    OpenUrlCrossRefPubMed
  35. [35].↵
    Kuk, A. Y. C. & Ma, S., 2005 The estimation of SARS incubation distribution from serial interval data using a convolution likelihood. Statistics in Medicine 24, 2525–2537. (doi: 10.1002/sim.2123).
    OpenUrlCrossRefPubMed
  36. [36].↵
    Lemieux, J. E., Siddle, K. J., Shaw, B. M., Loreth, C., Schaffner, S. F., Gladden-Young, A., Adams, G., Fink, T., Tomkins-Tinch, C. H., Krasilnikova, L. A., DeRuff, K. C., Rudy, M., Bauer, M. R., Lagerborg, K. A., Normandin, E., Chapman, S. B., Reilly, S. K., Anahtar, M. N., Lin, A. E., Carter, A., Myhrvold, C., Kemball, M. E., Chaluvadi, S., Cusick, C., Flowers, K., Neumann, A., Cerrato, F., Farhat, M., Slater, D., Harris, J. B., Branda, J. A., Hooper, D., Gaeta, J. M., Baggett, T. P., O’Connell, J., Gnirke, A., Lieberman, T. D., Philippakis, A., Burns, M., Brown, C. M., Luban, J., Ryan, E. T., Turbett, S. E., LaRocque, R. C., Hanage, W. P., Gallagher, G. R., Madoff, L. C., Smole, S., Pierce, V. M., Rosenberg, E., Sabeti, P. C., Park, D. J. & MacInnis, B. L., 2021 Phylogenetic analysis of SARS-CoV-2 in Boston highlights the impact of superspreading events. Science 371, eabe3261. (doi: 10.1126/science.abe3261).
    OpenUrlAbstract/FREE Full Text
  37. [37].↵
    Lessler, J., Reich, N. G., Brookmeyer, R., Perl, T. M., Nelson, K. E. & Cummings, D. A., 2009 Incubation periods of acute respiratory viral infections: A systematic review. The Lancet Infectious Diseases 9, 291–300. (doi: 10.1016/S1473-3099(09)70069-6).
    OpenUrlCrossRefPubMedWeb of Science
  38. [38].↵
    Lipsitch, M., Cohen, T., Cooper, B., Robins, J. M., Ma, S., James, L., Gopalakrishna, G., Chew, S. K., Tan, C. C., Samore, M. H., Fisman, D. & Murray, M., 2003 Transmission Dynamics and Control of Severe Acute Respiratory Syndrome. Science 300, 6.
    OpenUrl
  39. [39].↵
    Lloyd, A. L., 2001 Realistic Distributions of Infectious Periods in Epidemic Models: Changing Patterns of Persistence and Dynamics. Theoretical Population Biology 60, 59–71. (doi: 10.1006/tpbi.2001.1525).
    OpenUrlCrossRefPubMedWeb of Science
  40. [40].↵
    Lloyd-Smith, J. O., Schreiber, S. J., Kopp, P. E. & Getz, W. M., 2005 Superspreading and the effect of individual variation on disease emergence. Nature 438, 355–359. (doi: 10.1038/nature04153).
    OpenUrlCrossRefPubMedWeb of Science
  41. [41].↵
    Lythgoe, K. A., Pellis, L. & Fraser, C., 2013 Is Hiv Short-Sighted? Insights from a Multistrain Nested Model. Evolution 67, 2769–2782. (doi: 10.1111/evo.12166).
    OpenUrlCrossRefPubMedWeb of Science
  42. [42].↵
    MacIntyre, C. R. & Chughtai, A. A., 2016 Recurrence and reinfection—a new paradigm for the management of Ebola virus disease. International Journal of Infectious Diseases 43, 58–61. (doi: 10.1016/j.ijid.2015.12.011).
    OpenUrlCrossRefPubMed
  43. [43].↵
    Malice, M.-P. & Kryscio, R. J., 1989 On the Role of Variable Incubation Periods in Simple Epidemic Models. Mathematical Medicine and Biology 6, 233–242. (doi: 10.1093/imammb/6.4.233).
    OpenUrlCrossRefPubMed
  44. [44].↵
    Marm Kilpatrick, A., Daszak, P., Jones, M. J., Marra, P. P. & Kramer, L. D., 2006 Host heterogeneity dominates West Nile virus transmission. Proceedings of the Royal Society B: Biological Sciences 273, 2327–2333. (doi: 10.1098/rspb.2006.3575).
    OpenUrlCrossRefPubMedWeb of Science
  45. [45].↵
    Nishiura, H., 2009 Determination of the appropriate quarantine period following smallpox exposure: An objective approach using the incubation period distribution. International Journal of Hygiene and Environmental Health 212, 97–104. (doi: 10.1016/j.ijheh.2007.10.003).
    OpenUrlCrossRefPubMed
  46. [46].↵
    Nishiura, H. & Eichner, M., 2007 Infectiousness of smallpox relative to disease age: Estimates based on transmission network and incubation period. Epidemiology and Infection 135, 1145–1150. (doi: 10.1017/S0950268806007618).
    OpenUrlCrossRefPubMed
  47. [47].↵
    Nolen, L. D., Osadebe, L., Katomba, J., Likofata, J., Mukadi, D., Monroe, B., Doty, J., Hughes, C. M., Kabamba, J., Malekani, J., Bomponda, P. L., Lokota, J. I., Balilo, M. P., Likafi, T., Lushima, R. S., Ilunga, B. K., Nkawa, F., Pukuta, E., Karhemere, S., Tamfum, J.-J. M., Nguete, B., Wemakoy, E. O., McCollum, A. M. & Reynolds, M. G., 2016 Extended Human-to-Human Transmission during a Monkeypox Outbreak in the Democratic Republic of the Congo. Emerging Infectious Diseases 22, 1014–1021. (doi: 10.3201/eid2206.150579).
    OpenUrlCrossRef
  48. [48].↵
    Park, M., Loverdo, C., Schreiber, S. J. & Lloyd-Smith, J. O., 2013 Multiple scales of selection influence the evolutionary emergence of novel pathogens. Philosophical Transactions of the Royal Society B: Biological Sciences 368, 20120333. (doi: 10.1098/rstb.2012.0333).
    OpenUrlCrossRefPubMed
  49. [49].↵
    Poon, A. F. Y., Pond, S. L. K., Bennett, P., Richman, D. D., Brown, A. J. L. & Frost, S. D. W., 2007 Adaptation to Human Populations Is Revealed by Within-Host Polymorphisms in HIV-1 and Hepatitis C Virus. PLOS Pathogens 3, e45. (doi: 10.1371/journal.ppat.0030045).
    OpenUrlCrossRefPubMed
  50. [50].↵
    Shen, Z., Ning, F., Zhou, W., He, X., Lin, C., Chin, D. P., Zhu, Z. & Schuchat, A., 2004 Superspreading SARS Events, Beijing, 2003. Emerging Infectious Diseases 10, 256–260. (doi: 10.3201/eid1002.030732).
    OpenUrlCrossRefPubMedWeb of Science
  51. [51].↵
    Sun, K., Wang, W., Gao, L., Wang, Y., Luo, K., Ren, L., Zhan, Z., Chen, X., Zhao, S., Huang, Y., Sun, Q., Liu, Z., Litvinova, M., Vespignani, A., Ajelli, M., Viboud, C. & Yu, H., 2021 Transmission heterogeneities, kinetics, and controllability of SARS-CoV-2. Science 371. (doi: 10.1126/science.abe2424).
    OpenUrlAbstract/FREE Full Text
  52. [52].↵
    Trapman, P., Ball, F., Dhersin, J.-S., Tran, V. C., Wallinga, J. & Britton, T., 2016 Inferring R <sub>0</sub> in emerging epidemics—the effect of common population structure is small. Journal of The Royal Society Interface 13, 20160288. (doi: 10.1098/rsif.2016.0288).
    OpenUrlCrossRefPubMed
  53. [53].↵
    VanderWaal, K. L. & Ezenwa, V. O., 2016 Heterogeneity in pathogen transmission: Mechanisms and methodology. Functional Ecology 30, 1606–1622. (doi: 10.1111/1365-2435.12645).
    OpenUrlCrossRef
  54. [54].↵
    Volz, E., 2008 SIR dynamics in random networks with heterogeneous connectivity. Journal of Mathematical Biology 56, 293–310. (doi: 10.1007/s00285-007-0116-4).
    OpenUrlCrossRefPubMedWeb of Science
  55. [55].↵
    Wallinga, J. & Lipsitch, M., 2007 How generation intervals shape the relationship between growth rates and reproductive numbers. Proceedings of the Royal Society B: Biological Sciences 274, 599–604.
    OpenUrlCrossRefPubMedWeb of Science
  56. [56].↵
    Wearing, H. J., Rohani, P. & Keeling, M. J., 2005 Appropriate Models for the Management of Infectious Diseases. PLoS Medicine 2, e174. (doi: 10.1371/journal.pmed.0020174).
    OpenUrlCrossRefPubMed
  57. [57].↵
    WHO Ebola Response Team, 2014 Ebola Virus Disease in West Africa — The First 9 Months of the Epidemic and Forward Projections. New England Journal of Medicine 371, 1481–1495. (doi: 10.1056/NEJMoa1411100).
    OpenUrlCrossRefPubMed
  58. [58].↵
    Woolhouse, M. E. J., Dye, C., Etard, J.-F., Smith, T., Charlwood, J. D., Garnett, G. P., Hagan, P., Hii, J. L. K., Ndhlovu, P. D., Quinnell, R. J., Watts, C. H., Chandiwana, S. K. & Anderson, R. M., 1997 Heterogeneities in the transmission of infectious agents: Implications for the design of control programs. Proceedings of the National Academy of Sciences 94, 338–342. (doi: 10.1073/pnas.94.1.338).
    OpenUrlAbstract/FREE Full Text
  59. [59].↵
    Yates, A., Antia, R. & Regoes, R. R., 2006 How do pathogen evolution and host heterogeneity interact in disease emergence? Proceedings of the Royal Society B: Biological Sciences 273, 3075–3083. (doi: 10.1098/rspb.2006.3681).
    OpenUrlCrossRefPubMedWeb of Science
Back to top
Posted February 07, 2022.
Download PDF

Supplementary Material

Data/Code
Email
The source of individual heterogeneity shapes infectious disease outbreaks
Baptiste Elie, Christian Selinger, Samuel Alizon
medRxiv 2021.02.18.21251983; doi: https://doi.org/10.1101/2021.02.18.21251983
Twitter logo Facebook logo LinkedIn logo Mendeley logo
Citation Tools

Subject Area