A major population resource of 474,074 participants in UK Biobank to investigate determinants and biomedical consequences of leukocyte telomere length

LTL measurements in 488,400 participants

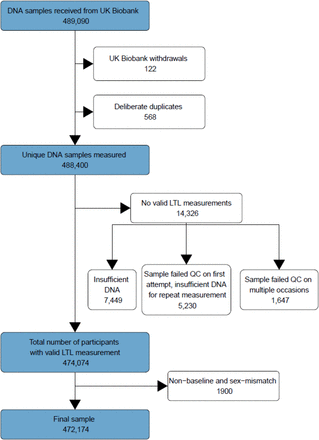
Of the 489,090 DNA samples received by our laboratory from UKB, 488,400 remained after removal of duplicates and samples from participants who had withdrawn from the study (Methods; Figure 1). Valid LTL measurements were obtained for 474,074 (97.1%) samples. Of the 14,326 (2.9%) participants without a valid LTL measurement, the large majority had insufficient DNA, with only 1647 repeatedly failing LTL assay QC (Figure 1). A small proportion of participants had LTL measured in DNA samples not collected at baseline (Figure 1).

• Download figure
• Open in new tab

Figure 1. DNA sample workflow to derive the final dataset.

After removal of study withdrawals and deliberate duplicate samples there were 488,400 participants for whom we attempted to measure LTL. Either a valid measurement was obtained or the sample was attributed to one of three categories of failure. For the downstream analyses presented in this paper that related to baseline phenotypes, we removed 1,900 DNA samples whose LTL was measured in a non-baseline DNA sample or where self-reported sex and genetic sex did not match.

Using multivariable regression models, we assessed the contribution of nine technical parameters to LTL variability, of which six had significant associations (Table 1 and Supplementary Figure 1). PCR machine (Rotor-Gene Q), explained the greatest proportion of LTL variation in the multivariable model, followed by enzyme batch, temperature, staff member (operator), primer batch, and humidity. No associations were observed for the time of day of assay runs, pipetting robot (Qiagility) or DNA extraction method. We then considered all possible pairwise interactions and identified statistically significant interactions of primer batch with each of operator and PCR machine (Table 1 and Supplementary Figure 2). In combination, the significant technical parameters and interactions explained 23.7% of LTL variation. Further, we estimated that the A260/280 ratio (a measure of DNA purity) explained an additional 0.5% of LTL variation (Supplementary Figure 3).

To assess the impact of adjusting LTL for the relevant technical parameter mentioned above, we considered the mean LTL per week over the four-year assay period (Figure 2). While the unadjusted LTL measurements showed substantial fluctuations over time (Figure 2A), the adjusted LTL measurements were much more consistent across the assay period (Figure 2B). Adjustment strengthened the inverse correlation of LTL with age from −0.185 to −0.195 and increased the variance in LTL explained by age and sex from 4.04% to 4.53% (see further analyses below). Except when stated otherwise, the remaining analyses in this report used LTL values adjusted for technical parameters.

• Download figure
• Open in new tab

Figure 2. Distribution of weekly average LTL across duration of the study.

A) The unadjusted LTL trend over time (and 95% confidence band). B) The adjusted LTL trend over time (and 95% confidence band). Adjustments for enzyme, PCR machine, primer, Operator, temperature, humidity, primer*PCR machine, primer*Operator and A260/280 were made as described in Methods. The smoothed curve is based on half plate means, with plotted data points representing overall weekly means. The size of each point indicates the number of runs that week. There were fewer measurements made after week 175, reflecting the period that sample QC and re-measurements took precedence following QC checks towards the end of the project.

Reproducibility of LTL measurements

To assess our assay’s reproducibility, we calculated the coefficient of variation (CV) using samples measured on two separate occasions. For the blinded duplicates (n=528) included by UKB, the distribution of CVs was strongly positively skewed (Supplementary Figure 4A), with median CVs of 7.15 (IQR 3.03-11.69) for the raw LTL measurements and 6.53 (IQR 2.87-11.30) for the adjusted LTL measurements. For a larger set of randomly selected but unblinded repeats (n=22,516), the distribution of CVs was similarly skewed (Supplementary Figure 4B) with median CVs of 5.23 (IQR 2.44-6.33) and 5.53 (IQR 2.67-9.68) for the raw and adjusted values respectively.

To quantify within-person variability of LTL values over time, we calculated the regression-dilution ratio (RDR; see Methods) using 1351 available serial measurements of LTL taken at a mean interval of 5.5 years (range: 2-10 years). The RDR for LTL was 0.65 (95% CI: 0.61, 0.68) − similar to that for log_e-transformed LTL (0.68, 95% CI: 0.64, 0.72) − and did not change materially with increasing time between serial measurements or after adjustment for participants’ age at sample collection (Supplementary Figures 5A & 5B). The well-known correlations of LTL with age, sex and other factors among participants with serial LTL measurements were similar to those in the entire UKB cohort (below and Supplementary Figure 6).

Relationship between LTL and selected phenotypes

For these analyses, we focused on participants with LTL measurements on samples collected at UKB’s baseline examination, to match the time when the selected phenotypes were assessed (Figure 1). We also removed individuals where self-reported sex and genetic sex did not match, leaving 472,174 participants for these analyses. Characteristics of these participants, stratified by quartile of LTL values, are shown in Table 2.

Measurement of LTL

Technicians at UKB extracted DNA from peripheral blood leukocytes as part of a cohort-wide array genotyping project, described in detail elsewhere⁴⁰. DNA was extracted using an automated process for the majority of samples; a small proportion were extracted using a manual method using the same chemistry. UKB transported residual DNA from this project to the University of Leicester LTL assay laboratory in 11 tranches of approximately 50,000 samples. Sample manifests including sample ID and concentration were provided alongside the samples. Prior to assay, samples were first normalised to a concentration of 10ng/ul using automated pipetting robots (Qiagility, Qiagen). Research staff at the University of Leicester conducted LTL measurements blinded to phenotypic information.

Using the multiplex qPCR methodology LTL is measured as the ratio of telomere repeat copy number (T) relative to that of a single copy gene (S, Hgb)⁴¹. The amounts of both T and S were measured within each reaction and were calculated relative to a calibrator sample (pooled DNA from 20 individuals) which was included on every run. Each measurement run was set up on a 100 well Rotor-Disc (Qiagen) using an automated pipetting robot (Qiagility, Qiagen) and included 47 samples in duplicate, a no template control and the calibrator sample in quadruplicate. Each qPCR reaction contained 1x Sensimix SYBR No-ROX enzyme mix (Bioline), 150nM Tel primers, 45nM of Hgb primers (Supplementary Table 2) and 30ng of DNA. The Rotor-Discs were transferred to a Rotor-Gene Q PCR machine for amplification. Cycling conditions for each run were as follows: 95°C 10 min; 95°C for 15 sec, 49°C for 15 sec for 2 cycles; 94°C for 15 sec, 62°C for 10 sec, 72°C for 15 sec with signal acquisition (T), 84°C for 10 sec, 88°C for 10 sec with signal acquisition (S) for 32 cycles. At the end of cycling a dissociation curve was included. Prior to use, each primer batch was assessed for quality by producing a standard curve across the input DNA range of 1200-9.3ng in two-fold dilution (8 points). Primers achieving 90-110% reaction efficiency and an R² across the linear range >0.99 were acceptable. Further testing was then performed to reproduce measurements for previously assayed samples with good concordance before further use. The linear range for each primer batch was recorded as a QC metric.

Relative quantities of T and S were calculated for each sample using the Rotor-Gene comparative quantification software (Qiagen). This software calculates the amplification efficiency of each reaction. The relative amount of T and S is calculated using the following equation: Using the calculated average amplification efficiency, rather than assuming 100% efficiency, effectively adjusts the measurements for run-to-run variation. The resulting T/S ratios were calculated for each well, alongside the average T/S and the coefficient of variation for the sample duplicate. We then applied strict, pre-defined QC criteria at both the sample and run levels, as detailed in Supplementary Table 3, before accepting the measurements as being valid. Following this, successful data from each run was uploaded into a custom database. All samples that failed QC criteria were re-assayed until valid measurements were achieved, or the sample was deemed to be unsatisfactory or exhausted.

To measure stability and reproducibility of the measurements subsets of samples were deliberately re-run at later dates and the coefficient of variation between the measurements calculated. For this subsets of samples were selected each week and re-measured. These samples were deliberately selected from early tranches so that as the project progressed reproducibility could be assessed over longer time periods. In addition to these deliberate repeats (n=22,516), a small number of duplicate samples (n=528) were included by UKB, spread across the tranches, to which we were initially blinded (blinded duplicates).

Due to the scale of the project, the samples were measured over a 47 month period by 6 members of staff (“operators”), using 5 Qiagility pipetting robots for liquid dispensing and 8 Rotor-Gene PCR machines (Supplementary Figure 11). It was necessary to use 19 batches of Sensimix SYBR No-ROX enzyme mix and 7 primer batches for the assays (Supplementary Figure 12). Details of these parameters, alongside temperature and humidity (for potential influences on Rotor-Gene and Qiagility performance), were recorded alongside the sample data.

Statistical adjustment of data to minimise technical variation

Adjustment for T/S experimental/technical variation was performed in three stages using R v3.6.1. First, backwards selection using the mean T/S ratios at the run level was used in a linear regression adjusting for enzyme, primer batch, PCR machine, pipetting robot, operator, temperature, humidity, time of day, and extraction method. Only runs with at least 20 valid measurements were included. Significant effects were determined using the Bayesian information criterion. The second stage took all significant main effects identified in stage 1 and further tested all possible two-way interactions using the same backwards selection approach as stage 1 for the interaction effects. For both stages we estimate a partial R² as the difference between the full model R² and the model R² leaving a single parameter out. Individual-level T/S ratios were then partially adjusted based on the coefficients from the final model selected in stage 2. A further level of adjustment was then applied by fitting a linear regression model on the individual level data adjusting for the 260/280 ratio of the DNA sample (stage 3). Due to an observed non-linear relationship between the T/S and 260/280 ratios both linear and quadratic effects were included. For the purpose of this analysis samples with a missing 260/280 or those that had a measurement within the extremes of the distribution (<1 or >3) were imputed using the mean 260/280 value.

After technical adjustments were applied the LTL measurements (T/S ratios) were log_e-transformed due to non-normality (log_e-LTL). To allow direct comparison of the results of our analyses with previous studies we Z-standardised the log_e-LTL measures.

Estimation of regression dilution bias

DNA was extracted by UKB for 1884 participants from a second blood sample taken between 2 and 10 years after the original sample, using the same methodology. To remove technical variation between the two measures for estimation of the regression-dilution the original baseline sample was re-plated alongside the second time point sample and 23 pairs of samples were assayed in each qPCR run. As these DNA samples were received towards the end of the project, for many there was insufficient DNA remaining from the baseline sample (which had already undergone measurement) to allow measurements for both of the paired DNAs to be obtained. Quality control parameters were then applied as for the main dataset. Only samples with valid data for both time points within the same run were taken forward for analysis (Supplementary Figure 13).

We estimated the LTL regression dilution ratio (RDR) coefficient by regressing LTL measured at the second time point on LTL measured at the first time point²⁷. The RDR is the ratio of the between-individual variance to the total variance (i.e. between-individual variance + within-individual variance); RDR values close to 1 indicate little within-individual variability, whereas values close to 0 imply high levels of within-individual variability. The resulting regression coefficient is the RDR, and the multiplicative regression dilution bias (RDB) correction factor, λ, is simply the inverse of the RDR coefficient i.e. Where w_i1 and w_i2 are the first and second measurements of LTL respectively for each of the 1,351 participants.

We further adjusted for the difference in ages between the two measurements to consider the impact of time between sample collections on the RDR estimate and after removing the age effect from the first and second measurements by taking the residuals from a linear regression on LTL adjusted for age. We then regressed the age-adjusted second measurement residuals on the age-adjusted first measurement residuals adjusting for baseline age, sex and difference in age between sample collections to estimate the RDR. For non-LTL traits in UKB shown in Supplementary Table 1, we used baseline and follow-up visit 1 data and ran the models in the same way to estimate the RDR.

Association of LTL with selected phenotypes in UKB

Before conducting analyses we first removed participants for whom the LTL measurement was made from a non-baseline sample (where baseline visit date was before sample collection date) or where self-reported sex and genetic sex did not match (reflecting potential sample mishandling)²⁹. To assess population demographics we estimated means and standard deviations for continuous traits and percentages for categorical traits. To account for familial correlation we randomly excluded one participant from each related pair, where a pair of participants were related if their kinship coefficient was K>0.088 estimated using genetic relatedness. We used linear regression models to assess the association of TL with age, sex, parental age at birth, ethnicity and white blood cell traits. Interactions and non-linear effects were considered in the regression model where appropriate. We consider P<0.05 as the threshold for nominal statistical significance.

Age and sex relationships were assessed first to identify interactions and non-linear effects in the data to estimate population attrition rates. To further investigate the observed age and sex trends we investigated the role of menopause by matching a male to each female 1:1 on age at baseline running stratified analyses by pre- and post-menopause status.

We calculated parental age at birth from the reported parental age at baseline minus the age of the participant at baseline. We first modelled parental age at birth adjusting for age and sex and then calculated the difference in paternal and maternal age running analyses stratified by age difference group, 2-5 years and >5 years and run separately. Similarly, for ethnicity, regression models were stratified by ethnic group and run separately to assess the age and sex attrition rates within each ethnic group. We used the UKB defined ethnic groups from self-reported data (Data-Field 21000). Both “British and Black British” and “Asian and British Asian” are shortened to “Black” and “Asian” throughout. The “Asian and British Asian” is largely comprised of South and West Asian ancestries. We considered collinearity in these models through estimation of the variance inflation factor (VIF) where a value > 5 is considered to indicate collinearity.

Finally, we fit a multivariable model to assess the contribution of white blood cell traits. All white blood cell traits were winsorized at the 0.5% and 99.5% centile to reduce the impact of extreme values, log-transformed if required and Z-standardised. Linear regression models were again used to quantify the association with total white blood cell count on TL. We also included white blood cell composition in the model with the percentages of neutrophils, monocytes, eosinophils, lymphocytes and basophils. All phenotype analyses were run using Stata v16.0.