The Balancing Role of Distribution Speed against Varying Efficacy Levels of COVID-19 Vaccines under Variants

Introduction

Since the initial reports of a cluster of pneumonia cases of unidentified origin in Wuhan, China, in December 2019, more than 133 million people around the world have been infected with the novel severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). Despite the development of effective vaccines in unprecedented speed, concerns have been raised on the potential reduction in efficacy of these vaccines against the new SARS-CoV-2 variants due to possible evasion from antibody recognition [1]. Most of the vaccines were developed and tested before the new variants of SARS-CoV-2 emerged. In order to reach herd immunity, effective implementation of a vaccine with sufficient efficacy against the circulating dominant variants is essential. Subsequently, it becomes a trivial decision for policymakers and governments to favor a vaccine with high efficacy for distribution. However, if the vaccine cannot be dispensed quickly and/or if its efficacy drops significantly against the emerging variants compared to other vaccines, the question of which vaccine should be favored is no longer trivial. Hence, the goal of this study is to understand the tradeoffs between the speed of distribution vs. the change in the efficacy levels of SARS-CoV-2 vaccines before and after the emergence of variants, which we refer to as “initial efficacy” and “final efficacy”, respectively, hereafter.

As of March 2021, twelve vaccines have received authorizations for emergency use around the world [2]. Pfizer-BioNTech’s mRNA vaccine, which was the first authorized vaccine in the United States, has an initial efficacy of 95% and needs to be stored at about minus 70 degrees Celsius [3, 4]. Moderna’s mRNA vaccine has an initial efficacy of 94.5% and needs to be stored at about minus 25 degrees Celsius [5]. Both mRNA vaccines require two doses with three to four weeks apart application. Johnson & Johnson’s adenovirus-vectored vaccine has an average initial efficacy of 66.3%, requires only a single dose, and needs to be stored at about 2-8 degrees Celsius [6]. Even though there are multiple authorized vaccines, their distribution and administration have been slow. By the end of 2020, only 2.8 million people received the first dose of COVID-19 mRNA vaccines in the United States [7]. Moreover, the Centers for Disease Control and Prevention (CDC) reports that only about 10% of the population have been fully vaccinated as of March 11, 2021 [8].

In addition to distributional challenges, reduction in efficacy of vaccines against emerging variants has raised concerns. As of March 2021, three main SARS-CoV-2 variants have been identified. The B.1.1.7 variant, first identified in the United Kingdom in September 2020, caused more than 28% of the infected cases in the United Kingdom in late December 2020, spread 56% more quickly than other variants, and has become dominant in the United States [9, 10]. Another variant B.1.351, first identified in South Africa in December 2020, has become dominant, making up to 90% of infections, in South Africa and has been detected in several countries. The last variant P.1 has been identified in Japan from travelers from Brazil in January 2021. In response, scientists and vaccine manufactures have been testing the efficacy of the vaccines against the variants and report that the B.1.1.7 variant is neutralized by most of the vaccines, supporting the retention of the efficacy [11]. However, in vitro studies show that the vaccines’ neutralization of B.1.351 variant is significantly lower than that of other variants [12, 13]. In particular, the distribution of AstraZeneca’s adenovirus-vectored vaccine in South Africa has been halted due to its low efficacy against the B.1.351 variant. Similarly, Novavax states that its protein-based vaccine is 85.6% effective against the B.1.1.7 variant but 60% effective against the B.1.351 variant [14].

In this paper, we study the trade-offs between vaccines’ efficacy levels, which are subject to reduction due to emerging variants and speed of vaccine distribution by using a modified Susceptible-Infected-Recovered-Deceased (SIR-D) model and simulating the infection attack rate (IAR) under different times that the virus variants emerge. Throughout this paper, we refer to vaccine distribution as the entire distribution process of a vaccine including delivery to the dispensation sites and administration to the population. The results of this study are aimed to guide decision-makers in vaccine ordering during a pandemic when there are multiple types of vaccines, facing reduced efficacies as variants emerge.

Methods

To compare different vaccine types, we categorized the level of the vaccine efficacy into three ranges: “H” (High) if 90% or above, M (Moderate) if higher than 70% and lower than 90%, and L (Low) if lower than 70%. We assumed that the final efficacy was always lower than the initial efficacy. In our main simulation, we considered three initial efficacy levels (H_i = 95%,M_i = 75%, and L_i = 65%) and three final efficacy levels (H_f = 90%, M_f =70%, and L_f = 60%). Consequently, we obtained six types of vaccines, defined by a particular initial and final efficacy, as summarized in Table 1. These modeling choices were motivated by recent studies on vaccine efficacy against variants. The recently updated analysis of Pfizer-BioNTech’s phase 3 clinical trials showed that their vaccine is effective against the B.1.351 variant [15]. The clinical trials of Johnson & Johnson’s adenovirus-vectored vaccine showed an efficacy of 57% in South Africa, where the B.1.351 variant is dominant [16]. Hence, in our model, vaccine-H_iH_f or vaccine-H_iM_f may represent Pfizer-BioNTech’s mRNA vaccine and vaccine-L_i L_f may represent Johnson & Johnson’s adenovirus-vectored vaccine.

Even though all authorized COVID-19 vaccines, except for Johnson & Johnson’s adenovirus-vectored vaccine, require two doses, we assumed in our simulations that all vaccines require a single dose and an individual who receives an effective vaccine becomes immunized immediately. In each simulation, only a single type of vaccine was administered, and the daily vaccine distribution capacity was kept constant at λ · K, where K represents base capacity and λ is a multiplier. We fixed the base capacity, K, at 500,000, motivated from the average number of vaccine recipients in each day in the United States from December 14, 2020 to March 2, 2021, and we set a range of 1.0 to 3.0 with increments of 0.2 for the capacity multiplier λ to represent the speed of distribution in our simulations [8].

In our study, we utilized a modified SIR-D (Susceptible-Infectious-Recovered-Deceased) compartmental model, which is a simplified mathematical model of infectious diseases. In this model, individuals are moving among compartments, and transitions between compartments are governed by ordinary differential equations given epidemiological and vaccine parameters. We implemented seven compartments: Susceptible, Immunized, Vaccinated-susceptible, Symptomatic-infectious, Asymptomatic-infectious, Recovered, and Deceased. When Susceptible population receives vaccines, they enter either the Immunized compartment if the vaccine is effective, or the Vaccinated-susceptible compartment, otherwise. Both Susceptible and Vaccinated-susceptible populations enter either the Symptomatic-infectious or Asymptomatic-infectious compartment, depending on whether they show symptoms or not, once they make infectious contacts with the infected population. Symptomatic-infectious population moves to either the Recovered or Deceased compartment. Asymptomatic-infectious population, on the other hand, moves only to the Recovered compartment.

We chose the epidemiological parameter values that govern the transitions in the compartment model based on the estimated SARS-CoV-2 characteristics in various studies. You et al. (2020) and Byrne et al. (2020) reported that the infectious period of a symptomatic patient and an asymptomatic patient was around 14 days and 8 days, respectively [17, 18]. Therefore, we set the recovery rates of symptomatic patients (γ_s) and asymptomatic patients (γ_a) at 1/14 and 1/8, respectively. In addition, the CDC has developed COVID-19 Pandemic Planning Scenarios and provided parameter values to use in a mathematical model [19]. Accordingly, we assumed that 60% of the susceptible population who make infectious contacts become symptomatic. In addition, we used 2.3 for the reproduction number, which is often employed by epidemiologists to represent the severity of a disease. Even though the CDC’s planning scenarios, lastly updated in September 2020, specify a reproduction number of 2.5 as the best planning estimate, we expect a lower reproduction number due to an increase in mask use and the implementation of various non-pharmaceutical interventions [20]. Basu (2020) reported that the symptomatic infection fatality rate (IFR-S) of COVID-19, the proportion of deaths among symptomatic infected individuals, was estimated to be 1.3% [21]. Given the reproduction number of 2.3 and the IFR-S, we set the symptomatic-transmission rate (β_s) to be 0.22031 and the death rate (µ) to be 0.0032. We assumed that the asymptomatic-transmission rate (β_a) was 75% of the symptomatic-transmission rate [22]. We used R-software to run the simulations with a population size of 330 million (approximate population of the United States). Since our main goal is to analyze the trade-offs between distribution speed and vaccine’s efficacy under variants, we started the simulation only after when the vaccine becomes available and initialized it such that around 28% of the population had already been infected. Thus, we set 2.90% of the population as symptomatic-infected, 1.15% as asymptomatic-infected, 24.44% as recovered, and 0.14% as deceased. These estimates were motivated by the confirmed cumulative cases and deaths as of December 14, 2020, the first day of vaccine distribution in the United States [23]. However, we multiplied the number of confirmed infections by six and increased the number of confirmed deaths by 35% in line with the findings of Wu et al. (2020) and Noh and Danuser (2021), who reported that the number of COVID-19 confirmed cumulative cases was underestimated, and Kung et al. (2020), who showed the same for confirmed deaths [24-26]. The initial values in other compartments were estimated using the epidemiological parameters defined previously. We ran the simulation on a one-year planning horizon under different mutation times (i.e., the time at which the emerging variants cause a decrease in a vaccine’s efficacy) within the range of day 5 to day 40 with a discrete step size of 5 days, and different capacity multipliers (λ) within the range of 1.0 to 3.0 with a discrete step size of 0.2 to capture the vaccine distribution speed. We evaluated the impact of each vaccine type using IAR as the main health outcome.

Results

We first ran our simulation without the presence of any vaccines, which gave an estimated IAR of approximately 81% and IFR-S of 2%. The daily infection peak (i.e., the highest percentage of the population who get newly infected on a single day) occurred on day 24, at which 1% of the population got newly infected.

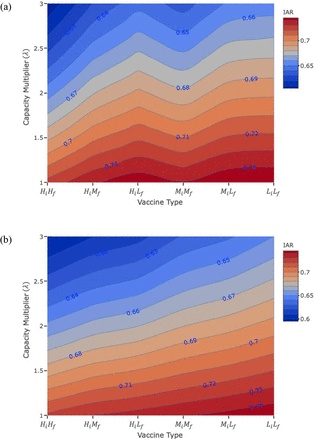
Table 2 shows the estimated IAR under different capacity multipliers (λ) when the mutation times are day 5 and day 25. We report additional results with different mutation times in Supplemental Materials. When the mutation time is day 5, the level of IAR is between 60% and 65% when the capacity multiplier is 3.0 (1.5M doses/day) and between 72% and 75% when the capacity multiplier is 1.0 (0.5M doses/day), depending on the selected vaccine type. When the mutation time is day 25, the level of IAR is smaller compared to when the mutation time is day 5, and the decrease in IAR due to the increase in capacity multiplier is larger.

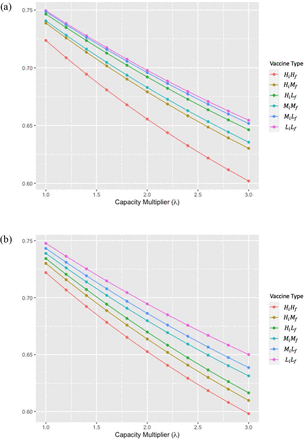
Figure 1 and Figure 2 present the contour plot and the two-dimensional plot of the IAR in Table 2, respectively. Figure 1 shows that even vaccine-L_iL_f can achieve a lower IAR than vaccine-H_iH_f if the capacity multiplier of vaccine-L_iL_f is high compared to that of vaccine-H_iH_f For instance, when the capacity multiplier of vaccine-H_iH_f is 1.0 and the mutation time is day 5, 72.3% of the population is infected. However, if the capacity multiplier of vaccine-L_iL_f is 1.48 (or higher), 72.2% (or less) of the population is infected. We present the minimum required capacity multiplier of all vaccine types to achieve a lower IAR than vaccine-H_iH_f with the capacity multiplier of 1.0 and 1.6 under different mutation times in Supplemental Materials.

• Download figure
• Open in new tab

Figure 1:

Contour plot of infection attack rate under different capacity multipliers with different vaccine types when mutation time is (a) day 5 and (b) day 25

• Download figure
• Open in new tab

Figure 2:

Two-dimensional plot of infection attack rate under different capacity multipliers with different vaccine types when mutation time is (a) day 5 and (b) day 25

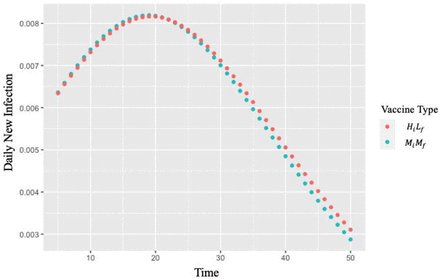
Figure 3 compares the daily new infections from day 5 to day 50 with vaccine-H_iL_f. vaccine-M_iM_f. In this figure, the mutation time is early (on day 5) and comes before the daily infection peak, and thus, vaccine-M_iM_f results in a better IAR than vaccine-H_iL_f for all capacity multipliers. Specifically, after the peak of daily new infections is reached for each vaccine, the number of daily infections drops at a faster rate when vaccine-M_iM_f is administered. On the other hand, when the mutation time comes after the daily infection peak (not shown in the figure), vaccine-H_iL_f achieves a lower IAR than vaccine-M_iM_f for all capacity multipliers.

• Download figure
• Open in new tab

Figure 3:

Daily new infections from day 5 to day 50 with vaccine- and vaccine-when the capacity multiplier (is 3 and the mutation time is day 5

Discussion

In this study, we utilized a modified SIR-D model to simulate the trajectory of an infectious disease under the intervention of different kinds of vaccines of which efficacies decrease against the variants of the disease. We have demonstrated that the speed of the vaccine distribution is a key factor to achieve low IAR levels, even though the vaccine may have high efficacy both before and after the variants emerge. There have been many studies examining the trade-offs between speed and efficacy [27, 28]. These studies emphasize the importance of wide vaccination coverage, which is consistent with our study’s findings. However, we considered a decrease in efficacy of each vaccine type in the midst of the pandemic and reaffirmed the importance of a rapid implementation of vaccination even under emerging variants.

Our study shows that a vaccine with low initial and final efficacy levels (vaccine-) can achieve a lower IAR than a vaccine with high initial and final efficacy levels (vaccine-) if the former can be distributed more quickly than the latter, regardless of the mutation time. For instance, when the mutation time was day 25 and the capacity multiplier of vaccine-H_iH_f was 1.0 (0.5M doses/day), 72.2% of the population got infected. If the capacity multiplier of vaccine-L_iL_f was 1.47 (0.73M doses/day or higher), 72.1% (or less) of the population was infected. Even for vaccines with the same initial efficacy, such as vaccine-H_iH_f and vaccine-H_iL_f, this result remained robust—vaccine-H_iL_f with a capacity multiplier of 1.18 (0.59M doses/day) or higher achieved a lower IAR than vaccine-H_iH_f with a capacity multiplier of 1.0 (0.5M doses/day). Since the start of the COVID-19 vaccination process, the speed of the vaccine distribution has been slow due to numerous reasons, including limited and uncertain vaccine supply and various logistics and storage challenges. Despite the continuing effort of increasing production capacities, vaccine manufacturers, especially those who produce mRNA vaccines with new technology, have been struggling to secure sufficient supply of vaccine ingredients, storage containers, and more, due to the demand from billions of people around the world [29]. In addition, mRNA vaccines need to be stored in ultra-cold freezers under specific expiration dates, although many facilities lack or cannot afford such expensive ultra-cold freezers, leading to a limited number of administration sites. Even the sites with the ability to administer these vaccine types need to dispose the vaccines if they cannot be administered by the expiration date or stored at the appropriate temperature [30, 31]. Unlike the mRNA vaccines, Johnson & Johnson’s adenovirus-vectored vaccine only requires a single dose and can be stored at the same temperature as the seasonal flu vaccine. These characteristics prevent vaccine wastage, enable efficient production and distribution using the existing vaccine supply chain, and facilitate a faster rate of vaccination [32]. Hence, despite the lower efficacy, adenovirus-vectored vaccines that have the potential for faster distribution may be more beneficial.

Increasing the doses distributed per day, i.e., the capacity multiplier (λ), of any vaccine type is always beneficial as it reduces the size of the susceptible population and can, eventually, achieve herd immunity. Our study showed that the level of IAR always decreased when the capacity multiplier was higher, with the largest impact observed for vaccine-H_iH_f. In particular, when we compared the impact of changing the capacity multiplier from 1.0 to 3.0 for vaccine-H_iH_f, vaccine-M_iM_f, and vaccine-L_iL_f, IAR changed from 72.20% to 59.81% for H_iH_f, from 73.89% to 63.13% for M_iM_f, and from 74.77% to 65.01% for L_iL_f, when the difference between the initial and final efficacy was 5% for all the vaccine types and the mutation time was day 25. In addition, if vaccine-H_iH_f could be distributed at a faster rate, the minimum required capacity multiplier (λ) of vaccine-L_iL_f to achieve a lower IAR than vaccine-H_iH_f was even larger. For example, when the mutation time was day 25, the capacity multiplier of vaccine-L_iL_f needed to be at least 1.47 to achieve a lower IAR than vaccine-H_iH_f with the capacity multiplier of 1.0. On the other hand, when the vaccine-H_iH_f ‘s capacity multiplier was 1.6, the capacity multiplier of vaccine-L_iL_f needed to be at least 2.35. Thus, even though the difference in the capacity multiplier of vaccine-H_iH_f was only 0.60, that of vaccine-L_iL_f was 0.88. However, increasing the capacity multiplier, i.e., the speed of distribution, for vaccine-H_iH_f, which represents mRNA vaccines in our model, may be much more challenging than that for vaccine-L_iL_f, as described above, including economic burden, complications in vaccination programs, and unsophisticated infrastructure. In such cases, it may be more beneficial to allocate resources towards distributing a lower efficacy vaccine at a faster rate as our study shows.

Forecasting the daily infection peak and the mutation time also plays an important role when choosing which type of vaccine to distribute. If the mutation time comes after the daily infection peak, a vaccine with a higher initial efficacy always achieves a lower IAR than a vaccine with lower initial efficacy. However, if the mutation time comes before the daily infection peak, the final efficacy level determines which vaccine type achieves a lower IAR under the same capacity multiplier. For example, when we compared vaccine-H_iH_f and vaccine-M_iM_f with a capacity multiplier of 1.0 for each, the daily infection peak occurred on day 22 for both vaccines. Then, the administration of vaccine-M_iM_f, which has an initial efficacy of 75% and final efficacy of 70%, resulted in an IAR of 74.06%, whereas the administration of vaccine-H_iL_f, which has an initial efficacy of 95% and final efficacy of 60%, resulted in an IAR of 74.65%. This is because an effective vaccination program achieves the highest reduction in the number of new infections before the daily infection peak. Afterwards, even with a higher initial efficacy, a vaccine with a lower final efficacy cannot reduce the size of the susceptible population as much as a vaccine with a lower initial efficacy and a higher final efficacy. Different variants of SARS-CoV-2 that reduces the efficacy of the authorized vaccines have been identified and their potentially higher transmissibility may cause future waves of infections. Thus, careful in vitro and clinical trials against variants are essential before making decisions on vaccine ordering.

We acknowledge some limitations of this study. First, our SIR-D model did not capture the full trajectory of SARS-CoV-2. Tindale et al. (2020) reported that the transmission of SARS-CoV-2 starts prior to symptom onset and Cevik et al. (2020) reported that the COVID-19 is most contagious in the first five days of illness, which we did not incorporate into our model [33, 34]. In addition, we assumed that the population gains immunity as soon as they receive effective vaccines and that every type of vaccine requires a single dose. In practice, all the authorized vaccines, except Johnson & Johnson’s adenovirus-vectored vaccine, require two doses with three to four weeks apart application and it may take several days to gain immunity after vaccination. Moreover, we did not consider any type of non-pharmaceutical interventions. Depending on the number of people who conform to the interventions, such as social distancing and mask mandates, the probability of infectious contacts may vary over time. Lastly, variants may be more transmissible, but we assumed a constant transmission rate in each simulation.

Overall, our results suggest that the administration of a vaccine with high efficacy against both the original strain and the variants may not always lead to a low number of cumulative infections if it cannot be distributed as quickly as other vaccine types with lower efficacies. Despite the vast efforts for worldwide vaccination, the vaccine distribution has been an ongoing challenge due to production shortages, economic constraints and the lack of ultra-cold-chain infrastructure, which is critical to distribute some of the early-authorized vaccines. Due to these challenges, especially many low- and middle-income countries have not received a single dose of a vaccine as of mid-February, 2021 [35, 36]. It is critical to distribute available vaccines as quickly as possible and vaccinate more people to reach herd immunity before new variants spread. Our study demonstrates that a vaccine with a relatively lower efficacy can achieve at least as good health outcomes as their higher efficacy counterparts, as long as it can be distributed more quickly. We hope that our study provides guidance to decision makers on the tradeoffs between speed and efficacy, highlighting the critical role of speed of vaccination during a pandemic as variants that decrease efficacy of vaccines emerge.