Altered resting-state functional connectivity in hiPSC-derived neuronal networks from schizophrenia patients

Differentiation of NSC to mature neuronal cultures

hiPSC-derived NSC from 3 healthy subjects and 4 SZ patients were kindly donated by Dr. Stevens Rehen at D’Or Insitute and Feredal Univeristy of Rio de Janeiro. Differentiation of hiPSC to NSC was performed as previously published [23]. The establishment of hiPSC, and derivation of NSC lines were carried out in accordance with international standards and with the approval of the Research Ethics Council “Comité de Ética em Pesquisa – Hospital Copa D’Or, Rua Figueiredo Magalhães 875, Rio de Janeiro, Brasil.” (Certificado de Apresentação de Apreciação Ética (CAAE): 32385314.9.0000.5249). Detailed information on patient samples and reprogramming protocol can be found in Table S1. NSC differentiation to mature neuronal networks was conducted adapting a protocol of Shi et al. [24]. NSCs were thawed and seeded in Geltrex-coated plastic 60 mm plates and maintained in Neural Expansion Media (NEM; DMEM/F12 and Neurobasal medium (1:1) with Neural Induction Supplement; Thermo Fisher Scientific, Carlsbad, CA, USA) until they reached 80-100% confluence. Next, NSC were detached from the plate with accutase (7 min/37ºC), centrifugated at 300g for 4 min, and resuspended in NEM plus 10 µM Rock Inhibitor (Y-27632; Merck, Darmstadt, Germany). 1*10^6 cells were plated in 35 mm petri dishes coated by poly-l-ornithine/laminin (10 μg/ml and 2.5 μg/ml respectively). After 48 h, the medium was replaced by Neural Differentiation Media (NDM; DMEM/F12 and Neurobasal medium (1:1) supplemented with 1×N2, 1×B27, 2-Mercaptoethanol 100uM). NDM was changed every two days. 14-16 days after plating, cells were detached from the plate with accutase and passed in a 1:3 ratio into 35 mm poly-l-ornithine/laminin-coated plates. Medium changes were done every 2 days. Around day 30, cells were passed into their final coated 35mm plate, in a 1:4 ratio (around 500.000 cells per 35 mm petri dish). Cells were maintained in NDM, with medium changes every other day, for 60 more days and were supplemented with 10 µM Rock inhibitor for 48 h, after every passage.

Immunofluorescence

At 60 days of differentiation, cells were fixed with paraformaldehyde 4%, permeated with Triton-X (Sigma, St. Louis, MO, USA) 0.2%, blocked with BSA 5% in PBST (tween-20 0.1% in PBS) solution, and incubated overnight at 4ºC with anti-tau1 (mouse; #MAB3420 Milipore), anti-synaptophysin (mouse; #101011 Synaptic Systems), anti-MAP2 (rabbit; #AB5622 Millipore), anti-homer-1 (rabbit; #160002 Synaptic Systems). Subsequently, cells were incubated with secondary antibodies (goat anti-mouse alexa 488, goat anti-rabbit alexa 555, Invitrogen). Nuclei were stained with 4′-6-diamino-2-phenylindole (DAPI) 1µg/mL for 5 min. Images were acquired with a Zeiss LSM 710 bi-photonic confocal microscope.

Electrophysiology

Whole-cell voltage-clamp recordings were performed at 60 days of differentiation in HC and SZ-derived cultures. Neurons were selected following morphological criteria. Na⁺ inward and K⁺ outward currents were evoked by voltage steps ranging from -100 to +40 mV in 10 mV increments (V_hold = -75 mV). Data was acquired at 50 kHz and low-pass filtered at 2.9 kHz, by an EPC-10 amplifier (HEKA Elektronik GmbH, Reutlingen, Germany). Patch electrodes (∼4.5 MΩ) were pulled from borosilicate glass and the intracellular solution contained (in mM): 135 K-gluconate, 2 MgCl₂, 2 Na₂ATP, 0.3 NaGTP, 10 HEPES, 7 NaCl (pH 7.4). The recording chamber was continuously perfused at 1–2 ml/min with ACSF solution containing (in mM): 115 NaCl, 2.5 KCl, 1.3 NaH₂PO4, 26 NaHCO₃, 25 glucose, 5 Na-Pyruvate, 2 CaCl₂ and 1 MgCl₂ (300 mOsm/kg), gassed with 5% CO₂/95% O₂ (pH 7.4). Recordings were performed at room temperature (20–25 °C). Series resistance (10–40 MΩ) was not compensated and recordings were discarded for variations higher than 20% along the experiment.

qPCR

RNA was obtained from early differentiated cells (30 days) or late differentiated cells (range of 70-91 days, herein defined as 90 days) and stored in Trizol (Thermo Fisher Scientific, Carlsbad, CA, USA) at - 80ºC until further use. For each line donor, three SZ (#1,3-4) and three HC (#1-3) samples from independent differentiation procedures were pooled at each time frame to extract total RNA. cDNA was synthesized from 1 μg RNA, using a M-MLV reverse-transcription kit (Promega, Madison, WI, USA). Primers were specifically designed to measure expression of the genes listed in Figure S1A. Relative gene expression was assessed by qPCR (Agilent Technologies Thermocycler, Santa Clara, CA, USA). mRNA levels were calculated as the fold-change expression via 2^-ΔΔCt and gene expression was normalized to three different housekeeping genes (B2M, 18S, GAPDH). Fold-changes were assessed relative to control sample or differentiation time.

Conditioned medium (CM) collection and neuro-proteomic profile

The presence of 30 different neuronal growth factors in serum-free 48 h collected CM (four SZ (#1-4) and three HC (#1-3)) was evaluated from 75 days cell cultures using the Human Neuro Antibody Array II (#ab211063, Abcam, Cambridge, UK). Spots were detected by chemo-luminescence and intensity quantified by densitometry (ImageJ, NIH, USA). The levels of each factor were measured in duplicate and normalized to internal controls provided by the assay.

Statistical Analysis for mRNA expression and neuro-proteomic profile comparisons

mRNA fold-change normality was assessed with D’Agostino-Pearson and significance of mRNA was determined by a Nested t-test. A linear mixed model with a random intercept for cell-line id was performed to test between- and within-group differences in secreted proteins measured with the neuro-proteome array. Significance of the regression coefficients associated to the group, we used a Z test and Bonferroni correction for multiple comparisons. Statistical significance was set at p < 0.05.

Calcium imaging

Ca²⁺ transients were recorded at a single-cell resolution at up to 90 days (range of 80-90 days) of differentiation. Three SZ (#2, 3 and 4) and two HC (#1 and 2) cell lines were analyzed (2-3 plates per cell line; 3-27 networks per plate). We used the cell-permeant Ca²⁺ indicator Oregon Green™ 488 BAPTA-1 (OGB-1 AM), (Thermo Fisher Scientific, Carlsbad, CA, USA). The loading solution consisted of OGB1 3.2 µM, Cremophor EL (Merck, Darmstadt, Germany) 0.01% v/v and Pluronic F-127 (Merck, Darmstadt, Germany) 0.4% in NDM. Cells were incubated at 37°C and 7% CO₂ in the dark for 1 h. After washing twice with NDM, cells were maintained for 30 min before imaging in ACSF (∼ 4.7 min at 10 Hz). In some experiments, TTX (0.2 µM) was added to the bath solution to confirm the AP-dependence of Ca²⁺ transients.

Imaging analysis

Molecular profiling of long-term hiPSC-derived neuronal cultures from SZ and HC subjects

Given the relative scarcity of studies on functional maturation in long-term hiPSC-derived neuronal cultures over time, we first aimed to validate and characterize the differentiation process. We used hiPSC-derived Neural Stem Cell (NSC) cultures from HC and SZ patients, displaying clear staining for NESTIN and PAX6, the two most well-known markers for NSC [23]. We modified the protocol from Shi et al., 2012 [24] to induce long-term neuronal differentiation from four SZ and three HC NSC lines (see Table S1 for details). We omitted the use of antibiotics, as they may affect neuronal excitability [28] and modify the expression of several of genes [29]. HC and SZ patient-derived hiPSC aggregated and formed neuronal rosettes that became larger and more defined along the differentiation process [21]. After 30 days, 3D neuronal aggregates were already easily identified (Figure 1A-D). At 60 days, neurons expressed specific dendritic and axonal markers (MAP2 and TAU, respectively); MAP2 was expressed in perikarya and dendrites (Figure 1E, G), while TAU was mainly found in axons (Figure 1F, H). The pre and postsynaptic proteins synaptophysin (SYP) (Figure 1E, G) and HOMER1 (Figure 1F, H), respectively, were also detected, confirming the presence of synaptic structures. Moreover, both HC and SZ hiPSC-derived neurons displayed voltage-dependent Na⁺ and K⁺ currents (Figure 1I, J).

• Download figure
• Open in new tab

Figure 1. Profiling of hiPSC derived neurons obtained from HC and SZ patients.

(A-D) Representative images for HC (A, C) and SZ (B, D) derived neuronal cultures, captured with phase-contrast microscopy at 30 (A, C) and 90 (B, D) days of differentiation. Arrows indicate 3D neuronal aggregates where spontaneous activity was recorded. Calibration bar: 200µm. (E-H) Representative immune staining for the dendritic and axonal markers MAP2 (E, G) and TAU (F, H), respectively, as well as for the pan-presynaptic and glutamatergic-postsynaptic proteins synaptophysin (SYP) (E, G) and HOMER1 (F, H), respectively. DAPI staining is shown in blue. Calibration bar: 36 µm. (I, J) Representative voltage-clamp electrophysiological recordings at 60 days of differentiation, for HC and SZ-derived neurons. (K) Quantification of neurogenic protein levels (mean ± SD) in the CM of four SZ (#1-4) and three HC (#1-3) cell lines at 75 days of differentiation. (L-U) Fold-change in mRNA expression levels of different genes related to central nervous system development, in the period from 30 to 90 days. Data is presented as the log2 of the 90/30 days ratio for three SZ (#1, 2, and 3) and two HC (#2 and 3) cell lines. B2M was used as housekeeping; *p <0.05, nested t-test.

The functional competence of our differentiated cell cultures was further assessed by analyzing their secretome. The expression profile of different cytokines/growth factors related to neuronal differentiation and signaling was evaluated by collecting the serum-free CM) from the SZ and HC cell lines (Figure 1K). Quantification of secreted proteins at 75 days of differentiation revealed a similar profile; the complete set of targeted proteins was identified (although Eotaxin-3 and Interleukin-18 were barely detected; Figure S2). Altogether, these results validate the correct establishment of HC and SZ neuronal cultures.

Altered expression of genes involved in synaptic function and network establishment during SZ neurodevelopment

We analyzed the expression of a set of genes reported to be altered in SZ. Gene expression was quantified by qPCR at two different time points during the neurodevelopmental process: 30 and 90 days in culture (Figure S1A). First, we evaluated genes encoding selected synaptic proteins, including the glutamatergic NMDA-receptor subunit 1 GRIN1 and the postsynaptic scaffolding protein HOMER1 [30]; as well as the GABAergic postsynaptic anchoring protein GEPHYRIN [31]. We also assessed the gene coding for the pan-presynaptic vesicle-associated protein synaptophysin SYP. SZ and HC synaptic phenotypes do not display significant disparities for these genes when compared at the same culture age (Figure S1B). To explore how glutamatergic and GABAergic synapses evolve over time in both conditions, we quantified gene expression change between 30 and 90 days in vitro (90/30 days ratio; Figure 1L-O). For details on statistical tests and p-values, see Methods and Materials, Figure 1 and Table S3). Notably, HOMER1 evolution was significantly different among both conditions (Figure 1L); while expression decreased in HC lines, it increased in SZ. A difference among groups was also detected for GRIN1 (Figure 1M), with a significant decrease in HC and a trend to increase in SZ. These results point to a divergent evolution in the number or strength of excitatory synapses during early neurodevelopment. On the other hand, expression of the GABAergic marker GPHN was reduced in both conditions along this period (Figure 1N), suggesting a decline in GABAergic communication over time. However, the reduction was significantly lower in SZ. Differences in SYP expression (Figure 1O) probably reflect the combined effect on excitatory and inhibitory synapses, further supporting an altered evolution of synaptic connectivity over time in SZ compared to HC networks. Overall, these results are consistent with previous hypotheses proposing an altered excitatory/inhibitory balance in SZ brains [32] and suggest that these abnormalities may originate at early stages of neurodevelopment.

We also evaluated expression changes over time of different genes implicated in neurodevelopment, as CDK5R1 and REELIN (RELN). CDK5R1 codes for p35, the neuronal-specific activator of cyclin-dependent kinase 5 (CDK5) regulatory subunit 1 [33]. CDK5 is involved in orienting neuronal network structure and regulating activity during neurodevelopment, via cytoskeleton remodeling [34]. Expression of p35, and hence CDK5 activity, varies cyclically along brain development [35]. During the assessed period, we found a reduction of CDK5R1 expression in both conditions (Figure 1P, Table S3). Nonetheless, this decrement was significantly lower in SZ than in HC cultures (Figure 1P). The extracellular-matrix glycoprotein REELIN plays a critical early role in neuronal migration [36]. Later, it modulates dendritic and axonal outgrow, and spine maturation, by regulating the cytoskeleton. Interestingly, while RELN did not significantly change in HC in the observed period, it decreased in SZ (Figure 1Q, Table S3). Glutamate decarboxylase GAD67 is involved in GABA synthesis, but for neuron properties no directly related to neurotransmission, as synaptogenesis and neuroprotection [37]. In contrast to HC, we detected a significant increase in GAD67 in SZ along the evaluated period (Figure 1R, Table S3).

Since metabolic anomalies have been associated to SZ [38], we also evaluated the expression of ATP5, coding for mitochondrial-membrane ATP synthase. ATP5 expression decreased in the same time interval in HC networks, but did not change in SZ ones (Figure 1S, Table S3). An abnormal energy metabolism during early neurodevelopment might have multiple consequences on network establishment and function [39].

Finally, we did not detect changes in the glucose transporter 1 gene (GLUT1) and the member of the semaphorin family SEMA3A along time (Figure 1T-U).

Calcium imaging in hiPSC-derived neuronal networks

Previous studies have assessed neuronal structural connectivity in hiPSC-derived neurons using trans-neuronal spread of rabies virus [19, 40]. Neuronal cultures derived from SZ patients presented a decrease in transsynaptic tracing [40], which could be due to a decrement in the number of synaptic connections. However, electrophysiological recordings revealed similar spontaneous synaptic activity in SZ and HC cultures [40]. The activity of neurons triggering action potentials can be monitored by sensing changes in intracellular Ca²⁺ concentration [41]. To address neuronal network connectivity from a functional perspective, we recorded the spontaneous activity of hiPSC-derived populations of neurons at a single-cell resolution and quantified the co-variation of activity patterns between each pair of neurons (3-27 networks per plate, 2-3 plates per cell line, 3 SZ and 2 HC cell lines, Table S1).

Cell cultures were loaded with the cell-permeant Ca²⁺ indicator OGB1 (Figure 2A, B). We recorded 4.7 min length videos (10 pictures/second) of different regions of interest (ROI) within the cell plates, while illuminating with blue light (OGB1 peak absorption = 493 nm). Spontaneous activity was found with a higher probability in neuronal aggregates protruding from the base of the plate (Figure 1B, D; black arrow), as previously described [21]. Since each local network had a unique structure, varying in size and shape even within each culture plate, we considered these aggregates as the ROIs to study. All measurements and analyses were conducted in these 3D neuronal aggregates. We identified the active neurons within the ROI using the open-source tool CaImAn software, considering a signal-to-noise ratio above 2.5 [26]. The set of active neurons within an aggregate was defined as a neuronal network. Ca²⁺ transients (ΔF) were quantified from large populations of cells (Figure 2C, D). Action potential-evoked Ca²⁺ transients depended on the activation of voltage-gated Na⁺ channels as their frequency was strongly decreased after adding tetrodotoxin (TTX; 0.2 µM) to the bath during recordings (reduction of about 43% in the number of active neurons, from 240 to 137; Figure S3).

• Download figure
• Open in new tab

Figure 2. Functional connectivity (FC) and topology analysis in HC and SZ networks.

(A, B) Representative ROI images of HC and SZ neuronal cultures loaded with the Ca²⁺ indicator OGB-1. (C, D) Ca²⁺ fluctuations (change in fluorescence intensity relative to baseline (80% of the signal)) in 5 randomly selected neurons from an HC and a SZ network. (E) Static FC matrix displaying the average Pearson’s correlation index (color bar) between Ca²⁺ signals from each pair of neurons in an HC network. (F) Frequency plot of Pearson’s correlation coefficients among neuron pairs from all networks. The dotted red line represents the threshold beyond which we considered a pair of neurons as functionally connected. (G) Probability density of finding a neuron with “x” number of functional connections (connectivity degree). The connectivity distribution does not fit to a Poisson (λ = 8) nor to a Binomial (n = 1000, p = 0.008) distribution. (H) Plot of the connectivity-degree logarithm (log10) versus the probability logarithm. Data fits a scale-free or long-tailed distribution, with a scaling exponent of -1.4. (I) Scale-free fitting of neurons connectivity degree in SZ and HC networks. Connectivity scaling exponents were fitted with a mixed effect regression model detailed in Methods. The scaling exponents do not significantly differ between the two groups.

The number of active neurons within each network varied between 15 to 250 and regression analysis showed no difference in the mean number of active neurons per network between SZ and HC conditions (Figure S4A, mixed regression model detailed in Methods). However, because in most cases the measured FC-related variables (see below) correlated to the number of active neurons (Figure S4B), we considered this parameter as a covariable for almost all the multiple regression analyzes.

Network topology analysis in hiPSC-derived neuronal cultures, assessed by FC measurements

Since the underlying network topology frames neuronal interactions and signaling, assessing the FC properties of these systems is an indirect way of revealing and understanding the network’s structure and a direct way to interrogate the emerging network functioning.

To quantify network FC, we computed the Pearson’s correlation index for the Ca²⁺ signals of every pair of neurons in each network. As a first approach, we considered the entire recording time (4.7 min) and generated a FC matrix (or correlation matrix) displaying correlation indexes among neuron pairs (Figure 2E). A pair was considered as functionally connected when the correlation index was above 0.4 (defined here as positive connections) or below -0.4 (negative connections). For an absolute correlation value of 0.4 as a cut-off point, the functionally connected neurons reached 25% of the total possible connections, considering all networks (Figure 2F). The number of functional connections per neuron was obtained from the FC matrix. If the total number of connections per neuron (including positive and negative connections) were randomly determined (Figure 2G), the probability for a neuron to have “x” connections (connectivity degree) should follow a binomial distribution and for large enough populations, a Poisson distribution. In contrast, the probability distribution of the number of connections per neuron was right-skewed, resembling a ‘scale-free’ distribution (Figure 2H; also known as ‘long-tailed’ or ‘power-law’ distribution). This means that a large number of neurons have few active connections while a small number are hyper-connected (Figure 2G, H, I). This architecture suggests a complex modular organization that may optimize information processing and network robustness to damage [42] [43].

The scale-free fitting of neurons connectivity degree follows a power-law with a scaling exponent of -1.4 (Figure 2H). Interestingly, using trans-neuronal spread of rabies virus, a previous analysis of network topology in hiPSC-derived neurons demonstrated that the number of structural connections of these neurons also follows a scale-free distribution, with power -2 [19]. The latter supports the possibility that, through measures of FC, it is possible to explore the physiological properties of these neuronal networks, establishing a link between anatomical and functional connectivity.

To evaluate differences in functional topology between SZ and HC, we fitted a mixed linear model for the networks power-law scaling exponents, including a varying random intercept for cell line identity (id) and adjusting for the number of neurons and total possible number of connections in each network (see Methods). The functional topology of SZ networks does not deviate significantly from the HC networks behavior (Figure 2I).

FC in hiPSC-derived neuronal networks is dynamic and goes through reoccurring configurations

The FC analysis of resting networks described so far represents a measure of the average connectivity among pairs of neurons along the whole recording time (4.7 min). However, this approach does not allow to explore dynamic fluctuations of network connectivity that could occur within shorter periods of time.

To assess the temporal dimension of the FC in the hiPSC-derived networks, we applied a sliding-time-window correlation method [5] (Figure 3B.I; window width: 10.5 s or 70 frames) and computed the correlation matrix for every pair of time windows (wFC(t)); Figure 3B.II; custom code written in Python), obtaining a time-versus-time functional connectivity dynamics matrix (FCD) (Figure 3A). Matrix diagonal results from comparing the same time points, thus displaying full correlation. Points located adjacent to the diagonal (Figure 3A, white dotted squares), are also expected to present high correlation since they correspond to nearby, partially overlapping time windows. However, the squared blocks far away from the diagonal (Figure 3A, red dotted squares) suggest the reappearance of a previously visited FC configurations in a distant time point. This reveals that, during the registered time, network resting-state FC went through numerous and reoccurring configurations, rather than evolving in an arbitrary way. Remarkably, this observation resembles previously described FC dynamics results in human brains at resting conditions [13].

• Download figure
• Open in new tab

Figure 3. Dynamics of the resting-state functional connectivity (FC).

(A) A representative Functional Connectivity Dynamics matrix (FCD) was obtained from an HC network. This time-versus-time FCD(i,j) matrix is obtained by computing the Pearson’s coefficient of every FC(i) centered at a time “i” with every FC(j) centered at time “j”. Periods of lasting FC patterns appear as square blocks around the FCD diagonal (white dotted squares) and reoccurring patterns by square blocks distant from the diagonal (red dotted squares). (B) Scheme illustrating how FC meta-states (MSs) were obtained from an HC network. (B.I) ΔF is computed for every neuron in the network by subtracting the neuron’s baseline signal from the signal recorded at each time point. This plot is a graphical representation showing ΔF for 5 randomly selected neurons within the network, made up by 32 active neurons. A correlation matrix of neuron’s Ca²⁺signal is calculated within a given time-window (t) of shape (n, window width; n: number of neurons, window width = 70 frames = 10.5 sec). Then, the time window is shifted to time t+1 and the correlation matrix is recalculated. The last is successively repeated over the whole recording time. With this procedure, a windowed FC matrix (wFC(t)), with shape (n,n) is obtained for every time step. (B.II) Next, an independent component analysis (tICA) is performed along the temporal axis of the whole set of wFC(t), for every recorded network, and four independent connectivity patterns (CP) are obtained (B.III). Every wFC(t) can be described as a linear combination of these four CP and (B.III) shows the wFC(48) as an example. The coefficients multiplying each CP are obtained by linearly regressing the wFC(48) on the CPs. (B.IV) As we want to have a finite number of states (meta-states), the CP’s coefficients for each network were discretized and assigned to its respective quartile. The combination of these four coefficients describes a MS.

In spite of the huge differences in complexity of structural and functional connectivity of distant and dissimilar brain regions, compared to activity coupling in our neuronal networks, the preservation of a scale-free connectivity principle and the signs of configuration recurrence suggests that our model is suitable for exploring general properties of connectivity dynamics. Therefore, we next aimed to develop quantitative tools to further study FC dynamics in our hiPSC-derived networks. We modified a method previously designed to evaluate high-level dynamic properties of brain connectivity in SZ patients, through fMRI measurements [14]. To reduce the dimension of the wFC(t) matrix sets obtained from the different networks to a similar and smaller dimension (note that wFC matrices dimension depends on the number of active neurons in a particular network), we ran an independent component analysis (ICA) [27] per network, throughout the temporal dimension of its FC (Figure 3B.II). This computational method allows separation of a complex signal into additive components [27]. Four different and independent FC configurations, defined here as correlation patterns (CP), were identified. By expressing each wFC(t) data in terms of these four CP, we obtained four coefficients or “weights”, each one associated to a specific CP. The weights describe how “enriched” is the wFC(t) of each of the different CP (Figure 3B.III). To have a finite number of FC configurations, the weights were discretized into quartiles allowing grouping similar connectivity configurations (Fig 3B. IV). The unique combination of four discretized weights defined a meta-state (MS), borrowing the term coined by Robyn Miller [14].

FC in SZ is less flexible and slower in rearranging different configurations

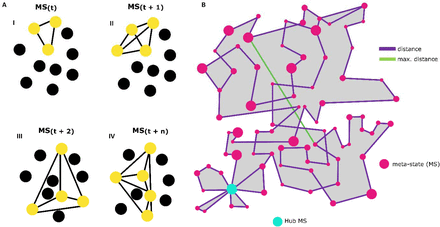
By studying neuronal functional relationships in our in vitro model, we may address the question of whether FC dynamic alterations observed in SZ patients’ brains by fMRI, can be seen during the development of neural networks, in a completely different spatiotemporal domain. Using the described methodology, we obtained the FC MSs for each network. A set of connectivity variables (listed and defined in Methods) were quantified and differences between- and within-groups were assessed using mixed linear regression modeling. Figure 4 aims to clarify the definition of these variables. Figure 4A illustrates examples of different MSs visited by a network along time. The meaning of the measured FC variables is explained in Figure 4B.

• Download figure
• Open in new tab

Figure 4. Functional connectivity (FC) flow and FC-related dynamic variables.

(A) Schematics representing four possible functional connectivity meta-states (MS), corresponding to specific activity configurations of the neurons conforming the network; each circle represents a neuron. Yellow circles are active, functionally connected (lines) neurons at different times. (B) Functional connectivity flow in a network. Pink circles represent the different visited MSs and circle size denotes the uninterrupted time spent by the network in this configuration. Purple lines represent a distance (Manhattan distance) in the space where the different MSs inhabit. The length of lines connecting MSs illustrates how different are consecutive configurations. Each inflection point corresponds to a transition from an MS to the next one. The green line represents the maximum distance between two successive MSs and illustrates the network’s ability to switch in just one step between two configurations that are as different as possible. The light blue circle indicates an MS that is visited with recurrence, a Hub MS. The grey area corresponds to the dynamic range, a global indicator of the diversity of the accessible MSs. The length of the trajectory of the purple line corresponds to the total traveled distance.

We observed a reduction in the number of different MSs visited by SZ networks (Figure 5A), suggesting a more limited repertoire of accessible configurations, compared to HC networks. We also measured the number of times that networks changed from one MS to another and the mean uninterrupted time spent in a MS. SZ networks change fewer times from one MS to another (Figure 5B) and spend longer at the same MS (Figure 5C), thus they are less dynamic. On the other hand, HC networks can transit to more different (distant) configurations in one step (maximum distance between successive MSs, Figure 5D) than SZ networks. This means that the latter have less potential to fast switching between distant FC configurations, displaying less flexibility. We also calculated the total travelled distance within the MSs-inhabited space, calculated as the sum of the distances between successive MSs through the whole recording time (Figure 5E), finding that it was lower in SZ (Figure 5F). Finally, we evaluated the dynamic range, which is formally a measure of the size of the space containing the different MSs, by calculating the Manhattan distance between the farthest MSs visited along the whole trajectory (Figure 5G). We must bear in mind that the dynamic range calculations are relative to network’s specific CPs. Therefore, this measurement reflects how much the space where the different MSs inhabit is expanded or contracted with respect to the network’s own intrinsic “motion possibility space”. This can be understood as the potential of a network to flow through more diverse connectivity configurations. We observed a reduced FC dynamic range in SZ networks (Figure 5G). This result is consistent with the lower number of different realized MSs and the reduced total traveled distance in SZ networks, as a lower dynamic range implies a decrease in FC motion potential. These findings suggest that resting-state SZ networks exploring available FC configurations less thoroughly and reorganize less rapidly compared to HC. Overall, these results point to a reduction of FC dynamism and flexibility in SZ networks, involving speed and exploration potential.

• Download figure
• Open in new tab

Figure 5. Functional Connectivity in SZ-derived networks is less dynamic than for HC cultures.

(A) SZ networks visited a lower number of different meta-states (MSs). (B) SZ networks change fewer times from one MS to another during the recorded time, spending longer uninterrupted time within the same MS (C). (D) The maximum distance between successive MSs is also reduced in SZ neuronal networks. (E) A graphical representation of how FC travels within the space inhabited by the MSs, considering the distance between successive visited MSs. The plot indicates the cumulative traveled distance, measured as the total traveled distance at each time point (x). (F) The overall distance traveled through the MSs space, calculated as the sum of the L1 distances between consecutive MSs, is reduced in SZ networks. (G) The intrinsic dynamic range, measured as the Manhattan distance (L1) between the most distant MSs, is reduced in SZ networks. For each dependent variable (Y-axis), the SZ (diag) effect from the regression model, (Materials and Methods), is indicated.

SZ networks display a reduced number of recurrent FC meta-states (hub meta-states)

As mentioned, neuronal networks went through different FC configurations that reoccur during the acquisition time (Figure 3A, FCD matrix). We computed the number of different MSs that were re-visited by each neuronal network. In whole brain fMRI FC analysis these recurrent MSs have been named as “hub meta-sates” [14]. Our results show that SZ networks display a lower number of hub MSs (Figure 6A) and visit hub MSs less often than HC networks (Figure 6B) but spent longer uninterrupted time in them (Figure 6C).

• Download figure
• Open in new tab

Figure 6. SZ-derived networks visit a lower number of different hub states but remain longer times within them.

(A) The number of different visited hub meta-sates (MSs) is lower in SZ networks. (B) SZ networks visit hub MSs less often than HC networks, but (C) spend longer uninterrupted time in the same hub MS. For each dependent variable (Y-axis), the SZ (diagnosis) effect from the regression model, detailed in the Methods and Materials section, is indicated. The p-values of the coefficients meet the requirement of p <0.05.