ABSTRACT
SARS-CoV-2 vaccines provide not just high protection against infection to the vaccinated individual but also provide indirect protection to its surroundings by blocking further transmission. Divergent results have been reported on the effectiveness of the SARS-CoV-2 vaccines. Here, we argue that this divergence is due to the fact that the analyses did not take into account the indirect protection. Using a novel heterogenous infection model and real-world data, we demonstrate that heterogeneous vaccination rates among families and communities, and the study design that is used, may significantly skew the vaccine effectiveness estimations. We show that estimations of a vaccine with 85% effectiveness will vary between marked underestimation of ∼70% and overestimation of ∼95% depending on the number of interactions between vaccinated and unvaccinated individuals.
INTRODUCTION
Hundreds of millions of individuals have been infected with the SARS-CoV-2 virus, and millions of them died as a result of the infection since it was first detected in China at the end of 2019. In response, several companies and research institutions developed vaccines to help suppress the pandemic, and less than a year after identifying of the virus, several clinical trials reported results of proven vaccine efficacy [1, 2]. The randomized clinical trials of the Pfizer/BioNTech and Moderna vaccines showed vaccine efficacy of around 95% in the first months after the second dose; however, the studies had relatively low numbers of infected individuals, and this level of efficacy can only be regarded as a proxy to the real-world vaccine effectiveness across divergent populations, demographics, and clinical features.
By the end of 2020, many countries launched mass vaccination campaigns. The data collected through these mass vaccination campaigns was used to evaluate the effectiveness of the vaccines in a wide range of populations [3–9]. Individual-level study designs for vaccine effectiveness (VE) evaluation can be split into two main approaches: (1) A population-based approach (PB), where the number of vaccinated and unvaccinated infections are counted after correcting for possible confounders [3]; (2) A secondary infections approach (SI), which allows to overcome a major limitation of the first approach of unknown exposure. In this approach, infections are counted after a known exposure, such as secondary household infections [4]. Interestingly, when examining the VE estimations from studies that use each approach, there are major differences (Supplementary Table 1). In PB studies, VE was usually estimated at 90%-95%, while in SI studies, much lower VE estimations are usually reported (60%-80%). Moreover, observational studies in nursing home residents reported varying VE levels ranging from 53% to 92% against SARS-CoV-2 infection [10–14]. There could be numerous reasons that may explain the differences; however, we hypothesize that the main reason is a difference in the number of interactions with other vaccinated individuals that is different between the two settings.
Our hypothesis is based on one feature of the vaccines that has been broadly neglected in current VE studies. While the vaccines were designed mainly to reduce symptomatic disease, severe disease, and death, studies have shown that they also provide efficient transmission-blocking. A study from Sweden found that the number of immune members in a family was negatively correlated with the likelihood of incidence of infection of non-immune family members [15]. Similarly, a study from Israel found reduced infection rates in communities as vaccination rates increased [16]. Previous studies before COVID-19 have shown how interference, the potential outcomes of one individual are affected by the treatment assignment of other individuals, can affect VE estimations [17]. It seems that an underlying assumption made by the COVID-19 VE studies is that there is no interference, which is an unfounded assumption.
Here, we demonstrate how the indirect protection affects VE estimations. We develop a novel infection model, and use it to demonstrate that this bias is proportional to the rate of mixing between vaccinated and unvaccinated individuals. To illustrate this bias in real-world settings, we employ a dynamic physical model [18, 19] and real data from Israel [20, 21] to estimate VE in Israel under different assumptions of interference, i.e., under different scenarios of mixing between vaccinated and unvaccinated individuals. Our analyses show that different assumptions may lead to significant under- or over-estimations and might explain the differences in estimations between the different study design approaches.
METHODS
To quantify how VE estimations are sensitive to the prevalence of interactions between vaccinated and unvaccinated individuals, we developed a heterogenous infection model (HIM). The HIM is a network composed of multiple cliques, close contact networks, which might resemble household interactions. Nodes in the clique may be ‘vaccinated’ or ‘unvaccinated’. For each vaccinated node, we define γ as the fraction of edges it has with unvaccinated nodes. We further define ⟨γ⟩ as the average of all γ values in the network. A ⟨γ⟩ = 0 in the HIM represents a network where the vaccinated and the unvaccinated populations are completely distinct as there are no close interactions between them. As ⟨γ⟩ increases, there is more mixture between the two populations.
The cliques are weakly connected with each other. We denote δ as the ratio between infections happening inside the clique versus infections happening outside of the clique. Around half of all infections are household infections [22], so a logical δ is 1. We also define α as the probability of transmitting the virus; β as the reduced risk of infection for protected individuals (vaccinated or previously infected), similar to 1 minus VE. Importantly, we assume that protected individuals also further transmit at a β rate compared to unvaccinated. Finally, Nin is the number of nodes in each clique, and Nout is the sum of nodes in all other cliques in the network. The parameters used in the HIM are summarized in Table 1.
To simplify the functions, we further define additional parameters of the number of vaccinated and unvaccinated edges, for each vaccinated and unvaccinated node, inside and outside of the clique. Table 2 summarize these parameters.
The individual risk of infection is the sum of infections inside the clique plus infections from outside the clique: Infection risk from inside the clique depends on the number of vaccinated and unvaccinated nodes in the clique; Infection risk from outside the clique depends on the fraction of vaccinated nodes outside the clique. Equations (1) and (2) present the infection risk for vaccinated nodes and for unvaccinated nodes:

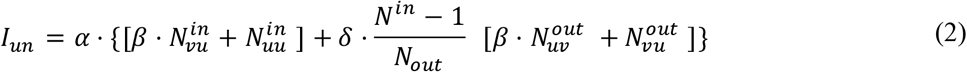
Finally, we can calculate the observed VE, which we denote here as  , by dividing (1) by (2):
, by dividing (1) by (2):
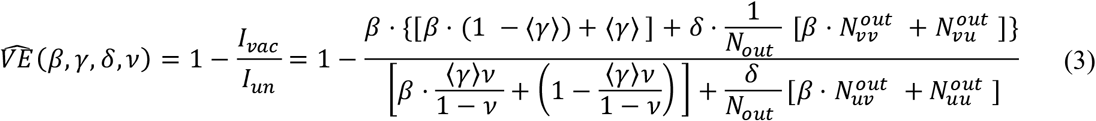
We can see that the equation for  is dependent β, γ, δ and v, but are independent on Nin (the size of the clique) and α (the probability of transmission). To summarize, HIM is a relatively simple model that simulates infections in a population with non-uniform vaccination rates and at heterogenous circuits of infection risks. It takes into account the risk of infection in vaccinated households and allows to quantify the population observed VE, corrected by the interference, as opposed to the individual-level VE.
is dependent β, γ, δ and v, but are independent on Nin (the size of the clique) and α (the probability of transmission). To summarize, HIM is a relatively simple model that simulates infections in a population with non-uniform vaccination rates and at heterogenous circuits of infection risks. It takes into account the risk of infection in vaccinated households and allows to quantify the population observed VE, corrected by the interference, as opposed to the individual-level VE.
RESULTS
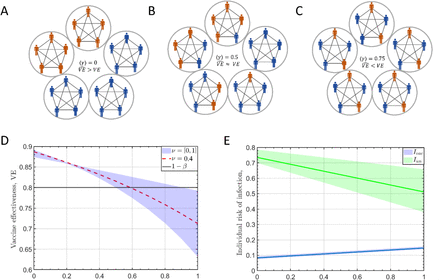
We developed a heterogenous infection model (HIM) that allows to simulate infections, where there are both household infections and non-household infections. The HIM model allows to calculate an observed vaccine effectiveness (VE) as a function of the mixture of vaccinated and unvaccinated individual, which is defined with ⟨γ⟩ (full details in Methods). For illustration purposes of HIM, we present three possible mixtures described using three networks. In all networks, there is a similar amount of vaccinated and unvaccinated nodes, and there are precisely four close connections for each individual (Nin = 5, Nout = 20) (Figure 1A-C). The only difference between the three networks is the dispersal of the vaccinated and unvaccinated nodes: in network (A), there is complete segregation between vaccinated and unvaccinated nodes (⟨γ⟩ = 0). This network might simulate nursing homes that were vaccinated early, while the majority of the rest of the population was not yet vaccinated. In network (B), for each vaccinated node, half of the edges are to vaccinated nodes and half to unvaccinated nodes (⟨γ⟩ = 0.5). In network (C), each vaccinated node is connected to one vaccinated node and three unvaccinated nodes (⟨γ⟩ = 0.75). Network (C) might simulate households where two members are vaccinated (e.g., parents) and two are not (e.g., children).
A-C. Orange individuals are vaccinated nodes, blue individuals are unvaccinated nodes. Each circle is a tightly connected clique. Weak interactions with individuals outside of the clique. D. the observed VE, 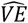 as a function of γ, for δ = 1 and β = 0.2: Blue band:
as a function of γ, for δ = 1 and β = 0.2: Blue band:  for v = [0,1]; Red dashed line: v = 2/3; Grey solid line: 1 − β = 0.8. E. the infection risk, I, for Nin = 5, α = 0.1 and δ = 1 and v = 0.7 ± 0.3; Blue band: Ivac; Green band: Iun. The width of the band originates from the variability of v.
for v = [0,1]; Red dashed line: v = 2/3; Grey solid line: 1 − β = 0.8. E. the infection risk, I, for Nin = 5, α = 0.1 and δ = 1 and v = 0.7 ± 0.3; Blue band: Ivac; Green band: Iun. The width of the band originates from the variability of v.
For each of the networks we count the number of infections, I, and calculate 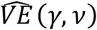 for β = 0.2 (VE = 80%), α = 0.1 and δ = 1. Using the equations descried in the HIM, for a scenario where two-thirds of the population are vaccinated (v = 0.4) we find that the risk of infection in (B) for vaccinated nodes is 0.12 and 0.62 for unvaccinated nodes, which translates to
for β = 0.2 (VE = 80%), α = 0.1 and δ = 1. Using the equations descried in the HIM, for a scenario where two-thirds of the population are vaccinated (v = 0.4) we find that the risk of infection in (B) for vaccinated nodes is 0.12 and 0.62 for unvaccinated nodes, which translates to  , similar to the input VE. However, in (A) and (C) we see a diversion from the input VE: in (A) risk for vaccinated is 0.083 and 0.74 for unvaccinated, which translates to an overestimation of almost double reduced risk (89%), and in (C) these numbers are 0.13 and 0.56, respectively, which translate to an underestimation (75%). Generally, we observed that for γ around 0.5-0.7 the input VE is similar to
, similar to the input VE. However, in (A) and (C) we see a diversion from the input VE: in (A) risk for vaccinated is 0.083 and 0.74 for unvaccinated, which translates to an overestimation of almost double reduced risk (89%), and in (C) these numbers are 0.13 and 0.56, respectively, which translate to an underestimation (75%). Generally, we observed that for γ around 0.5-0.7 the input VE is similar to 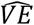 (Figure 1D); Lower ⟨γ⟩ levels produce overestimations of
(Figure 1D); Lower ⟨γ⟩ levels produce overestimations of 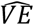 up to 90%, and higher ⟨γ⟩ levels produce underestimations towards 70%. Interestingly, as ⟨γ⟩ increases, and there is higher mixture of vaccinated and unvaccinated individuals, the infection risk of the unvaccinated population decreases (Figure 1E). This is due to the indirect protection enjoyed by unvaccinated individuals, as they have more interactions with vaccinated individuals.
up to 90%, and higher ⟨γ⟩ levels produce underestimations towards 70%. Interestingly, as ⟨γ⟩ increases, and there is higher mixture of vaccinated and unvaccinated individuals, the infection risk of the unvaccinated population decreases (Figure 1E). This is due to the indirect protection enjoyed by unvaccinated individuals, as they have more interactions with vaccinated individuals.
In summary, we show here that the rate of interactions between vaccinated and unvaccinated individuals significantly alters VE estimations.
We next attempted to model the infections occurred in the real world and show how calculations of VE can be skewed based on different assumptions regarding ⟨γ⟩. We previously developed a spatial-dynamic Monte Carlo algorithm that was able to accurately predict infection dynamics in Israel. In this work, we expand this model to include more complex interaction networks. In contrast to the basic HIM, in the real world, interaction networks are much more complicated. Therefore, we now use a three-circuits interaction network that aims to mimic interactions of close contact household members, lower level contact with the immediate community, and low level of remote contacts with a larger community group. Around half of all infections in Israel are in households [22]. Therefore, we use it as a guide for the infection dynamics in our model (full details about the model are available in Supplementary Methods).
Using this model, we simulated the spread of COVID-19 infections in Israel from the beginning of the vaccination campaign on December 20, 2020, for ten different mixing scenarios between vaccinated and unvaccinated individuals. In all scenarios, vaccination rates across communities are based on real-world data [21], but the scenarios differ in how vaccines are dispersed across each community (more details are available in Supplementary Methods).
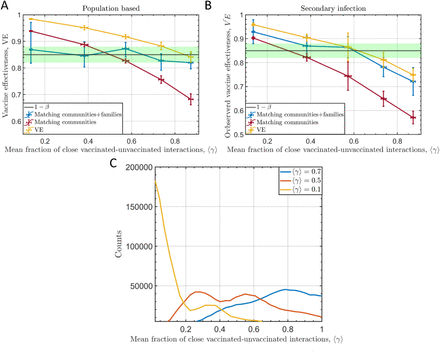
The scenarios simulated infections throughout Feb 2021. In each date we calculated the observed vaccine effectiveness,  using the population-based approach (PB) and the secondary infection approach (SI). The analysis showed a clear negative correlation between
using the population-based approach (PB) and the secondary infection approach (SI). The analysis showed a clear negative correlation between 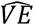 and ⟨γ⟩ for both the PB and SI analysis (Figure 2A-B). Interestingly, in the PB analysis we observed that for all the range of ⟨γ⟩, up to almost random assignment of vaccinees across the population (⟨γ⟩ = 0.9),
and ⟨γ⟩ for both the PB and SI analysis (Figure 2A-B). Interestingly, in the PB analysis we observed that for all the range of ⟨γ⟩, up to almost random assignment of vaccinees across the population (⟨γ⟩ = 0.9),  was higher than the input VE, which was 85%. The explanation for this result is that there was high heterogeneity in vaccination uptake across communities in Israel (Supplementary Figure 1). While the majority of communities have reached high vaccination rates rapidly, there where some communities with low vaccination uptake, leading to a bimodal distribution of vaccinations rates, and in turn of ⟨γ⟩ (Figure 2C). In those low vaccined communities, there is low indirect protection, and the heterogneity across the population is what is causing the high overestimation across the whole range of ⟨γ⟩. This result should warrant that crude VE estimations in heterogenous population are bound to overestimate VE.
was higher than the input VE, which was 85%. The explanation for this result is that there was high heterogeneity in vaccination uptake across communities in Israel (Supplementary Figure 1). While the majority of communities have reached high vaccination rates rapidly, there where some communities with low vaccination uptake, leading to a bimodal distribution of vaccinations rates, and in turn of ⟨γ⟩ (Figure 2C). In those low vaccined communities, there is low indirect protection, and the heterogneity across the population is what is causing the high overestimation across the whole range of ⟨γ⟩. This result should warrant that crude VE estimations in heterogenous population are bound to overestimate VE.
A. Estimations of the observed VE as a function of ⟨γ⟩ using population-based analysis. Yellow line: crude analysis; red line: with matching of vaccinated and unvaccinated individuals in each statistical area; blue line: matching for statistical areas and additionally filtering out individuals in close-contact circuits with more than 50% vaccination. B. Similar to A, but for secondary infection-based analysis. C. Distribution of γ in all vaccinated individuals on February 1 in three scenarios of mixing vaccinations across the population.
When using the SI approach for calculating  , we observed an even stronger negative correlation between
, we observed an even stronger negative correlation between  and ⟨γ⟩. In this analysis we only consider infections within the close-contact circuit, which is similar to a situation of δ = 0 in HIM. Thus, low ⟨γ⟩ represents a scenario where most close-contacts circuits are partially vaccinated (i.,e. a family with only one parent vaccinated), and high ⟨γ⟩ represents a scenario where most close-contact circuits are either fully vaccinated or not vaccinated at all. Similarly to the HIM-based analysis we see in our real-world modeling that if ⟨γ⟩ > 0.5, the observed VE is lower than the input VE.
and ⟨γ⟩. In this analysis we only consider infections within the close-contact circuit, which is similar to a situation of δ = 0 in HIM. Thus, low ⟨γ⟩ represents a scenario where most close-contacts circuits are partially vaccinated (i.,e. a family with only one parent vaccinated), and high ⟨γ⟩ represents a scenario where most close-contact circuits are either fully vaccinated or not vaccinated at all. Similarly to the HIM-based analysis we see in our real-world modeling that if ⟨γ⟩ > 0.5, the observed VE is lower than the input VE.
We next performed the same analysis, but this time VE was calculated by matching the number of vaccinated and unvaccinated in each community, which eliminates the heterogeneity in vaccination rates among communities, and is similar to a matched analyses of VE, where individual-level data is available (Figure 2A-B). After matching for both SI and PB analyses,  could be both under- and overestimated. The estimations of
could be both under- and overestimated. The estimations of 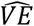 in the matched analysis was from ∼60% to 95%, depending on ⟨γ⟩. The input VE was only obtained at for ⟨γ⟩ at levels around 0.5 and 0.3 for PB and SI, respectively. The reason why matching is still insufficient to retrieve the input VE stems from the additional circuits we added in the modelling that aim to mimic household contacts. This creates heterogeneity of ⟨γ⟩ at the close contacts-level, not just at the community-level. To overcome this issue, we derived an additional analysis that considers the level of mixing. Since it is not simple to adjust for different ⟨γ⟩ levels in real-world data for PB analysis, we performed the analysis by including only close-contact circuits with over 50% vaccinated individuals. This analysis showed that for PB, is it possible to get relatively accurate estimations of VE with relatively simple approach. Of note, in SI analysis, both γ and v can be theoretically obtained for each family (and δ = 0), therefore,
in the matched analysis was from ∼60% to 95%, depending on ⟨γ⟩. The input VE was only obtained at for ⟨γ⟩ at levels around 0.5 and 0.3 for PB and SI, respectively. The reason why matching is still insufficient to retrieve the input VE stems from the additional circuits we added in the modelling that aim to mimic household contacts. This creates heterogeneity of ⟨γ⟩ at the close contacts-level, not just at the community-level. To overcome this issue, we derived an additional analysis that considers the level of mixing. Since it is not simple to adjust for different ⟨γ⟩ levels in real-world data for PB analysis, we performed the analysis by including only close-contact circuits with over 50% vaccinated individuals. This analysis showed that for PB, is it possible to get relatively accurate estimations of VE with relatively simple approach. Of note, in SI analysis, both γ and v can be theoretically obtained for each family (and δ = 0), therefore,  can be adjusted more easily in real-world data.
can be adjusted more easily in real-world data.
DISCUSSION
We demonstrated here that VE estimations are sensitive to the dispersion of vaccinations across the population. We found that the level of mixing between vaccinated and unvaccinated individuals can completely alter the observed VE. High level of mixing creates indirect protection to unvaccinated individuals, which in turn leads to underestimation of VE, while low level of mixing leads to additional protection to the already protected individuals, and in turn to overestimation of VE. Regardless of what is the real mixing between vaccinated and unvaccinated, which we assume is far from random, it is clear from our analyses that the observed VE can significantly differ from the real individual-level protection offered by the vaccine.
It is not simple to estimate the level of mixing in the population. However, we note that during the time of first estimations of VE coming from Israel [3], Israel was mostly under a lockdown that was imposed between January 8, 2021, and February 9, 2021. Under the lockdown there were limited interactions overall, and especially between the vaccinated elderly population and the rest of the population which were vaccinated later. It is therefore safe to assume that ⟨γ⟩ at the time of the study was trending towards 0, or at least much lower than later on. Based on this, we argue that the high VE reported 95% for adults over 70 years old [3] is grossly overestimated. Furthermore, the lower VE reported for the 40-69 years old group in that study (90%) is a result of the higher mixing rate of that group. Later on, Israel imposed “green passports”, which limit entrance of unvaccinated individuals to crowded places. This is another measure that reduces vaccined-unvaccined interactions and may again skew towards overestimation of VE.
On the other hand, we argue that study designs of secondary household infections underestimate VE. Gazit et al. used this approach to estimate VE in Israel and found VE to be 80% [4]. In households, especially in a country with relatively big families as in Israel, most interactions of vaccinated individuals are with unvaccinated children that were not vaccinated at the time of the study. This translates to high ⟨γ⟩ levels, and as we show this leads to significant underestimation. We note that some of the lower VE in household infections can be attributed to the prolonged exposure, and in theory, the vaccination is less effective in such scenario.
Our study is not the first to caution about VE estimations confounded by indirect protection. Previous studies developed a causal inference framework with interference to deal with this issue [17]. Interestingly, although this issue is well known, in our literature review of VE studies for COVID-19, we did not identify any study that takes this issue into account. We believe that our heterogenous infection model (HIM) provides a novel and relatively simple framework for dealing with vaccine interference, and, as we show here, can be implemented in real-world settings. The HIM is structured to differentiate between different types of interactions (close and remote), and therefore, better represents real-world infection networks.
In conclusion, we argue here that observed VE estimations of 90%-95% and 80% stems from a vaccine that probably provides individual-level protection of around 85%. We suggest that by adjusting to the fraction of unvaccinated individuals in a household, in addition to demographic and clinical features, it is possible to reduce the bias when estimating VE. We hope that future studies will take into account the possible bias we highlight in this study and attempt to correct for it, as the rate of effectiveness of the vaccines have high impact on strategies for controlling the spread of the pandemic.
Supplementary Methods
In this work, we use a diffusive Monte-Carlo (MC) model originally introduced by De-Leon and Pederiva [18, 19] to model the spread of the COVID-19 in Israel in the presence of effective vaccines from December 2020 until March 2021, and as a result, to estimate the observed vaccine effectiveness. As opposed to other infection models, such as the Susceptible Infected Removed (SIR) [23, 24], this particle model enables us to distinguish between different age groups and treat each one separately, assuming that the infection occurs throughout the population simultaneously. Furthermore, a particle model can be adjusted to the actual rate of population immunization. This model enables us to accurately examine the different effects of the vaccine on subgroups of the vaccinated population and the entire population. We used numerical simulations that consist of 9 · 106 particles (which simulates the number of residents in Israel), where each particle has a number from 1 to 9 · 106 under the assumption of three infection circuits (arranged according to the likelihood of infection from high to low): a household infection cycle involving five people (which is the average in Israel); community based-infection, an infection cycle of 25 people; and infections in a remote community – an infection circle of 125 people. We define the model to generate half of all infections in the simulation to occur within households, by assuming that particle 1 interacts mostly with particles 2-5 (i.e., particles 1-5 resemble a household, so any group of 5 particles). Still, there is almost no contact between 1 and particle number 2000.
Modeling the spread of COVID-19 in the presence of effective vaccines
For modeling the spread of COVID-19 in the presence of effective vaccines, it is necessary to differentiate between Rt (the theoretical reproduction number of the virus) and Re (the effective reproduction number of the virus). Rt estimates the number of encounters between carriers and healthy individuals that would have resulted in an infection if the vaccines had not been available and is defined by how contagious the current variant is. Re is affected by vaccination rates and protection offered by the vaccines, i.e., the vaccine’s effectiveness. In this work, following the easing of social restrictions in Israel in February 2021, we estimate the theoretical Rt in Israel from January 2021 until February 2021 to be 1.2 [25]. It is important to note that in contrast to R0, the basic reproduction rate, Rt considers the non-pharmaceutical interventions (NPIs) used in Israel to control the spread, notably mandatory isolation for individuals with confirmed infection and to those exposed to a confirmed case, and additionally mask covering indoors.
To model vaccine effectiveness, we assumed the protection from the vaccine starts seven days after the first dose and reached its maximum after seven days from the second dose [3, 26].
Adjustment for real-world data
We use here publicly available data from Israel [21] for 1,578 different statistical areas, which are regions defined by the Central Bureau of Statistics of Israel and include regions of about 5,000 individuals on average. Using this data allows us high resolution of the heterogeneity in vaccinations uptake. We use the regional vaccination data between the end of December 2020 and March 2021 to calculate the daily number of confirmed cases in Israel for each statistical area. We assume that most infections are local, and half of the infections occur at home, and only less than 1% of the infections occur outside the statistical area.
We created ten different scenarios which differed in the mixing between vaccined and unvaccined individuals/particle such that for each scenarios, the order of immunization within the statistical area ranges from absolute randomness (⟨γ⟩ = 1), to immunization according to families (⟨γ⟩ = 0), which affect the number of interactions between vaccinated and unvaccinated (different γ levels). Consequently, the vaccination order within each statistical region is important since the greatest chance of infection is between two adjacent serial numbers. Since not all populations were vaccinated simultaneously in reality, ⟨γ⟩ changes through time. As a result, we define for every day a mean value of γ, ⟨γ(t)⟩, which represents the daily average percentage of vaccined-unvaccinated interactions for the vaccinated population.
Note that we assume that half of all infections occur in the first infection circuit (at home). Therefore, the contribution from the second and third circuits is lower than the contribution from the first circuit.
Calculation of the observed vaccine effectiveness
For calculating VE, we defined the VE, seven days after the second dose for each day as:
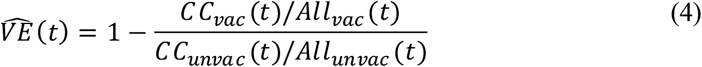 where:
where:
CCvac(t) - daily number of particles who became infected seven days or more after receiving the second dose of the vaccine.
CCnon(t) - daily number of particles who became infected before receiving the first dose of the vaccine.
Allvac (t) - daily number of fully vaccinated particles in the population (seven days or more from receiving the second dose of the vaccine).
Allnon (t) - daily number of unvaccinated people in the population (before receiving the first dose of the vaccine).
We used two methods for calculating the daily VE for each vaccination scenarios using two different methods (Figure 2). The crude approach, which is just counting daily infections, and the matched approach, where similar amount of vaccinated and unvaccinated individuals are chosen randomly from each statistical area. Matching across statistical areas reduces the effect of the heterogeneity in vacciations uptake, and in theory should eliminate the overestimation caused by this. However, since our model consists of a ‘family’ circuit, the matching is insufficient for avoiding the overestimation. We note that this is most probably true. For example, if one partner is vaccinated, most likely, the other partner will be vaccinated as well.
SUPPLEMENTARY DATA
List of vaccine (2 dose of BNT162b2 vaccine) effectiveness estimations studies. PB: population-based approach; SI: secondary infection approach.
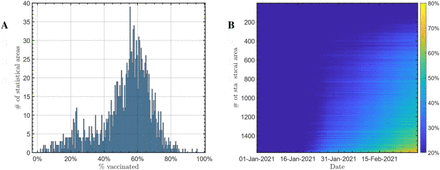
The vaccination campaigns started by vaccinating older individuals before moving to younger populations. Further, there is a significant association between vaccine uptake and socioeconomic status (SES) and other factors [29]. In Israel, based on the data from [20] for the population of each statistical area and the data from [21] for the daily A vaccinated people for each of the 1,578 statistical areas, we can calculate, on a daily basis what is the percentage of the population which is vaccinated with two doses of vaccine. We found that the distribution of the percentage of the population that was vaccinated with two vaccine doses on April 1, 2021, manifested in a somewhat bi-modal distribution of vaccine uptake across the population: while in the majority of the statistical regions (>90%), we observe a normal distribution around 60% with standard deviation of 10% 4 months after the beginning of the campaign, in 10% of regions, the vaccination rate was only <25% (Figure 3A). This heterogeneity in vaccine uptake is even more pronounced in the first 45 days of the vaccination campaign. A. Distribution of the rate of fully vaccinated individuals in 1,578 statistical regions in Israel on April 1, 2021. B. Daily vaccination rates in Israel for each of the 1,578 statistical. Rows represent statistical regions, columns represent days, and the color is the cumulative percentage of vaccinated individual in the region.
ACKNOWLEDGMENTS
DA is supported by the Azrieli Faculty Fellowship and is a Deloro Fellow.
We thank Yaniv Erlich, Barak Rave and Michael Geller for fruitful discussions.