Association of effective circulating blood volume with sublingual RBC velocity and microvessel pressure difference in anesthetized individuals: A clinical investigation and computational fluid dynamics modeling

Athanasios Chalkias, Michalis Xenos
doi: https://doi.org/10.1101/2022.05.09.22274826

ABSTRACT

Background Although changes in effective circulatory volume may affect microcirculatory red blood cell (RBC) velocity and oxygen extraction ratio, no systemic variable has been consistently associated with hemodynamic coherence. We therefore evaluated the association between mean circulatory filling pressure and microcirculatory perfusion and oxygenation.

Methods This analysis included anesthetized individuals in steady-state physiology. We assessed the correlation of mean circulatory filling pressure analogue (Pmca) with sublingual microcirculation and RBC velocity using SDF+ imaging and a modified optical flow-based algorithm. We also reconstructed the 2D microvessels and applied Computational Fluid Dynamics (CFD) to evaluate the correlation of Pmca and RBC velocity with the obtained pressure and velocity fields in microvessels from CFD [pressure difference (Δp)].

Results Twenty adults were included in the study, of whom 12 (60%) were men and 8 (40%) were women, with a median age of 39.5 years (IQR 35.5-44.5). Sublingual velocity distributions were similar and followed a log-normal distribution. A constant Pmca value of 14 mmHg was observed in all individuals with sublingual RBC velocity of 6-24 μm sec-1, while a Pmca <14 mmHg was observed in those with RBC velocity >24 μm s-1. When Pmca ranged between 11 mmHg and 15 mmHg, Δp fluctuated between 0.02 Pa and 0.1 Pa.

Conclusions These data suggest that the intact regulatory mechanisms may maintain a physiological coupling between systemic hemodynamics and tissue perfusion and oxygenation when Pmca is 14 mmHg.

HIGHLIGHTS

  • Changes in effective circulatory volume may affect microcirculatory red blood cell (RBC) velocity and oxygen extraction ratio, but no systemic variable has been consistently associated with hemodynamic coherence

  • We found that a mean circulatory filling pressure analogue (Pmca) value of 14 mmHg maintains sublingual RBC velocity at 6-24 μm s-1

  • A Pmca <14 mmHg is observed in individuals with RBC velocity >24 μm s-1

  • Microvessel pressure difference is maintained constant when Pmca ranges between 11 mmHg and 15 mmHg

  • These findings imply that tissue oxygenation can be maintained in very low RBC velocities

  • Therapeutic strategies and translational research beyond optimizing macrohemodynamics and microcirculatory flow are required, including normalizing red blood cell velocity

Background Hemodynamic coherence is not well-investigated and no systemic hemodynamic variable has been consistently correlated with microcirculatory perfusion and tissue oxygenation.

Translational Significance The present study provides a novel method to monitor hemodynamic coherence and tissue perfusion, which can aid in the identification of novel hemodynamic phenotypes and enhance microcirculation-guided therapeutic strategies, optimizing local delivery of oxygen. Our findings also imply that (1) tissue oxygenation can be maintained in very low red blood cell velocities; and (2) therapeutic strategies and translational research beyond optimizing macrohemodynamics and microcirculatory flow are required, including normalizing red blood cell velocity.

1. INTRODUCTION

Physiological hemodynamic coherence is the condition in which the systemic hemodynamic variables are translated into effective microcirculatory perfusion and oxygen delivery to the parenchymal cells. This requires normal physiology and intact compensatory mechanisms to regulate oxygen transport to tissue. Although hemodynamic coherence was first described in 1850, only recently has it been studied in critically ill patients. Nevertheless, its characteristics in steady-states are not well-investigated and no systemic hemodynamic variable has been consistently correlated with microcirculatory perfusion and tissue oxygenation.

As the main role of the venous system is to serve as a capacitance to maintain filling of the heart and cardiac output (CO), assessment of mean circulatory filling pressure (Pmcf) is a basic parameter of functional hemodynamic monitoring. Mean circulatory filling pressure is the blood pressure throughout the vascular system at zero flow [1]. Based on a Guytonian model of the systemic circulation, an analogue of Pmcf (Pmca) can be derived that adequately follows intravascular volume status [2,3], its measurements are automatic, and can characterize the hemodynamic response to treatment modalities [4,5].

Decreases in effective circulatory volume may affect microvascular red blood cell (RBC) velocity resulting in insufficient oxygen extraction ratio (O2ER) [6,7]. On the other hand, fluid or vasopressor administration may increase the stressed volume, eventually increasing cardiac output (CO) and changing RBC velocity [8,9]. Considering that CO is determined by venous return, we hypothesized that the effective circulating blood volume, and thus Pmca, is associated with effective microcirculatory perfusion. This could provide an integrative monitoring tool for assessing hemodynamic coherence and performance, especially when such advanced monitoring methods are not available.

In the present study, we aimed to elucidate our hypothesis in greater depth. To this end, we evaluated the association of Pmca and other determinants of venous return with sublingual microcirculatory variables, RBC velocity, and O2ER in anesthetized adults with steady-state physiology. In addition, Computational Fluid Dynamics (CFD) models were developed using clinical data to evaluate the velocity and pressure fields in microvessels.

2. MATERIAL AND METHODS

2.1 Design

This explorative investigation included individuals who were excluded from a previous prospective observational study due to post-enrollment use of anti-inflammatory medication. The underlying study was conducted in accordance with Good Clinical Practice guidelines, the principles of the Declaration of Helsinki, and relevant regulatory requirements. The original study was registered in ClinicalTrials.gov (NCT03851965, February 22, 2019) [10]. The UHL Institutional Review Board approved the study (IRB no. 60580, 11 Dec 2018), and we obtained written individual informed consent from each participant or next-of-kin. This work is reported according to STROCSS criteria [11].

2.2 Study objectives

The goals of the present study were (1) to characterize the relationship between Pmca and sublingual microcirculatory variables and RBC velocity; (2) to characterize the relationship between sublingual RBC velocity and O2ER; and (3) to develop CFD models using clinical data to evaluate the velocity and pressure fields in microvessels.

2.3 Patient eligibility

We considered adults fulfilling the following criteria: sinus rhythm in electrocardiogram; no evidence of structural heart disease confirmed by preoperative echocardiography; and American Society of Anesthesiologists’ (ASA) physical status I.

2.4 Anesthetic management

Before anesthesia induction, all patients received 5 mL kg-1 of a balanced crystalloid solution to compensate for preoperative fasting and vasodilation associated with general anesthesia. Anesthesia was induced in the supine position, and included midazolam 0.15-0.35 mg kg-1, fentanyl 1 μg kg-1, ketamine 0.2 mg kg-1, propofol 1.5-2 mg kg-1, rocuronium 0.6 mg kg-1, and a fraction of inspired oxygen of 0.7. After tracheal intubation, patients were mechanically ventilated using a lung-protective strategy with tidal volume of 7 mL kg-1, positive end-expiratory pressure of 6-8 cmH2O, and plateau pressure <30 cmH2O (Draeger Perseus A500®; Drägerwerk AG & Co., Lübeck, Germany).

General anesthesia was maintained by inhalation of desflurane at an initial 1.0 minimal alveolar concentration. Thereafter, depth of anesthesia was adjusted to maintain Bispectral Index (BIS, Covidien, France) between 40 and 60 [12-14]. Intraoperative fraction of inspired oxygen was then adjusted to maintain an arterial oxygen partial pressure of 80-100 mmHg and normocapnia was maintained by adjusting the respiratory rate as needed [15-17]. Normothermia (37 °C) and normoglycemia were maintained during the perioperative period.

The radial artery was cannulated and connected to a FloTrac/EV1000 clinical platform (Edwards Life Sciences, Irvine, CA, USA) to directly measure mean arterial pressure (MAP), CO and cardiac index (CI), stroke volume (SV), stroke volume variation (SVV), and systemic vascular resistance (SVR). The internal jugular vein was cannulated with a triple-lumen central venous catheter that was connected to a pressure transducer to measure central venous pressure (CVP). Before study measurements, we confirmed that transducers were correctly leveled and zeroed, while the system’s dynamic response was confirmed with fast-flush tests. Artifacts were detected and removed when documented as such and when measurements were out-of-range or systolic and diastolic pressures were similar or abruptly changed (≥40 mmHg decrease or increase within 2 min before and after measurement). Oxygen extraction ratio was calculated as the ratio of oxygen consumption (VO2) to oxygen delivery (DO2) using the formula O2ER = VO2 / DO2 = (SaO2 - ScvO2) / SaO2.

2.5 Calculation of mean circulatory filling pressure analogue and related variables

The methods of the Pmca algorithm have been described in detail before [3,18-20]. Briefly, based on a Guytonian model of the systemic circulation [CO = VR = (Pmcf − CVP) / RVR], an analogue of Pmcf can be derived using the mathematical model Pmca = (a × CVP) + (b × MAP) + (c × CO) [2,21]. In this formula, a and b are dimensionless constants (a + b = 1). Assuming a veno-arterial compliance ratio of 24:1, a = 0.96 and b = 0.04, reflecting the contribution of venous and arterial compartments, and c resembles arteriovenous resistance and is based on a formula including age, height, and weight [2]: Embedded Image In addition, the following values were determined: (1) Pressure gradient for venous return (PGVR) was defined as the pressure difference between Pmca and CVP (PGVR = Pmca – CVP); (2) Resistance to venous return (RVR) was defined as the resistance downstream of Pmca to reflect resistance for venous return and was calculated as the ratio of the pressure difference between Pmca and CVP and CO [RVR= (Pmca – CVP) / CO]. This formula is used to describe venous return during transient states of imbalances (Pmca is the average pressure in the systemic circulation and RVR is the resistance encountered to the heart) [22,23].

2.6 Sublingual microcirculation analysis

Sublingual microcirculation was monitored using SDF+ imaging (Microscan; Microvision Medical BV, Amsterdam, The Netherlands). Microcirculation was assessed 30 minutes after induction of general anesthesia before surgical incision. We recorded sublingual microcirculation videos from at least five sites. All videos were recorded by the same investigator who was blinded to systemic hemodynamic measurements. To optimize video quality, we tried to avoid pressure and movement artefacts, optimized focus and illumination, and cleaned saliva and/or blood from the sublingual mucosa.

2.7 Computational Fluid Mechanics

A numerical study was performed utilizing the CFD approach and randomly selected patient data. Randomization was achieved by using random computer-generated numbers. Systemic hemodynamic data were collected by an individual who was blinded to sublingual hemodynamic measurements. The latter were collected by another individual who was blinded to systemic hemodynamic data.

We reconstructed the 2D microvessels and applied CFD to evaluate the correlation of Pmca and RBC velocity with the obtained pressure and velocity fields in microvessels from CFD [i.e., pressure difference (Δp)] under laminar flow assuption. For the blood flow in a blood vessel, Δp is the pressure difference between any two points along its given length, discribing the main driving force of blood motion in the vessel. The discrete equations of fluid flow are the continuity and momentun (Navier-Stokes) equations. These equations form a non-linear system of Partial Differential Equations (PDEs). This system was numerically solved using the Finite Volume (FV) method for the steady state problem. The discretized algebraic system was solved using the Semi-Implicit Method for Pressure Linked Equation algorithm (SIMPLE). The method is described in detail elsewhere [24].

The laminar numerical simulations were performed in the software package Ansys Fluent (Ansys Inc., Canonsburg, PA). Blood was considered as a Newtonian fluid with density ρ = 1050 Kg m-3 and kinematic viscosity v = 3.2×10-6 m2 s-1. The numerical scheme was converged when the residuals (errors) of the momentum and continuity equations were less than or equal to the predetermined error, i.e., error =10−6, in this study. At the inlet(s), we considered a constant velocity profile obtained from the measurments of this study, specific for each patient. At the outlet(s), a pressure outlet condition was applied, meaning that the pressure at the outlet has a predifined value. Finally, a no slip condition was applied to the microvessel walls, following the rigid wall assumption. More details about the numerical approach can be found elsewhere [25].

2.8 Statistical Analysis

Before analysis, all sublingual perfusion videos were evaluated by two experienced raters blinded to all patient data, according to a modified microcirculation image quality score (MIQS) [26]. The best three videos from each recording were analysed offline by a blinded investigator with the AVA4.3C Research Software (Microvision Medical, Amsterdam, the Netherlands) [27,28]. We analysed the De Backer score and De Backer score (small) as density scores, and the Consensus Proportion of Perfused Vessels (Consensus PPV) and Consensus PPV (small) as flow scores. Vessel diameter, vessel length, and RBC velocity were determined with the latest version of AVA Software using a modified optical flow-based algorithm. The method uses per video frame data to measure the overall velocity per vessel segment.

The statistical significance of the hemodynamic variations between the variables analyzed in each microcirculation video was determined by non-parametric ANOVA tests. The studied variables are presented with their mean value (MV) and standard deviation (SD). For correlating the data, the Kendall’s rank correlation between multiple time series was utilized [29]. In this test, we conducted a hypothesis test to determine which correlations are significantly different from zero. The correlation coefficients highlighted in red indicate which pairs of variables have correlations significantly different from zero. Due to the study sample (n=20), post-hoc bootstrapping metrics were used to allow estimation of the sampling distribution using random sampling methods. The analysis, including the post-hoc bootstrapping, was performed in Matlab (MathWorks, Natick, Massachusetts, USA). P values less than 0.05 were deemed significant.

3. RESULTS

Twenty patients were included in the study, of whom 12 (60%) were men and 8 (40%) were women, with a median age of 39.5 years (IQR 35.5-44.5). Demographic and clinical characteristics are shown in Supplemental Table 1, while the anesthetic parameters 30 min after induction of anesthesia are depicted in Supplemental Table 2.

3.1 Baseline systemic and sublingual microcirculatory variables

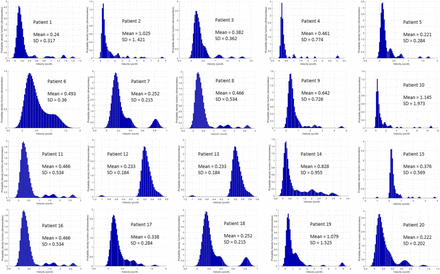
Baseline hemodynamic and metabolic parameters were within normal range (Tables 1 and 2). Mean arterial pressure was maintained ≥65 mmHg without vasopressor administration. Sublingual velocity distributions were similar and followed a log-normal distribution, but distinct differences with different mean values were observed from case to case (Figure 1). An additional statistical analysis with a non-parametric ANOVA test showed that the velocity distributions were significantly different among patients (p<0.001). The aforementioned physiological characteristics were translated into a mean DO2 and VO2 of 973.8±116.2 ml min-1 and 247.4±35.6 ml min-1, respectively.

View this table:
Table 1. Baseline systemic hemodynamic and metabolic parameters (mean value ± standard deviation)
View this table:
Table 2. Baseline values of microcirculatory variables (mean value ± standard deviation)
Figure 1.
Figure 1.

Probability density functions of the velocity distributions. Note the velocity values (mean) and the standard deviation (SD).

3.2 Correlation of Pmca with systemic and microcirculatory variables

The correlation of Pmca with systemic hemodynamic variables and sublingual microcirculatory flow and density variables is depicted in Table 3.

View this table:
Table 3. Correlation of Pmca with systemic hemodynamic variables and sublingual flow and density variables

3.3 Correlation of Pmca with sublingual RBC velocity and microvessel length

A negative correlation was observed between Pmca and RBC velocity (r=-0.03, p=0.87). Interestingly, a constant Pmca value of 14 mmHg was observed in all individuals with sublingual RBC velocity of 6-24 μm s-1. On the contrary, a Pmca <14 mmHg was observed in those with RBC velocity >24 μm s-1 (Figure 2). In addition, a positive correlation between Pmca and sublingual microvessel length was also observed (r=0.04, p=0.82; Supplementary Figure 1).

Figure 2.
Figure 2.

Correlation of Pmca with sublingual RBC velocity in individuals with steady-state physiology, effective coupling between the macro- and microcirculation, and normal tissue oxygen extraction ratio. A constant Pmca of 14 mmHg was observed in individuals with RBC velocity of 6-24 μm/s, while a Pmca of <14 mmHg was observed in those with RBC velocity >24 μm/s.

Pmca, mean circulatory filling pressure analogue; RBC, red blood cell.

3.4 Correlation of sublingual RBC velocity with microvessel diameter and length

A negative correlation between RBC velocity and microvessel length (r=-0.19, p=0.27) was observed in all patients. Additionally, a positive correlation was observed between RBC velocity and microvessel diameter (r=0.68, p<0.001; Supplementary Figure 2).

3.5 Correlation of sublingual RBC velocity with density and flow variables and O2ER

A positive correlation was observed between RBC velocity and De Backer score (r=0.2, p=0.24), De Backer score (small) (r=0.26, p=0.125), and Consensus PPV (small) (r=0.07, p=0.73) (Supplementary Table 3, Supplementary Figure 3). Also, a positive correlation was observed between mean RBC velocity and O2ER (r=0.034, p=0.87).

3.6 Computational Fluid Mechanics

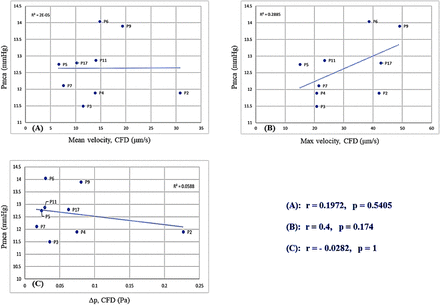
Reconstruction of the 2D microvessel and application of CFD to evaluate the velocity and pressure fields in microvessels are depicted in Supplementary Figures 4-12. Correlation of Pmca with RBC velocity and pressure drop (Δp) is depicted in Figure 3. Interestingly, when Pmca ranged between 11 mmHg and 15 mmHg, Δp fluctuated between 0.02 Pa and 0.1 Pa. Bootstrapping metrics (n=30) revealed a statistically significant negative correlation between Pmca and Δp (r=-0.30, p=0.02) (Supplementary Figure 13).

Figure 3.
Figure 3.

Computational fluid dynamics simulation: (A) Correlation between Pmca and mean RBC velocity; (B) Correlation between Pmca and maximum velocity in the domain; (C) Correlation between Pmca and pressure difference (Δp).

4. DISCUSSION

In this explorative study with anesthetized individuals in steady-state physiology, a constant Pmca value of 14 mmHg was observed in those with sublingual RBC velocity of 6-24 μm s-1, while a Pmca <14 mmHg was observed in those with RBC velocity >24 μm s-1. A positive correlation was observed between RBC velocity and O2ER. In addition, CFD modeling simulation revealed a negative correlation between Pmca και Δp. When Pmca ranged between 11 mmHg and 15 mmHg, Δp constantly fluctuated between 0.02 Pa and 0.1 Pa. The present study provides a novel method to monitor hemodynamic coherence and tissue perfusion, which can aid in the identification of novel hemodynamic phenotypes and enhance microcirculation-guided therapeutic strategies, optimizing local delivery of oxygen.

An intact coherence between the macro- and microcirculation facilitates DO2 to the parenchymal cells. Patients undergoing general anesthesia and critically ill patients may experience a transient or prolonged loss of this coherence, which may lead to tissue hypoperfusion and organ injury. Although the expansion of hemodynamic monitoring to include monitoring of the microcirculation may be helpful in guiding management [30], its visualization and assessment remains technically challenging. Therefore, identifying potential systemic hemodynamic variables that would enable prediction of microcirculatory behavior is of highest interest [31]. In this clinical study with CFD analysis, we report that a Pmca of 14 mmHg is associated with physiological hemodynamic coherence, effective microcirculatory perfusion, and oxygen transport to tissue. As hemodynamic reference values or thresholds are needed to define microcirculatory alterations as persisting, Pmca may prove an indirect assessment method of tissue perfusion, allowing microcirculation-guided resuscitation and aiding in the identification of novel hemodynamic phenotypes [5,28].

In normal conditions, organ perfusion is dependent upon CO and the vascular resistance across an organ, while in circulatory shock, fluid resuscitation is often necessary to achieve maximal tissue RBC perfusion [32]. The present study included individuals with steady-state physiology, intact vascular regulation, and effective coupling between the macro- and microcirculation, which allowed the description of their functional state. Of note, the association between systemic hemodynamic and microcirculatory variables may still exist when hemodynamic coherence is lost [31]. This is important for the monitoring and treatment of hemodynamic abnormalities, especially in the early phase of diseases during which hemodynamic coherence is usually maintained [31]. In our patients with dynamic hemodynamic equilibrium, a lower Pmca value (<14 mmHg) was correlated with higher RBC velocity, probably due to an increase in vascular capacitance and sublingual vessel diameter and/or CO. However, there must be always a limit under which decreases in Pmca and venous return impair microcirculatory blood flow [5,33]. On the contrary, a higher Pmca may be the result of excessive vasoconstriction, eventually resulting in hemodynamic incoherence and tissue hypoperfusion. These may explain the detrimental effects of higher doses of adrenergic vasoconstrictive agents and support the recent trend towards a perfusion-centered resuscitation strategy instead of standard pressure-guided treatment [34,35].

In the present study, mean RBC velocity was 15±9 μm s-1, which is significantly lower compared to this reported in other studies including healthy individuals. Edul et al. reported a normal RBC velocity of 1331±90 μm s-1 [8,9], while Rovas et al. recently reported a normal RBC velocity of approximately 102 μm s-1 [36]. Nevertheless, the available evidence is not sufficient to rule out different RBC velocities in healthy people [37]. The lower RBC velocity in our patients is suggestive of a hypodynamic microcirculatory state, with the normal O2ER indicating a physiological balance between DO2 and VO2. This, together with the microcirculatory density and flow scores in the present study, strengthen the evidence revealing that tissue oxygenation can be maintained in very low RBC velocities. Theoretically, oxygen transport to tissue is facilitated when RBC velocity is low, while tissue hypoxia may develop when RBC velocity increases because the capillary transit time of the RBCs may not be sufficient to unload oxygen completely [6,8]. However, whether a hyperdynamic microcirculatory flow is always associated with tissue hypoxia remains controversial. In septic patients, individual changes in sublingual RBC velocity have been correlated with those in cardiac index after a fluid bolus, but in the face of an unchanged perfused vascular density [9]. In others, a fluid challenge may improve O2ER by increasing Pmcf and venous return [38]. The aforementioned data and the findings of the present study encourage further translational research aimed at the elucidation of their broader implications.

The application of CFD simulations revealed a negative correlation between Pmca και Δp. For the blood flow in a vessel or organ, Δp is the pressure difference between any two points along a given length of the vessel or the difference between the arterial and venous pressures, respectively. In our CFD analysis with laminar flow conditions, with the vascular resistance being independent of flow and pressure, an increase in resistance would decrease flow at any given Δp. In clinical practice, a fluid challenge may increase the stressed volume (and thus Pmca and CO) until a certain point, but may not always improve microcirculatory perfusion. On the other hand, fluid overload increases CVP, which decreases venous return and retrogradely increases post-capillary venular pressure, impairing microcirculatory perfusion [39-41]. The association between the Pmca and Δp ranges in our study (Figure 3) further enhances the potential of Pmca to serve as a hemodynamic coherence monitoring tool. Bedside estimation of Pmca can track the effective circulatory blood volume and a constant value of 14 mmHg may ensure an adequate balance between macrocirculatory pressure and microcirculatory perfusion [42,43]. The post-hoc bootstrapping metrics in the present study strongly encourage the evaluation of our findings in larger studies.

To the best of our knowledge, this is the first report of the association between Pmcf/Pmca and sublingual RBC velocity and Δp. Another strength is that data analyses were performed by blinded investigators, thus preventing inter-observer bias and increasing the credibility of study conclusions. Although the present study includes a small patient sample, bootstrapping metrics revealed a statistically significant negative correlation between Pmca and Δp. Mean age in our patients was 39.5 years and the results of the present analysis may be different in older individuals. In addition, anesthesia can lower resting metabolic rate and reduce global VO2, and has been associated with a reduction in tissues ability to extract oxygen. In the present study, however, we used desflurane for maintenance because it produces mild and stable effects on the microcirculation compared to other agents [12].

5. CONCLUSIONS

The intact regulatory mechanisms may maintain a physiological coupling between systemic hemodynamics and tissue perfusion and oxygenation when Pmca is 14 mmHg, indicating its potential to serve as a marker of hemodynamic coherence.

Data Availability

Data can be made available upon request after publication through a collaborative process. Researchers should provide a methodically sound proposal with specific objectives in an approval proposal. Please contact the corresponding author for additional information.

Declarations of interest

None.

Sources of Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Authors’ contributions

Conceptualization: AC. Data curation: AC, MX. Formal analysis: AC, MX. Methodology: AC, MX. Project administration: AC. Visualization: AC, MX. Writing - original draft: AC. Writing - review & editing: AC, MX.

Data Sharing Statement

Data can be made available upon request after publication through a collaborative process. Researchers should provide a methodically sound proposal with specific objectives in an approval proposal. Please contact the corresponding author for additional information.

Acknowledgements

This research was partially supported by the Hellenic Society of Cardiopulmonary Resuscitation, Athens, Greece. The authors would like to thank the medical and nursing stuff of the Department of Anesthesiology of the University Hospital of Larisa, Greece, for their assistance during the study period. We are also thankful to Z. Hossain, medical software engineer at Microvision Medical (Amsterdam, The Netherlands), who provided expertise that greatly assisted the research.

REFERENCES

  1. [1].↵
    de Keijzer IN, Scheeren TWL. Perioperative Hemodynamic Monitoring: An Overview of Current Methods. Anesthesiol Clin 2021;39:441–56. doi: 10.1016/j.anclin.2021.03.007.
    OpenUrlCrossRef
  2. [2].↵
    Wijnberge M, Sindhunata DP, Pinsky MR, et al. Estimating mean circulatory filling pressure in clinical practice: a systematic review comparing three bedside methods in the critically ill. Ann Intensive Care 2018;8:73. doi: 10.1186/s13613-018-0418-2.
    OpenUrlCrossRef
  3. [3].↵
    Parkin G, Wright C, Bellomo R, Boyce N. Use of a mean systemic filling pressure analogue during the closed-loop control of fluid replacement in continuous hemodiafiltration. J Crit Care 1994;9:124–33. doi: 10.1016/0883-9441(94)90023-x.
    OpenUrlCrossRefPubMedWeb of Science
  4. [4].↵
    Henderson WR, Griesdale DE, Walley KR, Sheel AW. Clinical review: Guyton--the role of mean circulatory filling pressure and right atrial pressure in controlling cardiac output. Crit Care 2010;14:243. doi: 10.1186/cc9247.
    OpenUrlCrossRefPubMed
  5. [5].↵
    Vos JJ, Kalmar AF, Scheeren TWL. Bedside assessment and clinical utility of mean systemic filling pressure in acute care. J Emerg Crit Care Med 2020;4:25. doi: 10.21037/jeccm.2020.03.04.
    OpenUrlCrossRef
  6. [6].↵
    Gutierrez G. The rate of oxygen release and its effect on capillary O2tension: a mathematical analysis. Respir Physiol 1986;63:79–96. doi: 10.1016/0034-5687(86)90032-0.
    OpenUrlCrossRefPubMedWeb of Science
  7. [7].↵
    Dubin A, Kanoore Edul VS, Caminos Eguillor JF, Ferrara G. Monitoring Microcirculation: Utility and Barriers -A Point-of-View Review. Vasc Health Risk Manag 2020;16:577–89. doi: 10.2147/VHRM.S242635.
    OpenUrlCrossRef
  8. [8].↵
    Edul VS, Enrico C, Laviolle B, Vazquez AR, Ince C, Dubin A. Quantitative assessment of the microcirculation in healthy volunteers and in patients with septic shock. Crit Care Med 2012;40:1443–8. doi: 10.1097/CCM.0b013e31823dae59.
    OpenUrlCrossRefPubMedWeb of Science
  9. [9].↵
    Edul VS, Ince C, Navarro N, et al. Dissociation between sublingual and gut microcirculation in the response to a fluid challenge in postoperative patients with abdominal sepsis. Ann Intensive Care 2014;4:39. doi: 10.1186/s13613-014-0039-3.
    OpenUrlCrossRefPubMed
  10. [10].↵
    Chalkias A, Laou E, Kolonia K, et al. Elevated preoperative suPAR is a strong and independent risk marker for postoperative complications in patients undergoing major noncardiac surgery (SPARSE). Surgery 2021. In press. doi: 10.1016/j.surg.2021.10.012.
    OpenUrlCrossRef
  11. [11].↵
    Agha R, Abdall-Razak A, Crossley E, Dowlut N, Iosifidis C, Mathew G; STROCSS Group. STROCSS 2019 Guideline: Strengthening the reporting of cohort studies in surgery. Int J Surg 2019;72:156–65. doi: 10.1016/j.ijsu.2019.11.002.
    OpenUrlCrossRef
  12. [12].↵
    Özarslan NG, Ayhan B, Kanbak M, et al. Comparison of the effects of sevoflurane, isoflurane, and desflurane on microcirculation in coronary artery bypass graft surgery. J Cardiothorac Vasc Anesth 2012;26:791–8. doi: 10.1053/j.jvca.2012.03.019.
    OpenUrlCrossRefPubMed
  13. [13].
    Kertai MD, White WD, Gan TJ. Cumulative duration of “triple low” state of low blood pressure, low bispectral index, and low minimum alveolar concentration of volatile anesthesia is not associated with increased mortality. Anesthesiology 2014;121:18–28. doi: 10.1097/ALN.0000000000000281.
    OpenUrlCrossRef
  14. [14].↵
    Willingham M, Ben Abdallah A, Gradwohl S, et al. Association between intraoperative electroencephalographic suppression and postoperative mortality. Br J Anaesth 2014;113:1001–8. doi: 10.1093/bja/aeu105.
    OpenUrlCrossRefPubMed
  15. [15].↵
    Milstein DM, Helmers R, Hackmann S, Belterman CN, van Hulst RA, de Lange J. Sublingual microvascular perfusion is altered during normobaric and hyperbaric hyperoxia. Microvasc Res 2016;105:93–102. doi: 10.1016/j.mvr.2016.02.001.
    OpenUrlCrossRef
  16. [16].
    Schwarte LA, Schober P, Loer SA. Benefits and harms of increased inspiratory oxygen concentrations. Curr Opin Anaesthesiol 2019;32:783–91. doi: 10.1097/ACO.0000000000000791.
    OpenUrlCrossRef
  17. [17].↵
    Orbegozo Cortés D, Puflea F, Donadello K, et al. Normobaric hyperoxia alters the microcirculation in healthy volunteers. Microvasc Res 2015;98:23–8. doi: 10.1016/j.mvr.2014.11.006.
    OpenUrlCrossRefPubMed
  18. [18].↵
    Parkin WG. Volume state control - a new approach. Crit Care Resusc 1999;1:311–21.
    OpenUrlPubMed
  19. [19].
    Parkin WG, Leaning MS. Therapeutic control of the circulation. J Clin Monit Comput 2008;22:391–400. doi: 10.1007/s10877-008-9147-7.
    OpenUrlCrossRefPubMed
  20. [20].↵
    Pellegrino VA, Mudaliar Y, Gopalakrishnan M, et al. Computer based haemodynamic guidance system is effective and safe in management of postoperative cardiac surgery patients. Anaesth Intensive Care 2011;39:191–201. doi: 10.1177/0310057X1103900207.
    OpenUrlCrossRefPubMedWeb of Science
  21. [21].↵
    Meijs LPB, van Houte J, Conjaerts BCM, Bindels AJGH, Bouwman A, Houterman S, Bakker J. Clinical validation of a computerized algorithm to determine mean systemic filling pressure. J Clin Monit Comput 2022;36:191–98. doi: 10.1007/s10877-020-00636-2.
    OpenUrlCrossRef
  22. [22].↵
    Berger D, Moller PW, Takala J. Reply to “Letter to the editor: Why persist in the fallacy that mean systemic pressure drives venous return?”. Am J Physiol Heart Circ Physiol 2016;311:H1336–7. doi: 10.1152/ajpheart.00622.2016.
    OpenUrlCrossRefPubMed
  23. [23].↵
    Berger D, Moller PW, Weber A, et al. Effect of PEEP, blood volume, and inspiratory hold maneuvers on venous return. Am J Physiol Heart Circ Physiol 2016;311:H794–806. doi: 10.1152/ajpheart.00931.2015.
    OpenUrlCrossRefPubMed
  24. [24].↵
    Patankar SV. Numerical Heat Transfer and Fluid Flow. 1st ed. Boca Raton: CRC Press, 1980.
  25. [25].↵
    Georgakarakos E, Ioannidis G, Raptis A, Xenos M. Computational Fluid Dynamic Analysis Supports the Hemodynamic Stability of Hybrid Combinations With the AFX Bifurcate and Nitinol-Based Proximal Segments in Solutions of Failed Endovascular Aneurysm Repair. Vasc Endovascular Surg 2021;55:907–9. doi: 10.1177/15385744211037490.
    OpenUrlCrossRef
  26. [26].↵
    Massey MJ, Larochelle E, Najarro G, et al. The microcirculation image quality score: development and preliminary evaluation of a proposed approach to grading quality of image acquisition for bedside videomicroscopy. J Crit Care 2013;28:913–7. doi: 10.1016/j.jcrc.2013.06.015.
    OpenUrlCrossRefPubMed
  27. [27].↵
    Dobbe JG, Streekstra GJ, Atasever B, van Zijderveld R, Ince C. Measurement of functional microcirculatory geometry and velocity distributions using automated image analysis. Med Biol Eng Comput 2008;46:659–70. doi: 10.1007/s11517-008-0349-4.
    OpenUrlCrossRefPubMedWeb of Science
  28. [28].↵
    Ince C, Boerma EC, Cecconi M, et al; Cardiovascular Dynamics Section of the ESICM. Second consensus on the assessment of sublingual microcirculation in critically ill patients: results from a task force of the European Society of Intensive Care Medicine. Intensive Care Med 2018;44:281–99. doi: 10.1007/s00134-018-5070-7.
    OpenUrlCrossRefPubMed
  29. [29].↵
    Kendall MG. Rank Correlation Methods. 3rd ed. New York: Hafner Publishing Company, 1962.
  30. [30].↵
    Weil MH, Tang W. Welcoming a new era of hemodynamic monitoring: expanding from the macro to the microcirculation. Crit Care Med 2007;35:1204–5. doi: 10.1097/01.CCM.0000259169.33624.D2.
    OpenUrlCrossRefPubMed
  31. [31].↵
    Behem CR, Graessler MF, Friedheim T, Kluttig R, Pinnschmidt HO, Duprée A. The use of pulse pressure variation for predicting impairment of microcirculatory blood flow. Sci Rep 2021;11:9215. doi: 10.1038/s41598-021-88458-3.
    OpenUrlCrossRef
  32. [32].↵
    Hilty MP, Ince C. Automated quantification of tissue red blood cell perfusion as a new resuscitation target. Curr Opin Crit Care 2020;26:273–80. doi: 10.1097/MCC.0000000000000725.
    OpenUrlCrossRef
  33. [33].↵
    Bouattour K, Teboul JL, Varin L, Vicaut E, Duranteau J. Preload Dependence Is Associated with Reduced Sublingual Microcirculation during Major Abdominal Surgery. Anesthesiology 2019;130:541–9. doi: 10.1097/ALN.0000000000002631.
    OpenUrlCrossRef
  34. [34].↵
    Gazmuri RJ, de Gomez CA. From a pressure-guided to a perfusion-centered resuscitation strategy in septic shock: Critical literature review and illustrative case. J Crit Care 2020;56:294–304. doi: 10.1016/j.jcrc.2019.11.008.
    OpenUrlCrossRef
  35. [35].↵
    De Backer D, Foulon P. Minimizing catecholamines and optimizing perfusion. Crit Care 2019;23:149. doi: 10.1186/s13054-019-2433-6.
    OpenUrlCrossRef
  36. [36].↵
    Rovas A, Sackarnd J, Rossaint J, Kampmeier S, Pavenstädt H, Vink H. Identification of novel sublingual parameters to analyze and diagnose microvascular dysfunction in sepsis: the NOSTRADAMUS study. Crit Care 2021;25:112. doi: 10.1186/s13054-021-03520-w.
    OpenUrlCrossRef
  37. [37].↵
    Edul VS, Ince C, Vazquez AR, Rubatto PN, Espinoza ED, Welsh S. Similar Microcirculatory Alterations in Patients with Normodynamic and Hyperdynamic Septic Shock. Ann Am Thorac Soc 2016;13:240–7. doi: 10.1513/AnnalsATS.201509-606OC.
    OpenUrlCrossRef
  38. [38].↵
    Bennett VA, Vidouris A, Cecconi M. Effects of Fluids on the Macro-and Microcirculations. Crit Care 2018;22:74. doi: 10.1186/s13054-018-1993-1.
    OpenUrlCrossRef
  39. [39].↵
    Chalkias A, Papagiannakis N, Mavrovounis G, Kolonia K, Mermiri M, Pantazopoulos I, Laou E, Arnaoutoglou E. Sublingual microcirculatory alterations during the immediate and early postoperative period: A systematic review and meta-analysis. Clin Hemorheol Microcirc 2022;80:253–65. doi: 10.3233/CH-211214.
    OpenUrlCrossRef
  40. [40].
    Chalkias A, Xanthos T, Papageorgiou E, Anania A, Beloukas A, Pavlopoulos F. Intraoperative initiation of a modified ARDSNet protocol increases survival of septic patients with severe acute respiratory distress syndrome. Heart Lung 2018;47:616–21. doi: 10.1016/j.hrtlng.2018.06.011.
    OpenUrlCrossRef
  41. [41].↵
    Suker M, Tovar Doncel MS, Pinto Lima AA, Ince C, van Eijck Chj. Sublingual microcirculation in pancreatico-biliary surgery: An observational study. Clin Hemorheol Microcirc 2019;72:247–57. doi: 10.3233/CH-180448.
    OpenUrlCrossRef
  42. [42].↵
    Maas JJ, Pinsky MR, Geerts BF, de Wilde RB, Jansen JR. Estimation of mean systemic filling pressure in postoperative cardiac surgery patients with three methods. Intensive Care Med 2012;38:1452–60. doi: 10.1007/s00134-012-2586-0.
    OpenUrlCrossRefPubMed
  43. [43].↵
    Werner-Moller P, Sondergaard S, Jakob SM, Takala J, Berger D. Effect of volume status on the estimation of mean systemic filling pressure. J Appl Physiol (1985) 2019;126:1503–13. doi: 10.1152/japplphysiol.00897.2018.
    OpenUrlCrossRef
Back to top
Posted May 10, 2022.
Download PDF

Supplementary Material

Data/Code
Email
Association of effective circulating blood volume with sublingual RBC velocity and microvessel pressure difference in anesthetized individuals: A clinical investigation and computational fluid dynamics modeling
Athanasios Chalkias, Michalis Xenos
medRxiv 2022.05.09.22274826; doi: https://doi.org/10.1101/2022.05.09.22274826
Twitter logo Facebook logo LinkedIn logo Mendeley logo
Citation Tools

Subject Area