Abstract
In late 2020, the JCVI (the Joint Committee on Vaccination and Immunisation, which provides advice to the Department of Health and Social Care, England) made two important recommen-dations for the initial roll-out of the COVID-19 vaccine. The first was that vaccines should be targeted to the elderly and vulnerable, with the aim of maximally preventing disease rather than infection - a prioritisation that has become the adopted practice in many countries. The second was to increase the interval between first and second doses for 3 to 12-weeks, which both accounted for the observation that the ChAdOx vaccine appeared to have a higher efficacy with this longer dose interval, and that by delaying second doses the capacity to deliver first doses was increased. Here, using the latest data on vaccine efficacy we re-examine these recommendations through a mathematical model, to understand their short and medium-term impacts in England. In particular, we show that targeting the most vulnerable had the biggest immediate impact (compared to targeting younger individuals who may be more responsible for transmission). The 12-week delay was also highly beneficial, estimated to have averted between 32-72 thousand hospital admissions and 4-9 thousand deaths over the first ten months of the campaign (December 2020 - September 2021) - depending on the assumed interaction between dose interval and efficacy.
Without doubt, the development of vaccines has been one of the greatest breakthroughs reducing the scale and impact of the on-going SARS-CoV-2 pandemic. Since their deployment in late 2020 and early 2021, they have had a profound impact on the levels of infection and disease globally, and have allowed many countries to relax mitigation measures. Vaccines need to be deployed effectively to maximise their public health benefit; this requires detailed epidemiological input from a variety of sources, often extrapolated through mathematical projections. However, decisions need to be made rapidly to have the maximal benefit, usually before all the evidence can be systematically gathered and collated.
The UK was the first country to begin their vaccine deployment campaign, rapidly followed by Israel, the U.S.A. and European nations [1]. One of the earliest decisions was to target vaccination at the most vulnerable groups (to generate the maximal impact on severe disease) and healthcare workers (to maintain a functioning healthcare system) [2]. An alternative prioritisation programme may instead have sought to reduce infection as quickly as possible [3], by vaccinating the younger generations that were driving transmission. The general question as to when vaccination should be targeted at individuals generating the most transmission and when it should be targeted at the vulnerable remains an open problem (and is likely to depend on population demographics, vaccine characteristics and the heterogeneity in transmission risk and disease severity); but in late 2020 with an absence of data on whether the vaccine would reduce transmission, the decision to vaccinate the elderly and vulnerable first was relatively clear cut [4]. Most other countries adopted a similar targeted approach, although there were subtle differences in the prioritising of particular vulnerabilities, age-groups and at-risk professions. For example, the UK’s first four priority groups were: care home residents and workers; those over 80 and health/social care workers; those over 75; those over 70 or clinically extremely vulnerable [2] - which was in very close agreement with the first two priority groups in Germany [5]. The French priority order was similarly age-structured (care home residents and care home workers over 50; care-givers over 50 and firefighters; those over 75 years old; those age 65-74; those age 50-64 together with those with co-morbidities, essential sector workers and those with contact with the public [6]) as was the order in the USA (health care workers and long-term care facility residents; persons aged over 75 years and front-line essential workers; persons aged 65–74 years, persons aged 16–64 years with high-risk medical conditions, and any essential workers not included in the initial phases [7]).
Related to the idea of offering maximal early protection to the elderly and vulnerable was the question of whether to prioritise first or second doses. At the time, both vaccine supply and deployment capacity were limited, and the UK was experiencing another surge in cases due to the Alpha variant[8], so making maximal use of available resources was key. Essentially the question can be conceptualised as whether it is better to provide maximal two-dose protection to a smaller number of the most vulnerable first, or whether to prioritise lower one-dose protection to a greater number of individuals [9]. For example, using population sizes from England, is it better to give two doses and hence 80% protection to the ∼500,000 people over 90 years of age or one dose and therefore 50% protection to the ∼1,000,000 people over 87; for real-world decisions this caricature is made more complex by different degrees of vulnerability and changing vaccination capacity (which was generally increasing throughout the early phase following initial roll-out). In addition, evidence was emerging that the AstraZeneca ChAdOx1 vaccine, which was the main early component of the UK programme, had better efficacy if the interval between doses was extended from 3 to 12 weeks [10]. The decision was therefore made in the UK to adopt a 12-week dose interval for all UK vaccines [11], allowing the first three months of the programme to be dedicated to giving as many people as possible the protection offered by one dose of the vaccine. Very few countries followed this example; most including the USA and the majority of countries in Europe opted for a 3-4 week interval [12, 13] although Canada instigated a 16 week interval [14]. (We note that in May 2021, to combat the rise in hospital admissions, the dose interval in the UK was shortened to 8-weeks [15], in response to concerns about the degree of protection from one dose against the Delta variant and to ensure two-dose protection in more vulnerable groups.)
Here we use mathematical models, developed and matched to epidemic data from England throughout the pandemic (see Supplementary Material), to retrospectively assess the implications of the vaccine dose separation and prioritisation decisions by simulating counterfactual scenarios. We consider four different scenarios: (i) the default model, which has been fitted to the epidemiological data (community cases, hospital admissions, hospital occupancy and deaths, from the start of the pandemic until June 2022), playing back the recorded vaccination times (corresponding to 12-week and then 8-week intervals); (ii) a model in which the vaccination order is reversed, but the interval is fixed at 12-weeks, such that the youngest adults, most responsible for transmission, are vaccinated first; (iii) a model in which the order of receiving the first dose is preserved but second doses are given after a 3-week interval, with all efficacy parameters the same as with the 12-week interval; and finally (iv) a model with a 3-week dose interval that captures the vaccine efficacy differences of a shorter dose interval. In all four scenarios, the number of doses administered each day remains as observed, as does the finally attained uptake within each age-group. We consider hospital admissions and deaths from December 2020 (when the vaccine campaign began) to September 2021 (when booster doses started), and assume that all other policy decisions (such as the steps taken as part of the Roadmap out of lockdown [16]) and population behaviour are unaffected by the scenario chosen.
To account for the vaccine efficacy differences arising from a shorter interval, we rely on the analyses of Khoury [17], which links the level of neutralising antibodies to the degree of vaccine protection, and the experimental work of the Com-COV (Comparing COVID-19 Vaccine Schedule Combinations) group [18], which measured neutralising antibodies for 4 and 12 week dose intervals. Comparing a 4-week interval to the longer 12-week interval [18] reports a 2.35 (1.75-3.16) reduction in pseudotyped virus neutralised antibody level for two doses of the AstraZeneca ChAdOx1 vaccine, and a 1.44 (1.14-1.81) reduction for two doses of the Pfizer BNT162b2 vaccine. Using the relationship in [17], these lower neutralisation results for the shorter interval can be used to determine the vaccine efficacy against symptomatic infection following a second dose. Against the Alpha variant, the ChAdOx1 efficacy is reduced from 80% to 66% while the BNT162b2 efficacy is reduced for from 88% to 82%; similar reductions from 70% to 49% and 90% to 85% are obtained against Delta variant. Given the lack of evidence, we assume that efficacy against severe disease (hospital admission or death) and the rate of waning protection is unaffected by the dose interval; as such, our results are possibly a best-case scenario.
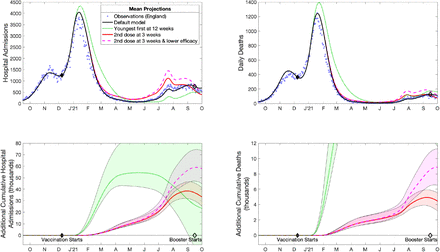
Our results show that the policy of vaccinating the oldest (and most vulnerable) first (Fig.1a,b black line) led to a faster decline in hospital admissions and deaths than targeting the younger age groups that are more responsible for transmission (Fig.1a,b green line). However, a youngest first policy leads to lower hospital admissions (but not deaths) during the Delta wave (after July 2021) due to greater immunity in some of the elderly age groups that will have only recently been vaccinated and so protection will not have waned. There are fewer early differences when keeping the prioritisation order but reducing the dose interval (Fig.1 red and dashed pink lines), but there is still a cumulative net benefit of the default scenario (Fig.1c,d). In particular, by September 2021, a 3-week dose interval is predicted to lead to 38,400 (95% prediction intervals (PI): 31,900-46,600) more hospital admissions (Fig.1c) and 4,600 (95% PI: 3,700-5,500) more deaths (Fig.1d) than with the observed intervals. These adverse effects increase to 56,600 (95% PI: 45,800-71,500) additional hospital admissions and 7,400 (95% PI: 5,600-9,400) deaths when assuming the lower efficacy against infection associated with a 3-week interval; values would be even higher if we had assumed that the efficacy against severe disease was reduced by the shorter interval (Table 1). This echoes other model-based finding for European countries [19, 20] although here we use a model that more robustly captures the temporal dynamics.
Projected changes in hospital admissions (a, c) and deaths (b,d) with differing vaccination patterns. (a, b) Compares the observed levels of severe outcomes (hospital admission or death, blue dots) with the default model projection using the recorded pattern of vaccination (black solid line) and alternative models where this pattern is perturbed: green dotted line, the ordering of vaccination is reversed so that younger adults are vaccinated first; red solid line, vaccinations are given 3 weeks apart although the total number of daily doses administered is unaltered; pink dashed line, the same 3-week strategy as the red line, but accounting for lower efficacy from the shorter dose interval. (c, d) The cumulative additional hospital admissions (c) and deaths (d) projected from alternative assumptions, showing 95% prediction intervals (shaded regions) as well as mean values (lines). All results are from model simulations using 400 samples from the parameter posterior distributions.
Hospital admissions and deaths in England from 8th December 2020 to 1st September 2021, as observed (top row) and from four model scenarios - giving the mean and 95% prediction intervals. It should be stressed that all model results assume the same relaxation of control measures throughout 2021. All model results are from 400 samples of the posterior distribution.
While these results are compelling, there are some limitations to the method. Conceptually, we have assumed that the same behavioural changes (including population precautionary behaviour and age-dependent vaccine uptake) and legal changes (such as the relaxation steps out of lockdown) would occur irrespective of the vaccination scenario; this is unlikely to be true as the higher number of hospital admissions and deaths observed in some scenarios (especially if vaccinating younger individuals first) would likely shift the relaxation of restrictions and illicit a greater precautionary reaction from the general public[16]. Our model is age-structured and parameterised to fit the observed epidemic, but does not partition the population by other risk factors (primarily because most of the epidemiological data is not partitioned by risk). Therefore, the model cannot fully capture the prioritisation of vulnerable risk groups, especially when these are in younger ages. Longer-term dynamics, beyond September 2021 and the start of the booster programme, become more difficult to predict and would be contingent on assumptions about how the boosters were deployed and the immune landscape which is more likely driven by infection rather than vaccination in the non-default scenarios.
With the advantage of hindsight, the JCVI’s decision to prioritise first doses of SARS-CoV-2 vaccine to as many elderly or vulnerable individuals as possible early in 2021 appears to have been extremely well judged and has substantially reduced the public health burden of severe COVID-19 in England. These finding are likely to transfer to other countries with similar age-profiles and age-structured mixing. In general, we would also expect such results to hold for future pandemics whenever first doses generate substantial protection against severe disease in the most vulnerable, but bespoke models matched to available data are needed to assess the benefits on a case-by-case basis.
Data Availability
Data on cases were obtained from the COVID-19 Hospitalisation in England Surveillance System (CHESS) data set that collects detailed data on patients infected with COVID-19. Data on COVID-19 deaths were obtained from Public Health England. These raw data contain confidential information, with public data deposition non-permissible for privacy reasons. The CHESS data resides with the National Health Service (www.nhs.gov.uk) whilst the death data are available from Public Health England (www.phe.gov.uk). Again these raw data contain confidential information, with public data deposition non-permissible for privacy reasons. The ethics of the use of these data for these purposes was agreed by Public Health England with the Governments SPI-M-O / SAGE committees. Processed data (which is more aggregated) is freely available from the UK Coronavirus dashboard: https://coronavirus.data.gov.uk/
Code Availability
Specific code relating to this paper will be available shortly. Generic code used to model COVID-19 in England is available at: https://github.com/MattKeeling/RelaxationRoadmaps.git
Ethical Considerations
Data from the CHESS and SARI databases were supplied after anonymisation under strict data protection protocols agreed between the University of Warwick and Public Health England. The ethics of the use of these data for these purposes was agreed by Public Health England with the Government’s SPI-M-O / SAGE committees.
Author Contributions
M.J.K: Conceptualisation, Data curation, Formal analysis, Funding acquisition, Methodology, Software, Validation, Visualisation, Writing—Original draft, Writing—Review and Editing. L.D.: Conceptualisation, Data curation, Funding acquisition, Methodology, Software, Validation, Writing—Review and Editing. M.J.T.: Conceptualisation, Funding acquisition, Writing—Review and Editing. E.H.: Conceptualisation, Data curation, Methodology, Software, Validation, Writing—Review and Editing. S.M. Conceptualisation, Data curation, Formal analysis, Methodology, Software, Validation, Visualisation, Writing—Review and Editing.
Competing interests
All authors declare that they have no competing interests.
Supplementary Methods
Here we detail the underlying mathematical framework that defines the transmission model. We break the model description into multiple sections that combine to generate a picture of SARS-CoV-2 transmission and COVID-19 disease burden in England, with the model structure having also been detailed in previous publications [1–4].
Model overview
We built the model around the traditional deterministic SEIR (Susceptible, Exposed, Infectious, Recovered) model framework [5], with three exposed classes to capture the distribution of times from infection to becoming infectious [6], and splitting the infectious group into symptomatic and asymptomatic infection [1]. To this simple model we add additional structure to capture the effects of restricted social interaction whilst maintaining household transmission [1], and this fundamental model is then ‘replicated’ twenty-one times to mimic five-year age-groups (0 − 4, 5 − 9, …, 100+), and a further seven times to capture the different dynamics in the seven NHS regions in England. The model is written as a large number of ODEs (ordinary differential equations).
This basic model was sufficient for the early waves of infection (from January to November 2020), comprising a single variant and without vaccination. During this early phase of the pandemic, the main driving parameter was the level of precautionary behaviour, which determined the level of socialmixing and therefore the scale of transmission outside the household [7], although we also fitted a number of other parameters (including case:hospitalisation and case:mortality ratios, age-dependent effects and the relative strength of asymptomatic compared to symptomatic transmission). From the age-structured symptomatic class, we calculate the number of severe health episode outcomes (hospital admissions, intensive care unit admissions and deaths), which are both key public health observables and measures of concern for this pandemic, although these quantities do not impact the transmission dynamics (Fig.S1). We performed the fitting in a Bayesian framework, matching the data on the daily hospital admissions, hospital occupancy, ICU occupancy, deaths and proportion of community (Pillar 2) tests that are positive in each of the seven National Health Service (NHS) regions of England to a Poisson distribution with a mean given by the ODE model.
From late 2020, variants and vaccination increased the dimensionality of this model. Each new variant required a duplicate of all the infected model classes to capture differences in transmission and risks of severe outcomes; the rise of each variant was captured by additionally fitting to the proportion of S-gene target failures (a measure of variant-type) from TaqPath PCR testing [8, 9]. Early models used in the initial assessment of vaccine dose intervals only considered wildtype and Alpha variants, although the work presented here also includes the Delta variant.
The start of the vaccination campaign in December 2020 necessitated a further partitioning of the population by vaccination status, allowing us to capture both the reduced risk of infection and the reduced risk of severe outcomes. However, it became clear during 2021 that the vaccines (and to a less extent infection) did not confer long-lasting immunity and therefore waning levels of protection both in terms of vaccine-induced and infection-induced immunity were added (generating additional elements within the model). This is shown schematically in Fig.S1, focusing on vaccination and waning immunity; for simplicity the structure within the infection process is not fully represented (which includes variant structure), and the full model is also partitioned into age group and seven different spatial regions for the dynamics in each of the NHS regions.
We now provide more details of the individual components that combine to generate the full model.
Showing the progress of two-dose vaccination, waning protection (light blue) and boosters (dotted purple). The infection compartment is multi-dimensional, capturing latent and infectious classes as well as variant type. Severe outcomes (hospital or ICU admission and death) are related to the level of infection in each age-group and their degree of vaccine (or infection-induced) protection.
Infection modelling
As is common to most epidemiological modelling we stratify the population into multiple disjoint compartments and capture the flow of the population between compartments in terms of ordinary differential equations. At the heart of the model is a modified SEIR equation, where individuals may be susceptible (S), exposed (E), infectious with symptoms (I), infectious and either asymptomatic or with very mild symptoms (A) or recovered (R). Both symptomatic and asymptomatic individuals are able to transmit infection, but asymptomatic infections do so at a reduced rate given by τ. Hence, the force of infection is proportional to I + τA. To some extent, the separation into symptomatic (I) and asymptomatic (A) states within the model is somewhat artificial as there are a wide spectrum of symptom severities that can be experienced, with the classification of symptoms changing over time. Our classification reflects early case detection, when only relatively severe symptoms were recognised.
To obtain a better match to the time from infection to becoming infectious, we model the exposed class as a three-stage process, such that in a stochastic formulation the distribution of the latent period would be an Erlang distribution.
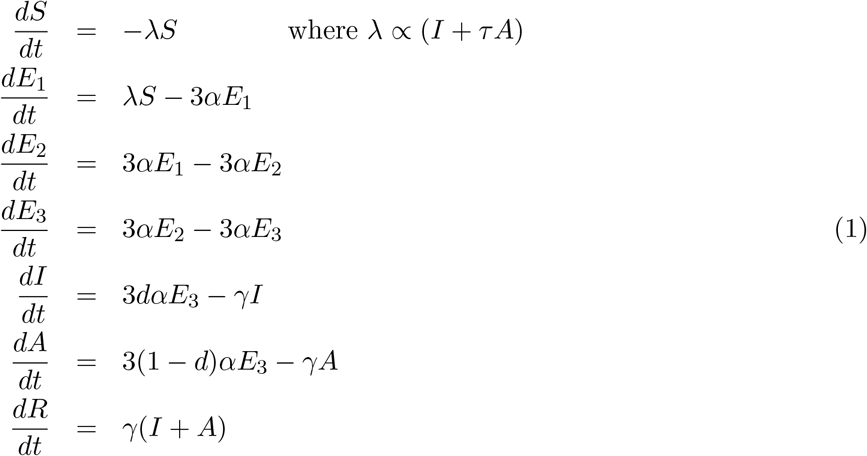where α−1, and γ−1 are the mean latent and infectious periods, while d is the proportion of infections that develop symptoms.
Age Structure and Transmission Structure
We expanded the simple model structure (equation 1) to twenty-one 5-year age-groups (0-4, 5-9,…, 95-99, 100+). Age has three major impacts on the epidemiological dynamics, with each element parameterised from the available data:
Older individuals have a higher susceptibility to SARS-CoV-2 infection (captured by the parameter σ).
Older individuals have a higher risk of developing symptoms, and therefore have a greater rate of transmission per contact.
Older individuals have a higher risk of more severe consequences of infection including hospital admission and death.
The age-groups interact through four who-acquired-infection-from-whom transmission matrices, which capture the epidemiological relevant mixing in four settings: household (βH), school (βS), workplace (βW) and other (βO). We took these matrices from Prem et al. [10] to allow easy translation to other geographic settings, although other sources could be used.
One of the main modifiers of mixing and therefore transmission is the level of precautionary behaviour, ϕ [11]. This scaling parameter changes the who-acquired-infection-from-whom transmission matrices in each transmission setting, such that when ϕ = 1 mixing in workplaces and other settings take their lowest value, whereas when ϕ = 0 the mixing returns to pre-pandemic levels [1]. Mixing within the school setting followed the prescribed opening and closing of schools. The age-structured model therefore becomes:
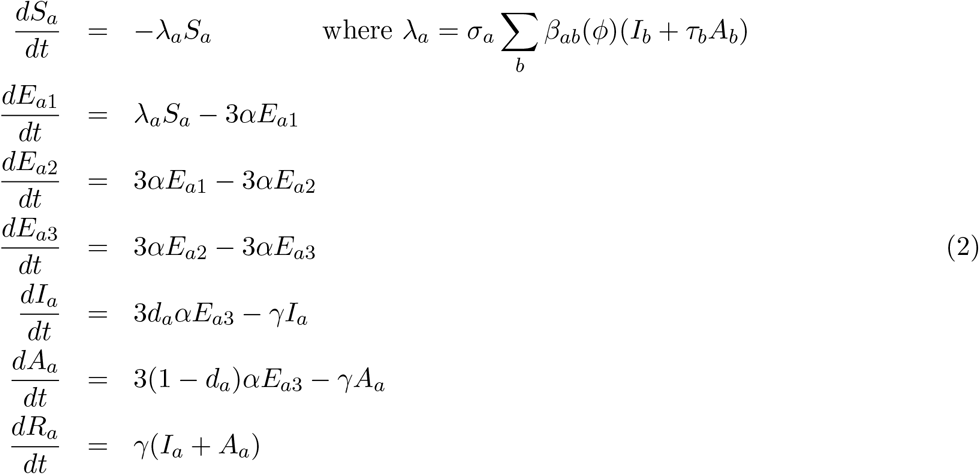
For simplicity of notation, we write the sum of the four age-structured mixing matrices as β(ϕ), explicitly recognising its dependence on the time-varying level of precautionary behaviour (either imposed of voluntary) within the population.
To ensure that we can replicate the long-term dynamics of infection we allow the population to age. The ageing process occurs annually (corresponding to the new school year in September) in which approximately one fifth of each age-group moves to the next oldest age cohort — small changes to the proportion moving between age-groups are made to keep the total population size within each age-group constant.
Capturing Quarantining and Isolation
One of the key characteristics of the COVID-19 pandemic in the UK has been the use of self-isolation and household quarantining to reduce transmission. We approximate this process by distinguishing between first infections (caused by infection related to any non-household mixing) and subsequent household infections (caused by infection due to household mixing). The first symptomatic case within a household (which might not be the first infection) has a probability (H) of leading to household quarantining; this curtails the non-household mixing of the individual and all subsequent infections generated by this individual.
In our notation, we let superscripts denote the first infection in a household (F), a subsequent infection from a symptomatic household member (SI) and a subsequent infection from an asymptomatic household member (SA); the first detected case in a household who leads to household quarantining (QF) and all their subsequent household infections (QS). For a simple SEIR model (ignoring multiple E categories and age-structure) our extension would give:
where λF = (βS + βW + βO)(IF +ISI + ISA + τAF + τASI + τASA)
This formation has been shown to be able to reduce the reproductive ratio, R, below one even when there is strong within household transmission, as infection from quarantined individuals cannot escape the household [12].
Spatial Modelling
Within England the model operates at the scale of seven NHS regions (East of England, London, Midlands, North East, North West, South East and South West). For simplicity and speed of simulation we assume that each of these regions acts independently and in isolation - we do not model the movement of people or infection across borders. In addition, the majority of parameters are regionally specific, reflecting different demographics, deprivation and social structures within each region. However, we include a hyper-prior on the shared parameters such that the behaviour of each region helps inform the value in others.
Variant Modelling
The model also captures the three main SARS-CoV-2 variants that have been responsible for most infections in England during 2020 and 2021: the wildtype virus (encapsulating all pre-Alpha variants), the Alpha variant and the Delta variant. Each of these requires a replication of the infectious states for each variant type modelled. We assume that infection with each variant confers immunity to all variants, such that there is indirect competition for susceptible individuals. This competition is driven by the transmission advantage of each variant which is estimated by matching to the proportion of positive community PCR tests (Pillar 2 test) that are positive for the S-gene. The TaqPath system that is used for the majority of PCR tests in England is unable to detect the S-gene in Alpha variants, due to mutations in the S-gene. The switch from S-gene positive to S-gene negative and back to S-gene positive corresponds with the dominance of wildtype, Alpha and Delta variants. We infer the transmissibility of Alpha and Delta variants to be 52% (CI 35-71%) and 156% (CI 117-210%) greater than wildtype, respectively.
Vaccination Modelling
We capture vaccination using a leaky approach, although non-leaky (all-or-nothing) models produce extremely similar results over the time-scales considered. The model replicates the action of:
first and second doses of vaccine, at rates v1 and v2 respectively, that move susceptible individuals through to vaccinated states (V S1 and V S2) but have no impact on infected or recovered individuals - for model simplicity v1 and v2 correspond to the when the impact of the dose takes effect which is around 10 days post vaccination;
waning vaccine efficacy at rates ω1 and ω2, giving a two-step process from fully vaccinated to waned efficacy (we also allow waning from state S1, although for those that receive two doses within 3 and 12 weeks this is uncommon);
waning immunity from past infection at rates Ω1 and Ω2 which are assumed to be slower than the waning of vaccine efficacy.
The model also needs to capture the total number of individuals who have been given a first or second dose of vaccine (V1 or V2 out of a total population size of N) to ensure that only individuals that have not been vaccinated are offered a first dose, and only individuals that have been vaccinated once are offered a second dose.
Ignoring infection and concentrating on vaccination and waning immunity, the underlying equations become:
For those in the classes where the vaccines generate protection (V S1, V S2, WS1 and WS2), the degree of protection is determined by the protection offered by each vaccine type (Table S1), weighted by the ratio of AstraZeneca (ChAdOx1) vaccine to mRNA vaccines (either Pfizer BNT162b2 or the Moderna COVID-19 vaccine) that had been given to that age group. If a vaccinated individual becomes infected, their probability of being admitted to hospital or dying - which normally only depends on age - is again modified by the appropriate vaccine efficacy according to the ratio of the two vaccine types deployed within that age-group. This leads to a noticeable decline in vaccine efficacy against infection and disease (Fig.S2, left hand panel) but a much slower drop in the level of protection against hospital admission and death (Fig.S2, centre and right hand panels).
Assumed percentage protection from the two vaccine types against the Alpha and Delta variants after one dose (D1), after two doses (D2, shown for the dose interval gaps of 12-weeks/3-weeks), and after waning (W). These values correspond to relatively slow waning of vaccine protection (ω1 = 48−1 per day, ω2 = 320−1 per day,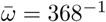 
per day) [13,14].
Data are taken from UKHSA estimates in December 2021 [13]; data is shown for the Pfizer vaccine (blue diamonds), AstraZeneca vaccine (red circles) and the weighted average (grey), the model obeys the simple compartmental rules described above. The vertical lines represent the 95% confidence intervals, capturing uncertainty in the data; while the horizontal lines correspond to the period over which the data is amalgamated.
Impact of Shorter Dose-Interval on Vaccine Efficacy
When focusing on the impact of a shorter dose-interval, we considered a scenario where vaccine efficacy remained unaffected and a scenario in which efficacy was reduced. For the scenario where a shorter dose-interval resulted in a reduced efficacy, the reduction in efficacy was guided by the analyses of Khoury [15] (Fig.S3 left-hand panel), which linked the level of neutralising antibodies to the degree of vaccine protection, and the experimental work of the Com-COV group [16], which highlighted the lower level of neutralising antibodies with a shorter interval between vaccine doses. We took efficacy estimates after the second dose using 12-week intervals from UKHSA studies [13] and translated via a three-step process into the reduced efficacy at 3 or 4 weeks (Fig.S3 central panel). The resultant values are shown in the right-hand panel of Fig.S3, and are given in Table 1.
Left-hand panel shows the data (dots) and fitted curve (red line) from [15] that translates neutralisation level (relative to that for convalescent) to the degree of protection against symptomatic disease. Central panel shows the steps needed to scale efficacy for a 12-week dose interval to that for a short 3- or 4-week dose interval: (A-B) 12-week efficacy is translated to a relative neutralisation level via the red curve [15]; (C) neutralisation level is reduced according to the values obtained by the Com-COV study [16]; (D-E) the reduced neutralisation level is translated to a reduced efficacy for the shorter dose interval. Right-hand panel shows the consequences of this process for the AstraZeneca (AC) and Pfizer (PF) vaccines against the Alpha and Delta variants.
Parameter Inference
Key to the accuracy of any model are the parameters that underpin the dynamics. With a model of this complexity, a large number of parameters are required. Some, such as vaccine efficacy, are assumed values based on the current literature; while others are inferred from the epidemic dynamics.
Of the inferred parameters there are three basic classes; those, such as scalings of the case-hospitalisation ratios, that are different between regions and variants; others such as age-dependent susceptiblity are universal (the same for all regions and variants); while the level of precautionary behaviour over time changes on a weekly time-scale. Bayesian inference, using an MCMC process, is applied to each of the seven NHS regions in England to determine posterior distributions for each of the regional parameters (further details are given in [7]). The distribution of parameters leads to uncertainty in model projections, which is represented by the 95% prediction interval in all graphs (this interval contains 95% of all predictions). We note that when we compare two scenarios (for example vaccination with a 3-week interval, with vaccination using a 12-week interval) we compared simulations with the same parameters chosen from the posterior distributions - and then calculated means and 95% prediction intervals based on these results.
As the epidemic has progressed, new posterior distributions based on the latest data are initialised from previous MCMC chains – ensuring a rapid fit to historical data. In general this refitting process has been performed weekly (or twice weekly) throughout the pandemic. For the time period of relevance in this paper (December 2020 - September 2021), we matched to six observations: hospital admissions, hospital occupancy, ICU occupancy, deaths, proportion of pillar 2 (community) test that are positive, and the proportion of pillar 2 tests that are S-gene positive (as a signal of the ratio of wild-type to Alpha variant, then a signal of the ratio of Delta to Alpha variant). We note that in [7], which was written in the early stages of the pandemic, we did not fit to S-gene data as we had been dealing with a single variant. Although not part of the underlying transmission dynamics, these six quantities for each spatial region can be generated from the number, age and type of infection within the model. We compared observations and model results by considering the likelihood of generating the observations assuming them to be Poisson distributed (for numbers) or binomially distributed (for proportions) with a mean given by the results of the deterministic model.
Comparison between Model and Data for Age-structured Severe Disease
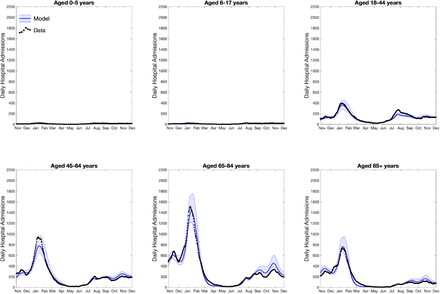
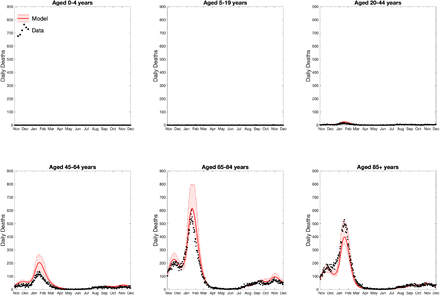
It has been clear throughout the pandemic that age-structure plays a major role in both the acquisition of infection and the severity of disease - with the risk of hospital admission and death increasing rapidly with age. In the main text we compare model results with data for the entire population, focusing on the total daily number of hospital admissions (associated with a positive COVID-19 test) and the total number of daily deaths (within 28 days of a positive test). Here we extend this comparison, plotting data and model results on the same figure for six different age ranges (Fig.S4 and Fig.S5). We note that the age-groups for which hospital admissions are reported do not necessarily correspond with the 5-year age bins used within the model simulations. We assume homogeneity within an age-group in the model (i.e. all individual aged 0 to 4 have the same mean risk of infection and hospital admission); this means that when computing the expected number of daily admissions for those aged 6-17, for example, we sum 80% of the second age-group in the model (age 5-9), 100% of the third age-group (age 10-14) and 60% of the forth age-group (age 15-19). For deaths, from the empirical data we know the age of each person in years and so are able to make a comparison to simulated outputs using an amalgamation of 5-year age groups.
It should be noted, as described above, that the inference processes only use aggregate (non-age-structured) data to determine the match between model and the unfolding epidemic. The exception is the risk of hospital admission and death following infection, which for each variant of concern are matched to the total reported for each age group. In general we find that during the second wave (December 2020 - March 2021) the model tends to slightly under-estimate hospital admissions and over-estimate deaths in the 45-64 age group. However, it captures the bulk properties of the waves, especially the dominance of severe disease in older age-groups.
We depict the data as solid black dots and results from the model simulations in blue. The solid lines corresponds to mean values and the shaded area shows the 95% prediction interval (i.e. it contains 95% of all predictions at each point in time).
We depict the data as solid black dots and results from the model simulations in red. The solid lines corresponds to mean values and the shaded area shows the 95% prediction interval (i.e. it contains 95% of all predictions at each point in time).
Acknowledgements
MJK was supported through the JUNIPER modelling consortium [grant number MR/V038613/1]; MJK and SM were supported by the National Institute for Health Research (NIHR) [Policy Research Programme, Mathematical and Economic Modelling for Vaccination and Immunisation Evaluation, and Emergency Response; NIHR200411]; MJK and EMH were supported by the Medical Research Council through the COVID-19 Rapid Response Rolling Call [grant number MR/V009761/1] MJK is affiliated to the National Institute for Health Research Health Protection Research Unit (NIHR HPRU) in Gastrointestinal Infections at University of Liverpool in partnership with UK Health Security Agency (UKHSA), in collaboration with University of Warwick. MJK is also affiliated to the National Institute for Health Research Health Protection Research Unit (NIHR HPRU) in Genomics and Enabling Data at University of Warwick in partnership with UK Health Security Agency (UKHSA). The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR, the Department of Health and Social Care or UK Health Security Agency.
References
References
