Antibody selection strategies and their impact in the analysis of malaria multi-sera data

André Fonseca, Mikolaj Spytek, Przemyslaw Biecek, Clara Cordeiro, Nuno Sepúlveda
doi: https://doi.org/10.1101/2022.10.06.22280719

Abstract

Background Nowadays, the chance of discovering the best antibody candidates for explaining naturally acquired protection to malaria and detecting exposure to malaria parasites has notably increased due to publicly available multi-sera data. The analysis of these data is typically divided into a feature selection phase followed by a predictive one where several models are constructed for the outcome of interest. A key question in the analysis is to determine which and how each feature should be included in the predictive stage.

Results To answer this question, we developed three approaches for classifying malaria protected and susceptible groups: (i) a basic and simple approach based on selecting antibodies via the nonparametric Mann-Whitney test; (ii) a dichotomization approach where each antibody was selected according to the optimal cut-off via maximization of the χ2 statistic for two-way tables; (iii) a hybrid parametric/non-parametric approach that integrates Box-Cox transformation followed by a t-test, together with the use of finite mixture models and the Mann-Whitney test as a last resort. We illustrated the application of these three approaches with published serological data for predicting clinical malaria in 121 Kenyan children. The predictive analysis was based on a Super-Learner where predictions from multiple classifiers were pooled together. Our results led to almost similar areas under the Receiver Operating Characteristic curves of 0.72 (95% CI = [0.61, 0.82]), 0.80 (95% CI = [0.71, 0.90]), 0.79 (95% CI = [0.7, 0.88]) for the simple, dichotomization and hybrid approaches, respectively.

Conclusions The three feature selection strategies provided a better predictive performance of the outcome when compared to the previous results solely relying on Random Forests alone (AUC=0.68). Given the similar predictive performance, we recommended the three strategies should be used in conjunction in the same data set and selected according to their complexity.

Background

Multi-sera data, where multiple antibody targets are measured in blood samples from the same individual, are becoming widely available in malaria research due to substantial developments at the level of serological assays1–4. This public availability has boosted basic research on the discovery of key antibodies associated with protection to malaria5–10. Moreover, it also motivated the development of serological-based algorithms that could predict not only past exposure to malaria parasites11,12 but also time since the last infection13. It has been suggested that these algorithms could help to design better malaria control strategies such as the serological testing and treatment (seroTAT) approach based on 8 antibodies for detecting Plasmodium vivax cases that should be targeted to receive an anti-hypnozoite therapy12.

In these multi-sera studies, the total number of antibody targets varied from dozens8,10,13 to thousands6,7,14. This number generates a huge computational cost for algorithms that search for the best model for the data. To overcome this problem, a brute-force approach (where every possible antibody combination is tried out) is computationally feasible for no more than 5 antibody targets8. However, it is not recommended above that number10,12.

This computational drawback motivated the use of data analysis strategies that are generically divided into an antibody or feature selection stage, followed by a predictive one, in which several statistical or machine learning models are estimated from the data7,9,10,13,15. In this scenario, the initial antibody selection stage determines the predictive performance of the models to be constructed in the following stage.

Antibody selection can be formulated as the procedure to determine which antibodies are associated with the outcome of interest16–18. However, this question hides another one in which one should decide whether data transformation, including dichotomization, should be used. Data transformation is particularly relevant in multiplex serological assays because distinct data distributions might emerge due to differences in the calibration curves across antibodies, as demonstrated in assay-optimization studies16–18. Until now, antibody selection has been carried out using only raw or untransformed5,6 data or seroprevalence-like data but10,12 without any combination of both. Additionally, the transformation of each antibody data is typically not considered. Therefore, current antibody selection procedures for multi-sera data lacks the flexibility to accommodate different data patterns. The current study tackles this issue and shows that it can potentially increase the chance of obtaining improved outcome predictions.

This paper presents a general parametric strategy for antibody selection in which a combination of transformed and dichotomized antibody data can be selected for the predictive phase. This strategy add flexibility to feature selection by combining the Box-Cox data transformation with well-known parametric statistical tests. A second, and simpler, strategy is also presented in which data of each antibody is initially dichotomized using an optimal cut-off point in the antibody distribution based on the maximization of the chi-square test statistic. Lastly, the predictive performance of these strategies was compared with the performance of the basic approach, where the statistical significance for the nonparametric Mann-Whitney-Wilcoxon test was obtained for each antibody, comparing the protected and susceptible groups. To illustrate these three strategies, we analyzed a published dataset on Immunoglobulin G (IgG) antibody responses to 36 Plasmodium falciparum (Pf) antigens in Kenyan children to understand protection to clinical malaria8 and whose data analysis was previously done with Random Forest15.

Methods

Data under analysis

We re-analyzed published data of 121 Kenyan children (age range: 1-10 years of age) described in detail elsewhere8. All children had a documented parasitaemia (parasite-positive) at the time of sampling and were monitored for clinical episodes of malaria over a follow-up period of 6 months. As in the original publication, children were considered susceptible (Sus, ns=40) or protected (Prt, np=81, 33%) if they had or did not have any clinical episode during the follow-up period. The serological data referred to individual IgG antibody responses to 36 Plasmodium falciparum antigens. These antibody responses were measured by multiple enzyme-linked immunosorbent assays (ELISA). Detailed information about recruitment, study design and experimental protocols, among other aspects of this early research, can be found in the original publication8.

Preliminary antibody feature selection using Random Forest

The Random Forest works by constructing multiple decision trees trained on different parts of the same training set by a resampling process called bootstrap aggregation or bagging19. Random Forests were implemented by repeatedly fitting the model to 1000 resampled subsets of the data (100 repeats of 10-fold cross-validation). For each repetition, the dataset was divided into 10-cross-folds, of which 9-folds were used to perform an inner 10-fold cross-validation20. The number of trees to grow and the number of predictors randomly sampled as candidates in each split was set to default21 (number of trees = 500; number of predictors randomly selected = 2, 19 and 36), and the optimization criteria was maximization of the area under the of Receiver Operating Characteristic (ROC) curve, known as AUC22. Feature importance was given by the mean decrease in accuracy23. Briefly, for each tree, the prediction accuracy on the out-of-bag portion of the data is recorded. Then, after permuting each predictor variable, the prediction accuracy on the out-of-bag portion of the data is once again recorded. The difference between the two accuracies are then averaged over all trees, and normalized by the standard error23.

Antibody selection based on the simple approach

The first antibody selection strategy was to select the antibodies by their statistical significance according to the non-parametric Mann-Whitney-Wilcoxon test comparing the protected and susceptible groups in each antibody data24.

Antibody selection based on the data dichotomization approach

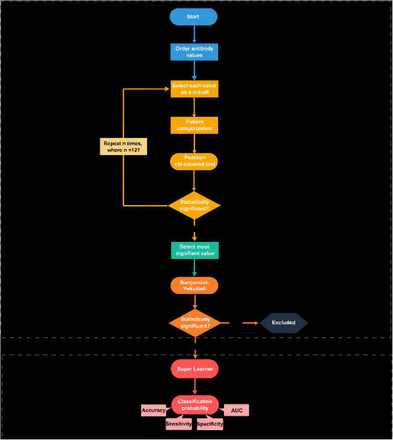
The second antibody selection strategy was based on a procedure in which the optimal cut-off to differentiate one study group from another was estimated by maximizing the chi-squared (χ2) statistic for testing independence in two-way contingency tables, as done elsewhere25,26 (Figure 1). In more detail, the values of each antibody were sorted by increasing order and then used to divide individuals into two latent serological groups (i.e., seronegative/seropositive individuals or high/low responders). For each value of a given antibody, the resulting data was summarized into a two-way contingency table comprising the qualitative variables serological status (below/above the cut-off) and malaria protection status (protected/non-protected). The χ2 test statistic was then calculated for this contingency table. After repeating this procedure for all antibody values, the optimal cut-off was selected as the value that maximized that test statistic, meaning the one that provided the best discriminatory ability between both groups of patients. After selecting the optimal cut-off, we calculated the respective p-value associated of the χ2 test. The dichotomized data was then used for the predictive phase. Finally, this procedure was repeated for each of the 36 antibodies included in the dataset.

Figure

Antibody selection based on the hybrid parametric/non-parametric approach

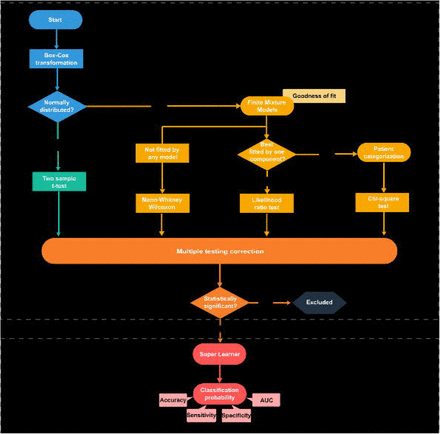
We adopted an alternative antibody selection approach using different parametric models or statistical tests (Figure 2). In the first step, we determined the optimal Box-Cox transformation for each antibody. This transformation was sought to obtain normal distributions with homogeneous variances in both groups. We searched the best parameter of this transformation (hereafter denoted as λ) within the interval (-4;4) by maximizing evidence for a Normal distribution using the Shapiro-Wilk (SW) test where the null hypothesis states that the data come from a normal distribution (with unknown parameters)27. A significance level of 5% was specified to assess whether the data of each antibody could follow a normal distribution.

Figure

For the antibodies where there was no evidence against the normal distribution, we calculated the p-value for the t-test aiming at comparing the mean values of the susceptible and protected groups. The remaining antibodies, where there was evidence against the normal distribution, were then evaluated via finite mixture models given that it is recurrent to find latent populations in serological data28. Using transformed data, we estimated two-component mixture models based on Normal, Generalized t, Skew-Normal and Skew-t distributions by maximizing the likelihood function via the Expectation-Maximization algorithm29. We also estimated the Generalized t, Skew-Normal and Skew-t distributions to assess the evidence that the data could come from a single non-Normal serological population beyond the ones identified by the Box-Cox transformation. We compared all these models using the Akaike’s Information Criterion (AIC) and performed the Pearson’s goodness-of-fit test by dividing the respective data into deciles (i.e., 10%-quantiles). Minimization of the AIC, together with a good fit to the data, at the significance level of 5%, was the criterion for selecting the best model. For antibodies whose data provided evidence of two latent serological populations, we divided the individuals into two latent serological groups using the optimal cut-off by maximization of the χ2 statistic (as described in the previous section). For the antibodies in which there was evidence of a single latent serological population antibody, we constructed two linear regression models using the antibody values as the response variable. The first model comprised only the intercept (i.e., not including any covariate), while the second model comprised the malaria protection status as the single covariate. We then computed the p-value of the Wilks’s likelihood ratio test to compare the two models at the significance level of 5%. The rejection of the null hypothesis suggested statistically significant differences between the two models being compared. Finally, antibodies that could not be fitted by any of the above parametric models were analyzed through a non-parametric Mann-Wilcoxon test to compare the median values of the protected and susceptible groups.

Correction for multiple testing

In each antibody selection strategy, all the p-values obtained were adjusted to ensure a global false discovery rate (FDR) of 5%. This p-value adjustment was made via the Benjamini-Yekutieli procedure under a general dependence assumption between tests30. All antibodies whose adjusted p-values < 0.05 were carried to the predictive analysis.

Predictive Stage

When analyzing data resulting from each antibody selection strategy, we adopted a Super-Learner (SL) approach to predict the malaria protection status of each individual31,32. In general, this approach aims to estimate different (mostly data-driven) classifiers whose individual predictions for each individual are combined into a pooled estimate via a weighted average calculated by cross-validation. To construct this pooled estimator, we used the following 5 classifiers for each set of antibodies selected: logistic regression model (LRM) with main effects only, Random Forest (RF), linear discriminant analysis (LDA), quadratic discriminant analysis (QDA), and extreme gradient boosting (XGB). For the antibodies selected by optimal dichotomization antibody selection strategy, we did not include linear and quadratic discriminant analyses in the SL algorithm because these classifiers are more appropriate for data containing quantitative predictors only.

To assess the quality of the final predictions, we estimated the ROC curve and its area (AUC)22,33. In addition, we calculated the confusion matrices where the rows and columns represented the predicted and the observed status of the individuals, respectively34. These confusion matrices were calculated using the point in the ROC curve that minimizes the distance to the point (0,1) related to the perfect classification of the individuals, here called ROC01 criterion35. From the standpoint of constructing a fair classifier36,37, we also determined the predictive performance by the point in the ROC curve in which sensitivity (protected) and specificity (susceptible) were equal approximately35. This criterion is hereafter denoted as SpEqualSe criterion35.

Statistical Software

All statistical analyses were implemented in the R38 version 4.3.0 using the following packages: “AID” to perform Box-cox transformation and to compute the respective Normality tests39; “caret” to construct the confusion matrices23; “doParallel” for parallel processing and faster run times40; “dplyr” to better manipulate the data41; “ggplot2” to plot the data42; “ggrepel to avoid overlaid text on plots43; “lmtest” to perform the likelihood ratio test44; “MASS” for general analysis45; “mixsnsm” to estimate mixture models based on Skew-Normal and Skew-t distributions46; OptimalCutpoints to obtain the point in the ROC curve that minimizes of the distance to the point (0,1)35; “pROC” to estimate ROC curves47; “sn” to perform linear regression models based on Skew-Normal or Skew-t distributions for the residuals48; “SuperLeaner” to perform all the predictive analysis31; “tydir” to facilitate data manipulation49.

RESULTS

Preliminary analysis based on the Random Forest approach

Initially, a Random Forest model was implemented on all 36 antibodies replicating the approach conducted by Valleta and Recker15. According to our findings, we were able to reproduce the previously reported AUC of 0.6815 (Figure 3A). Looking at the feature importance values, we concluded that all except one of the 36 antibodies were required to achieve this predictive performance (Figure 3B). Nevertheless, a more thorough analysis of the feature’s importance values reveals that several features had very low importance values (below 20% importance) (Figure 3B). This led us to hypothesize that removing these features could improve the model’s performance. Therefore, three distinct filter strategies for feature selection were used.

Figure

Analysis based on the simple antibody selection approach

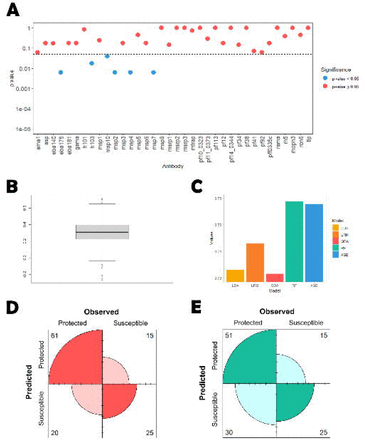
We first tested whether levels of each antibody were significantly different between susceptible and protected individuals using the Mann-Whitney-Wilcoxon test. According to this nonparametric test, twenty-one out of the 36 antibodies were found statistically significant before adjusting for multiple testing. This number dropped to six after controlling for an FDR of 5%: msp2, msp4, msp10, eba175, msp7, and h103. This substantial reduction in the number of significant antibodies is likely to be explained by the positive correlation among different antibodies (average Spearman’s correlation coefficient = 0.312; Figure 4A). As expected, the levels of these selected antibodies were elevated in the protected individuals (Figure 4B).

We then constructed a Super-Learner classifier based on the data of these 6 antibodies. The average estimates for the AUC were 0.713, 0.703, 0.702, 0.729 and 0.728 using LRM, LDA, QDA, RF and XGB, respectively (Figure 4C). The average weights of these classifiers were 0.089, 0.506, 0.035, <0.001, and 0.370 in the final predictions, respectively. These weights implied an AUC of 0.719 (95% CI=(0.615, 0.824)) for the SL predictions.

Figure

Moreover, the SL predictions had a sensitivity of 0.753 and a specificity of 0.625 according to the ROC01 criterion (Figure 4D). A higher number of protected individuals in the dataset could explain the fact that sensitivity was estimated at a higher value than specificity. To assess the final classifier without this potential selection bias, we determined the point at which the ROC sensitivity and specificity were similar and used it to obtain a fair classification (SpEqualSe criterion). The balanced sensitivity and specificity estimates were 0.630 and 0.625, respectively (Figure 4E).

Analysis based the data dichotomizations approach

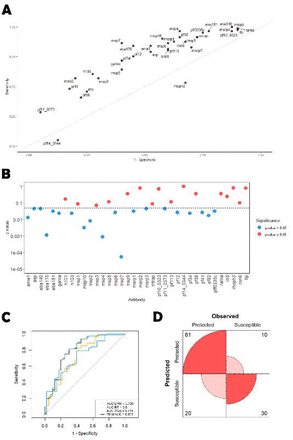
In this analysis, we determined the optimal classification cut-off for each antibody according to the χ2 statistics. The sensitivity using these optimal cut-offs varied from 0.049 (pf14_0344) to 1 (eba140, msrp3), while the specificity varied from 0.100 (msp9) to 0.95 (pf11_0373). The top 3 antibodies whose optimal cut-offs provided the sensitivity and specificity estimates closest to perfect classification (i.e., specificity=sensitivity=1) were msp7 (Se=0.852, Sp=0.600), eba175 (Se=0.827, Sp=0.550), and msp2 (Se= 0.556, Sp=0.800; Figure 5A).

Figure

There were 28 out of 36 antibodies whose proportions above the optimal cut-off were significantly different between protected and susceptible individuals at the 5% significance level (Table 1). However, after controlling for an FDR of 5%, the number of statistically significant antibodies dropped to 20 (Figure 5B). The dichotomized data of these antibodies, according to the optimal cut-off, was used for predictive analysis.

View this table:
Table 1 Patient Seroprevalence.

The statistically significant results of the χ2 test for the 28 antibodies. The antibody levels that maximized the separation between the susceptible and protected group of individuals (Cut-off) and the proportion of seropositive individuals for all (Total), Protected (Prt) and susceptible (Sus) children, respectively

The AUC of the SL-based predictions was estimated at 0.801 (95% CI=(0.709, 0.892)) (Figure 5C), which showed an improvement from the previous analysis using a non-parametric antibody selection. The average AUC (and weights) estimates for each classifier were: LRM -0.729 (<0.001), RF -0.800 (0.973), and XGB – 0.714 (0.026). This result showed that, notwithstanding the reasonable AUC estimates for LRM and XGB, the final predictions were basically derived from the RF classifier. Note that LDA and QDA were not included in the SL algorithm, as they are more suitable for analyzing quantitative multivariate data.

According to the ROC01, the final sensitivity and specificity were estimated at 0.753 and 0.750, respectively. These estimates were identical for the SpEqualSe criterion. In conclusion, this analysis produced a combined classifier that exhibited an improved and better-balanced predictive performance than the previous one. However, this classifier had the disadvantage of including a higher number of antibodies comparing compared to the previous one (20 antibodies versus 6 antibodies).

Analysis based on the hybrid parametric/non-parametric approach

We first estimated the Box-Cox optimal data transformation and applied it to the antibody data. Then, we compared the protected and susceptible groups using the parametric t-tests for two independent samples. Our findings suggested that there were 6 antibodies whose data in each study group could be analyzed by these tests after the Box-Cox transformation: asp, pf11_0373, pf14_0344, pf34, rh5, and ron6 (Figure 6A); note that, at this stage, we did not adjust the p-values of the respective goodness-of-fit tests due to multiple testing, because such adjustment would increase the evidence for the null hypothesis of these tests. In these antibodies, the estimates for the parameter l of the Box-Cox transformation varied from -3.8 (ron6) to -0.78 (pf34). The estimates suggest that the logarithmic transformation would not be the best to generate a normal distribution. The best evidence for a Normal distribution was found for pf34 with a p-value of 0.75 using the Shapiro-Wilk test (Figure 6A).

The remaining 30 antibody data were then analyzed by fitting finite mixture models based on Normal, Generalized T, Skew-normal, and Skew-T distributions; note that Normal and t distributions come as special cases of the latter probability distributions. For the statistical convenience of having these antibodies defined in terms of positive and negative values, we log-transformed the respective antibody data.

Figure

We found evidence that data from 7 antibodies could be described well by either Skew-Normal (msp3 and h103) or Skew-t (gama, h101, msrp2, msrp3, and pf10_0323) distributions (Table 2). In this case, the comparison between study groups was made via regression models using these distributions for the errors. Except for the antibodies against pf92 and ama1, data of the remaining antibodies were best described by a mixture of two Normal distributions (4 antibodies), two Skew-Normal distributions (16 antibodies) or two Skew-t distributions (1 antibody; see Table 2). The best fit of these mixture models was obtained for the antibody against pf113 using a two-component Normal mixture model (p=0.73, Pearson’s goodness-of-fit test; Table 2). For these antibodies, we assumed the existence of a seronegative and a seropositive population. We dichotomized the respective data using the optimal cut-off by maximization of the χ2 test statistic. Data of the antibodies against pf92 and ama1 could not be fitted by either Normal distribution after Box-Cox transformation or using the above mixture models. Therefore, we used the Mann-Whitney-Wilcoxon test as the last resort statistical test to compare the protected and susceptible groups. Thus, comparing the protected and susceptible groups using the different tests led to 25 significant antibodies before applying a multiple testing correction This number decreased to 16 after ensuring an FDR of 5%. These antibodies were found to be significant by the Wilks’ likelihood ratio test (msp3, msrp3 and h103), the c2 test (eba175, eba181, msp2, msp4, msp6, msp7, msp10, msrp1, pf12, pf41, pff0335c) and the Mann-Whitney-Wilcoxon test (pf92, ama1) (Figure 6B). In the predictive analysis, data of each antibody were included in the SL approach according to the suggested scale by the antibody selection procedure: log-transformed data for antibodies coming from the Wilks’ likelihood ratio test, dichotomized seropositive/seronegative data for antibodies coming from the c2 test, and the original scale for the pf92 and ama1-related antibodies coming from the Mann-Whitney-Wilcoxon test. Before obtaining the combined predictions, we checked each individual classifier’s performance. The average AUC were 0.756, 0.807, 0.768, 0.656 and 0.643 using LRM, RF, LDA, QDA, and XGB, respectively. Therefore, the best individual classifier was the RF. The average weights of these classifiers were 0.021, 0.912, 0.0132, 0.053, and 0 in the final predictions, respectively, resulting in an AUC of 0.78 CI=(0.7, 0.879)) According to the ROC01 criterion, the sensitivity and specificity were estimated at 0.703 and 0.750, respectively (Figure 6C). Moreover, based on the ROC curve, the best balance between these quantities was obtained for a sensitivity and a specificity of 0.716 and 0.725, respectively (Figure 6D).

View this table:
Table 2 Analysis based on Finite Mixture Model.

Results from the analysis of 28 antibodies based on finite mixture models where AIC and GOF denote the Akaike’s information criterion and Pearson’s goodness-of-fit test, respectively.

Discussion

Multi-sera data, where thousands of antibody targets are simultaneously measured, can increase the chance of discovering the best antibody candidates for explaining natural protection to malaria and detecting exposure to malaria parasites50–52. Nonetheless, this type of data brings novel challenges53,54. One of the main drawbacks when dealing with this type of data is the difficulty of identifying the relevant features for the task at hand. Among the thousands of features screened, most will be irrelevant or redundant and will negatively impact the predictive ability of a predictive model55. Not only that, trying to fit a predictive model to these many features increases the computational complexity and cost, reduces the model generalization ability, and affects the explainability of the model54. To overcome these limitations, feature selection strategies have been proposed, where the aim is to identify and remove all the irrelevant features so that the learning algorithm focuses only on those features of the training data useful for prediction53. This leads not only to a simpler interpretability, as when a small number of features is selected their biological relationship with the target disease is more easily identified, but also into a lower computational cost and increased accuracy stemmed from reducing the chance of overfitting54,56. Therefore, feature selection before the implementation of a predictive model is strongly advocated57. Amongst the different feature selection approaches, here we opted for the use of filter methods53,56,57. These rely on statistical measures (e.g p-value, correlation coefficient), and their application precedes the predictive phase, thus being independent of any predictive model56,57. For this reason, they are usually very fast to implement. Here we will discuss the advantages and drawbacks of the distinct filter methods employed in each proposed methodology. The simple approach relying on the Mann-Whitney Wilcoxon test for feature selection is the most scalable approach for larger datasets among the ones here proposed. It is the most straightforward and fastest approach to implement, making it an appealing tool for those looking for a low complexity model when conducting a classification task. Moreover, given its ranking intrinsic nature, this strategy represents the best option to achieve reproducible results24. Nevertheless, its low statistical and computational complexity comes at a cost since this feature selection approach might led to a lower predictive performance when compared to the other strategies, as demonstrated in this study. Concerning the data dichotomization methodology performance, we can see that, unsurprisingly, it was the one with better predictive performance and therefore, this methodology can be seen as the optimistic case scenario. The use of the χ2 test for feature selection is very straightforward to implement and has a low computational complexity making it an extremely attractive option for feature selection. However, this approach is highly dependent on the calculation of the optimal cut-off value for each antibody. Therefore, small perturbations in the data might influence its calculation, which reduces the chance of obtaining the same antibody selection and classifier. Thus, reproducibility may be hindered when using this feature selection methodology across different studies. Finally, despite being statistically challenging, our parametric approach provides a more comprehensive analysis of the data. In this approach, feature selection is made on the basis of data transformation and dichotomization via mixture modelling, thus accommodating different data patterns. However, this feature selection strategy is expected to increase the computational time dramatically with as the number of antibodies under analysis increases. The computational implementation in user-friendly packages is also not trivial in relation to the other feature strategies applied in this study. Finally, this feature selection strategy is based on complex statistical models such as finite mixture models related to Skew-Normal distributions. In this scenario, this strategy seems less appealing to the malaria research community where, despite the efforts to improve mathematical modelling capacity, the availability of qualified staff with statistical and machine learning skills remains scarce. Therefore, the use of simple filter methods seems a more viable solution at the moment, especially, when it comes to analyze data featuring thousands of antibodies. Such a case is seen in Proietti et al.7 where antibodies with a p-value < 0.01 for the univariate logistic regression were selected after Bonferroni correction followed by sparse partial least squares discriminant analysis (sPLS-DA) and Support Vector Machine (SVM). Another example is the use of the Spearman’s correlation coefficient to remove highly correlated antibodies prior to implementation of the Random Forest presented by Valletta and Recker15.

A significant disadvantage of filter methods is the inability to detect complex relations between multiple features and the outcome of interest, which generally translates into pourer results in the predictive phase56,57. Thus wrappers or embedded methods are more appealing. Wrappers are created around a particular classifier and rely on the classifier’s information concerning feature relevance56,57. For this reason, the computational effort they require is usually significant, becoming unfeasible in real time when thousands of features are considered. For this reason, wrappers are often avoided, and their implementation for feature selection in malaria is scarce8. A more attractive approach are embedded methods that use the core of a classifier to establish a criterion to rank features53,56. Embedded algorithms perform feature selection during the classifier training procedure while optimizing the feature set used to achieve the best accuracy. Therefore, they are less computationally costly than wrappers while still dealing with the complex interactions between multiple features and the outcome53,56. Examples of embedded feature selection methods intending to unveil antibody immune signatures in malaria are described in the literature. Aitken et al.58 used an elastic net-regularized logistic regression for antibody selection followed by a partial least squares discriminant analysis to find a minimal set of antibodies that accurately classified the individuals under analysis. Helb et al.13 used a hierarchical criterion for feature selection, where a combination of embedded and filter methods was performed before the implementation of a Super-Learner for predicting past exposure to malaria vivax13. Here, the Least Absolute Shrinkage and Selection Operator (LASSO) regression was initially used to select one third of the responses. Then, using variable importance measures from Random Forest regression they iteratively selected the best responses which were then ranked by the p-values for the underlying Spearman’s correlation coefficient13. Although not implemented here due to the relatively small number of features, we envision that embedded feature selection approaches will be more useful in datasets in where the number of antibody responses exceeds the number of observations, as already seen in a study from Mali14. A forthcoming research study will investigate this solution and its impact on variable selection.

Alternative approaches to feature selection techniques for identifying the optimal antibody combinations for the task at hand have also been proposed10,12. These rely on simulated annealing algorithms that efficiently explore the vast space of feature combinations and thus identify the optimal feature combination solution given a fixed number of features defined by the user10. Whether this approach is preferable over feature selection techniques is an interesting research question for future work.

Concerning our predictive analysis, here we opted for the use of a SL31. The reasoning for this option relied on the fact that by combining the individual predictions of each classifier, the SL avoids the bias created by manually choosing the best-fitting model procedure and often provides better results than each individual classifier31,32. However, this was not always the case, as the Random Forest classifier alone tended to provide better predictions than the Super-Learner. Given that Random Forest is an embeeded method it performs feature selection during the classifier training procedure and thus we speculated that the removal of further features could be behind this increased performance20,59. Nevertheless, our validation analysis revealed that regardless of the strategy chosen for feature selection, nearly all features were important for classification purposes. This highlights the filter strategy’s ability to identify the most relevant features, avoiding any additional feature removal by the models embedded in the SL classifier.

However, this issue should be addressed in cases where the super SL embedded methods are implemented after a feature selection phase, such as done in Helb et al13, as further feature removal might occur without the user’s knowledge which may affect the interpretability of the results. Hence the slight decrease in the SL performance is expected to be explained by the SL attempt to correct for a possible overfitting to the data when using the Random Forest model. In this sense, these results should raise awareness concerning analysis where only the Random Forest approach is considered for predictive purposes, as it may lead to overfitting. Thus, the implementation of techniques such as the SL may provide more consensual results across the classifiers chosen for the predictive stage.

Comparing our results with the previous ones by Valletta and Recker15 revealed an increase in the prediction ability of up to 14% in the best-case scenario. This result further emphasizes the impact of feature selection prior to predictive analysis. On the one hand, this step removes antibody responses with negligible effect on clinical malaria. On the other hand, this stage decreases the number of features allowing for a more thorough feature analysis increasing the chance of finding the right transformation and dichotomization for each antibody response. Concerning the antibodies identified, we found that the antibody responses against different Merozoite Surface Proteins (MSPs) were consistently selected across the different feature selection strategies. These proteins are expressed at the parasite surface, thus, providing promising targets for malaria immunity because they are repeatedly and directly exposed to the host humoral immune system7,8. In particular, msp2 has been associated with protection from clinical malaria in many studies and even suggested as a vaccine candidate9–12. For example, msp2 has been strongly associated with protection against clinical malaria in two independent cohorts of Kenyan children13. Msp4 has also been reported to have a protective effect in Kenyan children14,16. High antibody levels against msp4 constructs have been associated with reduced morbidity in a Senegalese community17. Msp7 protection against malaria has also already been identified in the Kenyan population16,18. Moreover, panels of antibodies comprising msp7 have been associated with clinical protection against malaria in Kilifi, a rural district along the Kenyan coast14. In the same article, high antibody levels against the Erythrocyte-binding antigen-175 (eba175) antigen were also associated with protection from clinical malaria in children14 .Moreover, eba175 is associated with protection from symptomatic malaria, as demonstrated in Papua New Guinean children15. These findings corroborate the ability of our methodologies to identify relevant antibodies associated with protection to malaria. However, msp10 and h103 have not been associated with clinical malaria protection. This evidence suggests that there are antibodies associated with protection against clinical malaria that have not yet been identified. Nevertheless, further studies are necessary to validate our findings. Finally, none of our feature selection metrics selected msp1, an immune response commonly associated with malaria protection and often referred to as potential vaccine candidates. Similar findings have been reported in other studies, where msp1 has been described to show low or no associations with exposition or protection to clinical malaria13,15. These inconsistent findings further suggest the need for constructing robust feature selection strategies that could help increase reproducibility among studies. Nevertheless, one should consider the appropriateness of these feature selection strategies to identify antibodies associated with protection against clinical malaria, given that they were able to identify antibodies that have been constantly proposed for disease diagnosis.

Conclusions

Here we have implemented feature selection strategies to analyze multiple antibody data. These were developed with the idea to couple classical, traditional statistical techniques for variable selection with popular machine learning techniques for predictive analysis. Considering the transformation of each antibody data individually these strategies represent a more flexible approach to accommodate different data patterns than the one commonly described in the literature. Overall, these methodologies led to an improved classification over previous analysis based on the use of the Random Forests alone, highlighting their potential to integrate future multi-sera pipelines.

Abbreviation List

AIC
Akaike’s Information Criterion
Ama
Apical membrane antigen 1
AUC
Area Under de Curve
EBA
Erythrocyte-binding antigen
ELISA
Enzyme-linked immunosorbent assay
FDR
False discovery rate
GOF
Goodness of fitness
igG
Immunoglobulin G
LASSO
Least Absolute Shrinkage and Selection Operator
LDA
linear discriminant analysis
Log
logarithmic
LRM
Logistic regression model
MSP
Merozoite Surface Protein
MSRP
MSP7-related proteins
np
Number of Protected individuals
ns
Number of Susceptible individuals
Pf
Plasmodium falciparum
Prt
Protected
QDA
Quadratic discriminant analysis
RF
Random Forest
ROC
Receiver Operating Characteristic
rS
Spearman Correlation Coefficient
SeroTAT
serological testing and treatment
SL
super learner
sPLS-DA
Sparse partial least squares discriminant analysis
Sus
Susceptible
SVM
Support vector machine
SW
Shapiro-Wilk
χ2
Chi-square
XGB
Extreme Gradient Boosting

Declarations

Ethics approval and consent to participate

This study is based on publicly available data.

Consent for publication

Not applicable

Availability of data and materials

The datasets used and/or analyzed during the current study are available in this published article: Valletta, J. J. & Recker, M. Identification of immune signatures predictive of clinical protection from malaria. PLoS Comput Biol 13, e1005812 (2017). https://doi.org/10.1371/journal.pcbi.1005812. The R scripts generated are freely available in the following GitHub address: Immune-Stats (https://github.com/Publications/Fonseca_etal.).

Competing interests

The authors declare that they have no competing interests.

Funding

André Fonseca has a PhD fellowship by FCT – Fundação para a Ciência e Tecnologia (ref. SFRH/BD/147629/2019). André Fonseca, Clara Cordeiro and Nuno Sepúlveda are partially financed by national funds through FCT under the project UIDB/00006/2020. Nuno Sepúlveda is funded by Polish National Agency for Academic Exchange (ref. grant: PPN/ULM/2020/1/00069/U/00001).

Authors’ contributions

AF and NS designed the work; AF and MS conducted the analysis; AF and NS interpreted the data; AF, PB, CC and NS have drafted the work or substantively revised it. AF, MS, PB, CC and NS have approved the submitted version.

Data Availability

All data produced are available online at:https://doi.org/10.1371/journal.pcbi.1005812

https://doi.org/10.1371/journal.pcbi.1005812

Acknowledgements

Not applicable

Footnotes

  • In this version, we made major revisions that included restructuring the overall analysis, making the objective of the paper clearer and reframing the main ideas in a more intuitive way. Major changes included dividing the overall analysis into a feature selection step and a predictive analysis step. This way of framing the analysis provided better reasoning for the use of different approaches to select the antibodies most associated with malaria disease. Here, a new approach consisting of the use of the chi-squared test to assess associations between antibody values and protection against malaria was added as a baseline model. A preliminary approach based on the Random Forest was also added to validate previously published results. Finally, a SuperLearner was adopted for conducting the predictive analysis. In opposition to the use of different separate models, the use of a SuperLearner is less time-consuming and allows to obtain more accurate results.

Bibliography

  1. 1.↵
    Kellar KL, Kalwar RR, Dubois KA, Crouse D, Chafin WD, Kane BE. Multiplexed fluorescent bead-based immunoassays for quantitation of human cytokines in serum and culture supernatants. Cytometry. 2001;45(1):27–36. doi:10.1002/1097-0320(20010901)45:1<27::AID-CYTO1141>3.0.CO;2-I
    OpenUrlCrossRefPubMedWeb of Science
  2. 2.↵
    Tsuboi T, Takeo S, Iriko H, et al. Wheat Germ Cell-Free System-Based Production of Malaria Proteins for Discovery of Novel Vaccine Candidates. Infect Immun. 2008;76(4):1702–1708. doi:10.1128/IAI.01539-07
    OpenUrlAbstract/FREE Full Text
  3. 3.
    Ubillos I, Campo JJ, Jiménez A, Dobaño C. Development of a high-throughput flexible quantitative suspension array assay for IgG against multiple Plasmodium falciparum antigens. Malar J. 2018;17(1):216. doi:10.1186/s12936-018-2365-7
    OpenUrlCrossRef
  4. 4.↵
    Cham GK, Kurtis J, Lusingu J, Theander TG, Jensen AT, Turner L. A semi-automated multiplex high-throughput assay for measuring IgG antibodies against Plasmodium falciparum erythrocyte membrane protein 1 (PfEMP1) domains in small volumes of plasma. Malar J. 2008;7(1):108. doi:10.1186/1475-2875-7-108
    OpenUrlCrossRefPubMed
  5. 5.↵
    Kanoi BN, Takashima E, Morita M, et al. Antibody profiles to wheat germ cell-free system synthesized Plasmodium falciparum proteins correlate with protection from symptomatic malaria in Uganda. Vaccine. 2017;35(6):873–881. doi:10.1016/j.vaccine.2017.01.001
    OpenUrlCrossRef
  6. 6.↵
    Kanoi BN, Nagaoka H, White MT, et al. Global Repertoire of Human Antibodies Against Plasmodium falciparum RIFINs, SURFINs, and STEVORs in a Malaria Exposed Population. Front Immunol. 2020;11. doi:10.3389/fimmu.2020.00893
    OpenUrlCrossRef
  7. 7.↵
    Proietti C, Krause L, Trieu A, et al. Immune Signature Against Plasmodium falciparum Antigens Predicts Clinical Immunity in Distinct Malaria Endemic Communities. Molecular & Cellular Proteomics. 2020;19(1):101–113. doi:10.1074/mcp.RA118.001256
    OpenUrlAbstract/FREE Full Text
  8. 8.↵
    Osier FH, Mackinnon MJ, Crosnier C, et al. New antigens for a multicomponent blood-stage malaria vaccine. Sci Transl Med. 2014;6(247). doi:10.1126/scitranslmed.3008705
    OpenUrlAbstract/FREE Full Text
  9. 9.↵
    Osier FHA, Fegan G, Polley SD, et al. Breadth and Magnitude of Antibody Responses to Multiple Plasmodium falciparum Merozoite Antigens Are Associated with Protection from Clinical Malaria. Infect Immun. 2008;76(5):2240–2248. doi:10.1128/IAI.01585-07
    OpenUrlAbstract/FREE Full Text
  10. 10.↵
    França CT, White MT, He WQ, et al. Identification of highly-protective combinations of Plasmodium vivax recombinant proteins for vaccine development. Elife. 2017;6. doi:10.7554/eLife.28673
    OpenUrlCrossRefPubMed
  11. 11.↵
    Van den Hoogen LL, Stresman G, Présumé J, et al. Selection of Antibody Responses Associated With Plasmodium falciparum Infections in the Context of Malaria Elimination. Front Immunol. 2020;11. doi:10.3389/fimmu.2020.00928
    OpenUrlCrossRef
  12. 12.↵
    Longley RJ, White MT, Takashima E, et al. Development and validation of serological markers for detecting recent Plasmodium vivax infection. Nat Med. 2020;26(5):741–749. doi:10.1038/s41591-020-0841-4
    OpenUrlCrossRefPubMed
  13. 13.↵
    Helb DA, Tetteh KKA, Felgner PL, et al. Novel serologic biomarkers provide accurate estimates of recent Plasmodium falciparum exposure for individuals and communities. Proceedings of the National Academy of Sciences. 2015;112(32):E4438–E4447. doi:10.1073/pnas.1501705112
    OpenUrlAbstract/FREE Full Text
  14. 14.↵
    Crompton PD, Kayala MA, Traore B, et al. A prospective analysis of the Ab response to Plasmodium falciparum before and after a malaria season by protein microarray. Proceedings of the National Academy of Sciences. 2010;107(15):6958–6963. doi:10.1073/pnas.1001323107
    OpenUrlAbstract/FREE Full Text
  15. 15.↵
    Valletta JJ, Recker M. Identification of immune signatures predictive of clinical protection from malaria. PLoS Comput Biol. 2017;13(10):e1005812. doi:10.1371/journal.pcbi.1005812
    OpenUrlCrossRef
  16. 16.↵
    Van den Hoogen LL, Présumé J, Romilus I, et al. Quality control of multiplex antibody detection in samples from large-scale surveys: the example of malaria in Haiti. Sci Rep. 2020;10(1):1135. doi:10.1038/s41598-020-57876-0
    OpenUrlCrossRef
  17. 17.↵
    Wu L, Hall T, Ssewanyana I, et al. Optimisation and standardisation of a multiplex immunoassay of diverse Plasmodium falciparum antigens to assess changes in malaria transmission using sero-epidemiology. Wellcome Open Res. 2020;4:26. doi:10.12688/wellcomeopenres.14950.2
    OpenUrlCrossRefPubMed
  18. 18.↵
    Ambrosino E, Dumoulin C, Orlandi-Pradines E, et al. A multiplex assay for the simultaneous detection of antibodies against 15 Plasmodium falciparum and Anopheles gambiae saliva antigens. Malar J. 2010;9(1):317. doi:10.1186/1475-2875-9-317
    OpenUrlCrossRefPubMed
  19. 19.↵
    Breiman L. Random Forests. Mach Learn. 2001;45(1):5-32. doi:10.1023/A:1010933404324
    OpenUrlCrossRef
  20. 20.↵
    Ahmed FYH, Ali YH, Shamsuddin SM. Using K-Fold Cross Validation Proposed Models for Spikeprop Learning Enhancements. International Journal of Engineering & Technology. 2018;7(4.11):145. doi:10.14419/ijet.v7i4.11.20790
    OpenUrlCrossRef
  21. 21.↵
    Wright MN, Ziegler A. ranger : A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. J Stat Softw. 2017;77(1). doi:10.18637/jss.v077.i01
    OpenUrlCrossRef
  22. 22.↵
    Bradley AP. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997;30(7):1145–1159. doi:10.1016/S0031-3203(96)00142-2
    OpenUrlCrossRef
  23. 23.↵
    Kuhn M. caret: Classification and Regression Training. Published online 2022. Accessed May 26, 2022. https://CRAN.R-project.org/package=caret
  24. 24.↵
    Nachar N. The Mann-Whitney U: A Test for Assessing Whether Two Independent Samples Come from the Same Distribution. Tutor Quant Methods Psychol. 2008;4(1):13–20. doi:10.20982/tqmp.04.1.p013
    OpenUrlCrossRef
  25. 25.↵
    Domingues TD, Grabowska AD, Lee JS, et al. Herpesviruses Serology Distinguishes Different Subgroups of Patients From the United Kingdom Myalgic Encephalomyelitis/Chronic Fatigue Syndrome Biobank. Front Med (Lausanne). 2021;8. doi:10.3389/fmed.2021.686736
    OpenUrlCrossRef
  26. 26.↵
    Tengvall K, Huang J, Hellström C, et al. Molecular mimicry between Anoctamin 2 and Epstein-Barr virus nuclear antigen 1 associates with multiple sclerosis risk. Proceedings of the National Academy of Sciences. 2019;116(34):16955–16960. doi:10.1073/pnas.1902623116
    OpenUrlAbstract/FREE Full Text
  27. 27.↵
    Asar Ö, Ilk O, Dag O. Estimating Box-Cox power transformation parameter via goodness-of-fit tests. Commun Stat Simul Comput. 2017;46(1):91–105. doi:10.1080/03610918.2014.957839
    OpenUrlCrossRef
  28. 28.↵
    Sepúlveda N, Stresman G, White MT, Drakeley CJ. Current Mathematical Models for Analyzing Anti-Malarial Antibody Data with an Eye to Malaria Elimination and Eradication. J Immunol Res. 2015;2015:1–21. doi:10.1155/2015/738030
    OpenUrlCrossRef
  29. 29.↵
    Domingues TD, Mouriño H, Sepúlveda N. Analysis of antibody data using Finite Mixture Models based on Scale Mixtures of Skew-Normal distributions. Published online 2021. doi:10.1101/2021.03.08.21252807
    OpenUrlAbstract/FREE Full Text
  30. 30.↵
    Benjamini Y, Yekutieli D. The control of the false discovery rate in multiple testing under dependency. The Annals of Statistics. 2001;29(4). doi:10.1214/aos/1013699998
    OpenUrlCrossRef
  31. 31.↵
    Van der Laan MJ, Polley EC, Hubbard AE. Super Learner. Stat Appl Genet Mol Biol. 2007;6(1). doi:10.2202/1544-6115.1309
    OpenUrlCrossRefPubMed
  32. 32.↵
    Polley E, LeDell E, Kennedy C, Van der Laan M. SuperLearner: Super Learner Prediction. Published online 2021. Accessed March 13, 2023. https://CRAN.R-project.org/package=SuperLearner
  33. 33.↵
    Davis J, Goadrich M. The relationship between Precision-Recall and ROC curves. In: Proceedings of the 23rd International Conference on Machine Learning - ICML ’06. ACM Press; 2006:233-240. doi:10.1145/1143844.1143874
    OpenUrlCrossRef
  34. 34.↵
    Düntsch I, Gediga G. Confusion Matrices and Rough Set Data Analysis. J Phys Conf Ser. 2019;1229(1):012055. doi:10.1088/1742-6596/1229/1/012055
    OpenUrlCrossRef
  35. 35.↵
    López-Ratón M, Rodríguez-Álvarez MX, Suárez CC, Sampedro FG. OptimalCutpoints: An R Package for Selecting Optimal Cutpoints in Diagnostic Tests. J Stat Softw. 2014;61(8). doi:10.18637/jss.v061.i08
    OpenUrlCrossRef
  36. 36.↵
    Pessach D, Shmueli E. A Review on Fairness in Machine Learning. ACM Comput Surv. 2023;55(3):1–44. doi:10.1145/3494672
    OpenUrlCrossRef
  37. 37.↵
    Wang X, Zhang Y, Zhu R. A brief review on algorithmic fairness. Management System Engineering. 2022;1(1):7. doi:10.1007/s44176-022-00006-z
    OpenUrlCrossRef
  38. 38.↵
    R Core Team. R: A Language and Environment for Statistical Computing. Published online 2022. Accessed October 26, 2022. https://www.R-project.org/
  39. 39.↵
    Dag O, Ilk O. An algorithm for estimating Box–Cox transformation parameter in ANOVA. Commun Stat Simul Comput. 2017;46(8):6424–6435. doi:10.1080/03610918.2016.1204458
    OpenUrlCrossRef
  40. 40.↵
    Microsoft Corporation, Weston S. doParallel: Foreach Parallel Adaptor for the “parallel” Package. Published online 2022. Accessed March 23, 2023. https://CRAN.R-project.org/package=doParallel
  41. 41.↵
    Wickman H, François R, Henry L, Müller K. dplyr: A Grammar of Data Manipulation. Published online 2021. Accessed March 14, 2022. https://CRAN.R-project.org/package=dplyr
  42. 42.↵
    Wickham H. ggplot2: Elegant Graphics for Data Analysis. Published online 2016. Accessed March 13, 2023. https://ggplot2.tidyverse.org
  43. 43.↵
    Slowikowski K. ggrepel: Automatically Position Non-Overlapping Text Labels with “ggplot2.” Published online 2023. Accessed April 11, 2023. https://CRAN.R-project.org/package=ggrepel
  44. 44.↵
    Hothorn T, Zeileis A, Farebrother WR, et al. lmtest: Testing Linear Regression Models. Published online March 21, 2022. Accessed January 27, 2023. https://CRAN.R-project.org/doc/Rnews/
  45. 45.↵
    Venables WB, Ripley BD. Modern Applied Statistics with S. Fourth.; 2002. Accessed April 23, 2022. https://www.stats.ox.ac.uk/pub/MASS4/
  46. 46.↵
    Prates MO, Cabral CRB, Lachos VH. mixsmsn : Fitting Finite Mixture of Scale Mixture of Skew-Normal Distributions. J Stat Softw. 2013;54(12). doi:10.18637/jss.v054.i12
    OpenUrlCrossRefPubMed
  47. 47.↵
    Robin X, Turck N, Hainard A, et al. pROC: an open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinformatics. 2011;12(1):77. doi:10.1186/1471-2105-12-77
    OpenUrlCrossRefPubMed
  48. 48.↵
    Azzalini A. sn: The Skew-Normal and Related Distributions Such as the Skew-t and the SUN. Published online April 4, 2023. Accessed May 18, 2022. http://azzalini.stat.unipd.it/SN/
  49. 49.↵
    Wickham H. tidyr: Tidy Messy Data. Published online 2021. Accessed March 13, 2023. https://CRAN.R-project.org/package=tidyr
  50. 50.↵
    Boyle MJ, Reiling L, Osier FH, Fowkes FJI. Recent insights into humoral immunity targeting Plasmodium falciparum and Plasmodium vivax malaria. Int J Parasitol. 2017;47(2-3):99–104. doi:10.1016/j.ijpara.2016.06.002
    OpenUrlCrossRef
  51. 51.
    Stone WJR, Campo JJ, Ouédraogo AL, et al. Unravelling the immune signature of Plasmodium falciparum transmission-reducing immunity. Nat Commun. 2018;9(1):558. doi:10.1038/s41467-017-02646-2
    OpenUrlCrossRef
  52. 52.↵
    Oulton T, Obiero J, Rodriguez I, et al. Plasmodium falciparum serology: A comparison of two protein production methods for analysis of antibody responses by protein microarray. PLoS One. 2022;17(8):e0273106. doi:10.1371/journal.pone.0273106
    OpenUrlCrossRef
  53. 53.↵
    Bolón-Canedo V, Sánchez-Maroño N, Alonso-Betanzos A, Benítez JM, Herrera F. A review of microarray datasets and applied feature selection methods. Inf Sci (N Y). 2014;282:111-135. doi:10.1016/j.ins.2014.05.042
    OpenUrlCrossRef
  54. 54.↵
    Ruiz R, Riquelme JC, Aguilar-Ruiz JS. Incremental wrapper-based gene selection from microarray data for cancer classification. Pattern Recognit. 2006;39(12):2383–2392. doi:10.1016/j.patcog.2005.11.001
    OpenUrlCrossRefWeb of Science
  55. 55.↵
    Piatetsky-Shapiro G, Tamayo P. Microarray data mining. ACM SIGKDD Explorations Newsletter. 2003;5(2):1–5. doi:10.1145/980972.980974
    OpenUrlCrossRef
  56. 56.↵
    Saeys Y, Inza I, Larrañaga P. A review of feature selection techniques in bioinformatics. Bioinformatics. 2007;23(19):2507–2517. doi:10.1093/bioinformatics/btm344
    OpenUrlCrossRefPubMedWeb of Science
  57. 57.↵
    Inza I, Larrañaga P, Blanco R, Cerrolaza AJ. Filter versus wrapper gene selection approaches in DNA microarray domains. Artif Intell Med. 2004;31(2):91–103. doi:10.1016/j.artmed.2004.01.007
    OpenUrlCrossRefPubMedWeb of Science
  58. 58.↵
    Aitken EH, Damelang T, Ortega-Pajares A, et al. Developing a multivariate prediction model of antibody features associated with protection of malaria-infected pregnant women from placental malaria. Elife. 2021;10. doi:10.7554/eLife.65776
    OpenUrlCrossRef
  59. 59.↵
    Loecher M. Unbiased variable importance for random forests. Commun Stat Theory Methods. 2022;51(5):1413–1425. doi:10.1080/03610926.2020.1764042
    OpenUrlCrossRef
Back to top
Posted September 05, 2023.
Download PDF
Data/Code
Email
Antibody selection strategies and their impact in the analysis of malaria multi-sera data
André Fonseca, Mikolaj Spytek, Przemyslaw Biecek, Clara Cordeiro, Nuno Sepúlveda
medRxiv 2022.10.06.22280719; doi: https://doi.org/10.1101/2022.10.06.22280719
Twitter logo Facebook logo LinkedIn logo Mendeley logo
Citation Tools

Subject Area