Abstract
Background Compartmental infectious disease (ID) models are often used to evaluate non-pharmaceutical interventions (NPIs) and vaccines. Such models rarely separate within-household and community transmission, potentially introducing biases. We formulated an approach that incorporates household structure into ID models, extending the work of House and Keeling.
Design We developed a multi-compartment susceptible-exposed-infectious-recovered-susceptible-vaccinated (MC-SEIRSV) modeling framework, allowing non-exponentially distributed duration in Exposed and Infectious compartments, that tracks within-household and community transmission. We simulated epidemics that varied systematically by community and household transmission rates, waning immunity rate, household size (3 or 5 members), and numbers of Exposed and Infectious compartments (1-3 each). We calibrated otherwise identical models without household structure to the early phase of each parameter combination’s epidemic curve. We compared each model pair in terms of epidemic forecasts and predicted NPI and vaccine impacts on: the timing and magnitude of the epidemic peak and on its total size. Meta-analytic regressions characterized the relationship between household structure inclusion and the size and direction of biases.
Results Otherwise similar models with and without household structure produced equivalent early epidemic curves. However, forecasts from models without household structure were biased. Without intervention, they were upward-biased on peak size and total epidemic size, with biases also depending on the number of Exposed and Infectious compartments. Model-estimated NPI effects of a 60% reduction in community contacts on peak time and size were systematically overestimated without household structure. When the NPI yielded a 20% reduction, biases were smaller. Because vaccination impacted both community and household transmission, their biases were still smaller.
Conclusions ID models without household structure can produce biased outcomes. Analysts should consider incorporating household structure.
1 Introduction
Compartmental infectious-disease (ID) dynamic transmission models are often used to quantify the magnitude and timing of benefits from non-pharmaceutical interventions (NPIs) and vaccines for mitigating and controlling respiratory infectious diseases. However, they may fail to provide accurate epidemic forecasts or estimates of real-world policy effects due to simplifications they necessarily make. In particular, compartmental models often simplify mixing and transmission patterns, rarely separating transmission within households from community transmission. While dynamic transmission microsimulation models with explicit contact networks avoid such simplifications, they can be highly computationally intensive, especially when used to model large populations. They also require extensive data to parameterize their realistic contact networks or assumptions about how contacts form and dissolve.
As a feasible alternative, past work has described approaches for explicitly incorporating household transmission into compartmental Susceptible-Infected-Recovered (SIR) models [HK08]. In SIR models, household size and transmission affect the dynamics of outbreaks, including the growth rate of infections [HK09]. Prior studies show that including household transmission in SIR models can alter the time course and level of the overall epidemic when the pace of household transmission differs from that of community transmission. The magnitude of these differences depends on the number of people living in each household (i.e., household size). Furthermore, the effects of NPIs predicted with a SIR model that does not separately model household transmission could differ if, for example, an NPI (e.g., business closures) reduced community transmission differently than household transmission.
The utility of past work incorporating household transmission into SIR models would be substantially increased if the approach could be used for more complex compartmental models. Sometimes it is necessary for realism to implement multi-compartment Susceptible-Exposed-Infected-Recovered (SEIR) models of open populations and to include symptomatic infections, case detection, venue-specific transmission, and combinations of NPIs and vaccination [KR08]. For example, when the Mexico City Metropolitan Area (MCMA) faced risks of COVID-19 outbreaks, using a network microsimulation model of its population of almost 20 million would not have been feasible, but the compartmental model used for this epidemic required many of these characteristics [Ala+21].
In this manuscript, we extend the mathematical framework of a model of household and community transmission based on House and Keeling’s work to include more complex compartmental models and a suite of interventions. We illustrate the relevance of these extensions by showing how failure to incorporate household transmission into more complex compartmental models can bias epidemic predictions and intervention effects in terms of overall epidemic magnitude and the timing and height of the epidemic peak. Further, we characterize the systematic ways this exclusion biases these outcomes and depends on household size in conjunction with other model features.
2 Mathematical Framework for Community and Household Models
2.1 SIR to MC-SEIRSV with Interventions
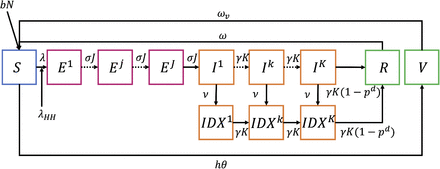
The epidemiology of many IDs can be described as a multi-compartment susceptible-exposed-infectedrecovered-susceptible-vaccinated (MC-SEIRSV) model with demography [KR08]. In such a model, the exposed (E) compartments represent individuals that are infected but who are not yet infectious, and the infectious (I) compartments represent individuals that are both infected and infectious (i.e., can infect susceptibles (S) if contact occurs) [KR08]. Notably, by using multiple levels for the E and I compartments and allowing for differential rates of symptom onset and detection (described in sections below), the model structure can also capture the possibility of asymptomatic infectiousness as well as infectiousness varying over the course of infection. Figure 1 depicts the generalized structure of the MC-SEIRSV compartmental model. Each of these compartments represents part of the population characterized by their disease, diagnostic, and vaccination status as a function of time.
Model diagram.
The full model represents multiple disease, demographic, and intervention processes. In the model, people are born into the susceptible compartment S at a rate b and face a background mortality rate (μ) from all compartments (mortality not shown in the figure). People can become infected at a rate λ and enter the exposed compartment, E, progressing to becoming infectious and moving to I before recovering and entering R. We stratified the infectious compartments by whether or not people have been diagnosed (DX). Those who are infected face an excess risk of death from their infections (pd), which may be reduced by proper and timely medical therapies. Those who recover may lose their immunity at a rate ω and return to the susceptible compartment. We ensure realistic distributions of times in E and I by using a multicompartment structure. Specifically, we have multiple E and I compartments and rates of progression (σ) from E to I and (γ) from I to R that are multiplied by the number of each type of compartment (J and K, respectively) [KR08]. Health states with a multi-compartment structure (e.g., E and I) have nonexponentially distributed dwell times (NEDT) following an Erlang distribution. In contrast, if there are only single compartments, they would have exponentially distributed dwell times (EDT) [KR08]. The total size of the population at time t is Pop, which is the sum across compartments and all other stratifications noted above.
To appropriately capture the dynamics of many infectious disease epidemics, including COVID-19, it is important to consider household transmission, as well as community transmission[Pel+20]. We term the model’s components described until now the “community submodel” (i.e., the non-household components) to differentiate them from the “household submodel”, which we describe in detail below.
In brief, the household submodel acknowledges that people are generally embedded within households. The embedding implies that: 1) once a given household’s members are all infected and/or recovered, no further transmission occurs within that household (unless immunity wanes or there are births/entries into the household); and 2) if households are not entirely isolated from one another such that community transmission is still occurring, then the interaction between the susceptible and infectious individuals within the household can drive additional community transmission via the within-household force of infection,, λHH, (related to the household secondary attack rate, e.g., [Fun+20])a component of the overall force of infection. These household embeddings are also essential when interventions (e.g., shelter-in-place) differentially impact community transmission and household transmission, such as masking or social distancing measures that apply to communal spaces but not households. By extending the prior approach in [HK08] and combining it with our community submodel (the MC-SEIRSV model), we produce an overall population model.
To describe overall transmission dynamics in the population, we first describe transmission in the community submodel, then the key elements of the household submodel, and how the household submodel’s transmission is integrated into the community submodel.
2.2 Community submodel with transmission from the household force of infection
The community MC-SEIRSV model is described by a system of ordinary differential equations (ODEs) (see Appendix A.1.1).
2.2.1 Force of infection
The force of infection (FOI) is the key quantity governing the transmission of infection within a given population, defined as the instantaneous per-capita rate at which susceptibles acquire infection. FOI reflects both the degree of contact between susceptibles and infectious individuals and the pathogen’s transmissibility per contact. Because contacts can occur both in the community and within a household and because particular interventions (e.g., NPIs) may differentially reduce such contacts, we construct non-householdand household-specific FOIs. The community FOI, λ, represents the rate of disease transmission from infectious people in the community (see Appendix A.1.2); we likewise define the household FOI,, \HH, described below.
2.2.2 Interventions that impact the force of infection
The model also incorporates two epidemic control interventions: NPIs and vaccination. NPIs reduce the community FOI by a value ϕ ∈ [0, 1]. Susceptible individuals are vaccinated at a rate h in whom a proportion, θ ∈ [0, 1], will be effectively immunized. Successfully vaccinated individuals, like recovered individuals, cannot be infected until their immunity wanes at a rate ωv.
2.3 Household submodel
As with [HK08], the household submodel tracks the proportion of households whose members are in various states of the disease’s natural history. For example, in a given population at a given time, 5% of all 3-person households might have 1 member susceptible and 2 members recovered (HH(S=1,…,R=2)). More generally, we denote the proportion of households whose members are in any combination of community MC-SEIRSV model states (i.e., counts of members in each state which we abbreviate sc for state counts) as HHsc, where ∑sc HHsc = 1.
The number of distinct HHsc’s that represent households with different state counts grows with both household size (hhsize) and with the number of states in the community model (states). The equation for the number of household proportions (and hence number of differential equations in the household submodel) with a fixed household size is:
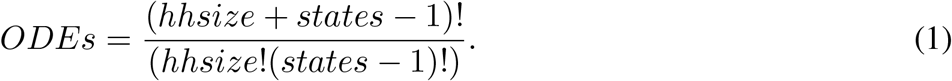
To keep the number of household types, and hence ODEs in the household submodel, manageable, we assume that all households are the same size as the average household for a given location, rounding the average household size to the nearest whole integer (e.g., hhsize =3 for Mexico City Metropolitan Area, Mexico).
We ensure that the household submodel’s initial state is consistent with the community submodel’s initial state. For a given size of the total population at the start of the community model P opt=0 under the assumption of all households being size hhsize = hhsizeavg, the number of households is Nhouseholds = Popt=0/hhsizeavg. If there is one person in the E1 state in the entire population, then the fraction of households that have an infected member is 1/Nhouseholds and the remainder are households with all susceptibles: (Nhouseholds -1)/Nhouseholds. For other starting conditions (i.e., more than one exposed, infectious, or recovered individual), this initialization generalizes easily under the assumption that the households in which the initial few infections occur are not correlated (i.e., if there are 3 infections, they occur in 3 separate households because Nhouseholds is much larger than the initial number of infections). This assumption can be relaxed without loss of generality.
The household submodel’s dynamics include: progression, recovery, waning immunity, vaccination, within-household and community-household transmission, births, and deaths. Modeling many of these dynamics in the household submodel is somewhat more complicated than in the community submodel because the household submodel tracks the fraction of households in a set of discrete states characterized by counts of members in each community MC-SEIRSV model state and hence has multiple exposed and infectious compartments relevant for progression and recovery.
The following examples provide the intuition of how the household submodel handles progression and recovery.
In a simplified example ignoring the multi-compartment nature of the exposed and infectious states and considering only progression, if there are 4 household members (1 susceptible, 3 exposed, 0 infectious) at a given time, then it is possible that 0, 1, 2, or all 3 of the exposed members will progress to infectious on a given day. Hence, the possible states that this household could be in on the next day include: (1 susceptible, 3 exposed, 0 infectious); (1 susceptible, 2 exposed, 1 infectious); (1 susceptible, 1 exposed, 2 infectious); or (1 susceptible, 0 exposed, 3 infectious). In the example, the frequency of households moving to each state follows a binomial distribution with the probability related to the rate of progression (o). When considering multiple exposed and infectious compartments in the community MC-SEIRSV model, the binomial distribution’s probability is then related to σJ. And if there are household members in several of the multi-compartment exposed states, the general form of these resulting frequencies of household states follows a convolution of binomial distributions. The case for recovery follows a similar pattern where, in the multi-compartment model, the frequencies of resulting household states also follow a convolution of binomial distributions with probability related to γK.
In general, in models of counts of household members where E and/or I are multi-compartment, the counts of household members that progress and/or recover, follow a convolution of binomial distributions. The details of this calculation are as follows. Consider C individuals (i.e., the members of a household) each in a Markov chain with states 
for c ∈ {1,…, C}. The M states in our case are those in the community MC-SEIRSV model. The Markov chain has the following transition probabilities (where for simplicity, we have set the probability of flow from R to S equal to 0, i.e., no waning immunity):
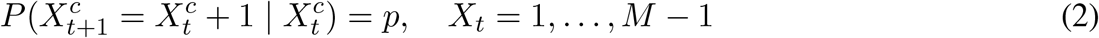
In other words, for all states except the last, with probability p, each individual progresses from Xt to Xt+1 (e.g., E2 to E3 or from E3 to I1) and with probability 1− p the individual stays in the same state. Individuals remain with certainty in the last (Mth) state after progressing to it.
Having considered each individual, we now consider counts of household members. Let 
be the number of individuals in state m at time t. We consider a new Markov chain with state 
. The transition probabilities for the counts of household members can be calculated as follows. Given a transition from state 
to state 
:
For each of the M −1 transition arcs in the underlying Markov chain, find the number of individuals transitioning from state m to m + 1, denoted Δt(m, m + 1) for m< M.
The probability of the transition is then a (convolution of) binomial distribution(s):
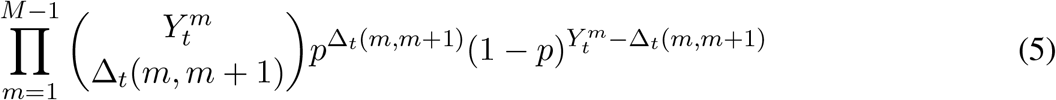
To find the value of Δt(m, m + 1), use the following backwards recursion:
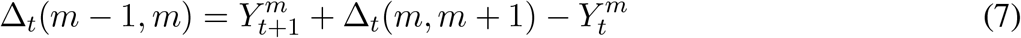
In other words, for each source state (e.g., E2) which at time t might have h household members in it, 0, 1, …, h members may progress to E3 at time t +1 with the rest remaining in E2. The counts of progressors are binomially distributed. However, if there are also some household members in E3 at time t, then the count of people in E3 at time t +1 is more complicated because it depends on the count of the progressors from E2 as well as the count of the non-progressors among those in E3. Hence, we arrive at a convolution of binomial distributions as the general description provided in equation (5) with a simple binomial distribution for cases where individuals are in one source state and none in the destination state at time t. Likewise, waning immunity follows what we have just described for progression and recovery.
2.3.1 Household force of infection
There are both within-household and community-household transmission routes in the household submodel. Within-household transmission involves infectious household members infecting susceptible household members. Community-household transmission involves infectious individuals in the community (people who are not household members) infecting susceptible household members.
Within-household transmission is related to three components: a) the current number of infectious household members; b) the rate of contact between household members; c) the probability of withinhousehold transmission given household contacts (τ). The number of infectious individuals in the household is given directly by the household compartment being considered (HHsc). The number of implied daily household contacts for a particular jurisdiction can be computed from household mixing matrices such as those published by Mossong et al., [Mos+08]. Finally, note that because the intensity of household contacts may differ from contacts in the community, the probability of transmission conditional on household contacts (τ) differs from the probability of transmission given community contacts (β).
The household FOI, λHH, is therefore defined separately from the community FOI, λ, and connects the dynamics of the household submodel back to the community submodel. λHH depends on the number of within-household contacts between susceptible and infectious members and the probability of transmission given a household contact (τ). In the community submodel, when infectious individuals are detected, their probability of transmission, β, is reduced by a factor f ∈ [0, 1]. So too, in the household submodel, τ is scaled by the same constant yielding τ′. However, a necessary simplification for scaling τ to produce τ′ is that the fraction of household infectious contacts to which this scaling factor applies is assumed to be the same as the fraction of prevalent infectious individuals who are currently detected in the community submodel. Therefore, within each household, we define the rate of new infections as infection as
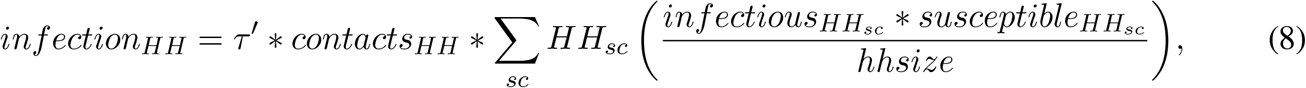which is the weighted average of within-household transmission (higher where there are more infectious and susceptible individuals simultaneously present in the household), where the weight is the fraction of households with these counts of infectious and susceptible members. The infections generated by household transmission, infectionHH, are then used to increase the flow of new infections from S to E as tracked in the community submodel, producing λHH referenced above.
2.3.2 Births and Deaths
Like the community submodel, the household submodel includes birth and deaths. Because the household submodels tracks proportions, it makes the simplifying assumption that births equal deaths so that its proportions always sum to 1, ∑sc HHsc = 1, and that at any given time, the fraction of incident deaths due to disease is relatively small. Hence, it exposes all households to an average background mortality rate, determining the birth rate. Births are spread proportionally across only household compartments with at least one susceptible member (i.e., newly born individuals are assumed to be born susceptible). In principle, this assumption could be relaxed if transmission occurred in utero or at birth (e.g., vertical transmission of HIV).
3 Simulations and analyses
To illustrate the value of our community-household modeling framework, we analyze its predictions compared to models that only include community transmission. Specifically, we perform analyses to assess how failure to include household transmission in more complex compartmental models can bias both predictions of epidemic outcomes and intervention effects. Outcomes include the cumulative epidemic magnitude along with the timing and height of epidemic peaks and how these are changed through interventions. We characterize systematic relationships between the size and direction of outcome biases and the population’s average household size in conjunction with other model features and parameters. We employ a design-ofexperiments approach, simulating outcomes across a range of household sizes, numbers of exposed and infectious compartments, transmission and recovery patterns, and in the presence/absence of various interventions. We use a meta-analytic regression approach to characterize the general patterns of bias estimated over the model simulations.
3.1 Interventions
We employ a set of stylized interventions to probe biases in how models that do or do not include household transmission estimate their effects. We consider higher and lower levels of contact reductions via NPIs and different levels of vaccine coverage and vaccine effectiveness. NPI effectiveness (ϕ) reduces community contacts by 20% or 60%. Vaccine coverage (h) is 30% or 90%, and vaccine effectiveness (θ) is 50% or 90%. As public health responses take some time, we initiated interventions 10 days after the start of the model, roughly at a point where the 50% interquantile range of the number of detected cases was between 8 and 115 infections per 100,000 across the different combinations of model parameter values in the absence of interventions.
3.2 Outcomes
We focused on three outcomes, O, generated by the model: epidemic size, defined as the integral of the prevalent infection epidemic curve; epidemic peak, defined as the maximum number of prevalent infections on a given day; and time when the epidemic peak occurs (see Appendix A.1.3).
3.3 Control measures’ effectiveness
We analyzed the outcomes and the effects of control measures on them. We define each control measure’s effectiveness (ΔO) as the difference in outcome with no control measure (Onc) and the outcome with the control measure (Oc), given by
In general, control measures reduce the number of cases; hence, ΔO will tend to be a larger positive quantity for more effective control measures. Control measures also generally delay the epidemic peak, so for this outcome, ΔO will tend to be a larger negative quantity for more effective control measures.
3.4 Calibration for bias assessment
We evaluated how failure to include household size and other features in the model produced bias in model outcomes and estimated control measure effects. We sought to enable an interpretable comparison of otherwise similar models that only differ by their inclusions/exclusion of household transmission. Specifically, we imagined an analyst in the early days of an epidemic deciding whether to include household transmission in a dynamic model to be used for epidemic forecasting and consideration of interventions and their potential effects. If the truth is that household transmission occurs and hence household structure should be included, how much and what kinds of biases occur in modeled outcomes if household transmission is omitted?
Hence, for each combination of the number of exposed compartments, the number of infectious compartments, household sizes greater than 1 (i.e., models with household structure), household transmission rate, community rate, and waning rate shown in Table A1, we generated an epidemic trace of incident daily infections for the first 15 days of the epidemic in the absence of interventions. For each combination, we then instantiated a corresponding model with the same parameters except that it had no household transmission (τ = 0 and household size of 1) and calibrated its community transmission parameter (β) such that the model without household transmission produced daily incident infections in the first 15 days that matched the model with household transmission. Since we were considering a deterministic case without uncertainty, we were only interested in capturing point estimates of /β to match outcomes to the model with household transmission. As such, we used the Nelder-Mead algorithm for calibration and minimized the sum of squared errors between the models’ daily incidence (with household transmission vs. no household transmission).
We used the corresponding pairs of models (those with and without household transmission that have the same epidemic trace for the first 15 days) to assess how predicted outcomes and intervention effects might be biased.
We quantified the bias as the absolute or percentage change in a given control measure’s effectiveness as predicted with a model that includes both community and household transmission (HH) versus as predicted with the corresponding model that only includes community transmission but produced the same first 15-day epidemic trace (NH). The absolute bias (aBias) is defined as
and the relative bias (rBias) is
If the effect of an intervention is a reduction in an outcome (e.g., total infection days, peak infections, etc.), then an absolute positive bias implies that the estimated effectiveness of control measures is smaller when household transmission is not included (i.e., underestimated effectiveness). If the effect of an intervention is to increase an outcome (e.g., life expectancy, time to epidemic peak, etc.), then an absolute positive bias implies that the estimated effectiveness is larger when household transmission is not included (overestimated effectiveness).
3.5 Design of experiments
We used a meta-analytic regression approach to relate epidemic outcomes and biases to the household size, numbers of exposed and infectious compartments, and community and household transmission rates. The regressions also included two-way interactions between household size and the number of exposed and infectious compartments to allow for non-linear relationships.
For the epidemic outcomes in the absence of intervention, we performed the regressions for each outcome based on a set of parameter values generated following a full factorial design of experiments (DoE) (Table A1).[HKP17; MWC19]
For intervention effects, we used the same general approach in terms of a DoE design and metaregression. We focused on intervention effects of NPIs that would be differentially delivered in communities vs. households (e.g., business closures or physical distancing) in the absence of vaccination. In supplementary analyses, we considered vaccination in the absence of NPIs.
4 Results
4.1 Household structure and calibrated model parameter values
Otherwise similar models with and without household structure can produce equivalent early epidemic curves across a broad range of disease parameters. However, this does not guarantee that their longerterm epidemic projections or projected intervention effects will be similar. With otherwise similar modeling choices at the beginning of an outbreak, models that do not include household structure calibrated to the initial period’s rise in infection prevalence correspond closely to otherwise similar models with a household structure for the 648 natural history parameter combinations in our study. Calibration of all models lacking a household structure converged and produced epidemic curves whose daily number of prevalent infections differed from corresponding models with household structure by 1% on average and (all less than 2.25%). For all parameter combinations, calibration of the models without household transmission yielded higher community transmission rates (β) than corresponding models that include a household structure to offset household transmission (τ) that they did not include. On average, β in the models without household structure was 0.23 higher than in corresponding models with household structure. Meta-analytic regressions revealed that calibrated /3s for models without household structure were significantly higher when either β or τ in the corresponding model with a household structure was higher, and even more so for models with larger household sizes and when the exposed states have NEDT (i.e., models with more E compartments) (Appendix Table A2).
4.2 Impact on model-predicted, longer-term natural history
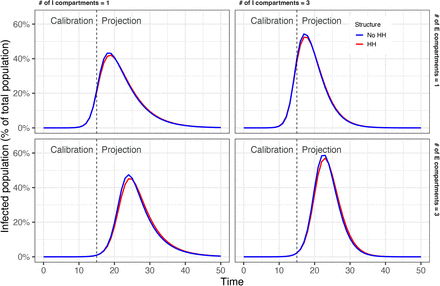
Failure to include household structure can cause modeled longer-term epidemic natural history to differ from otherwise similar models across a broad range of disease parameters. Figure 2 shows the natural history epidemic curves for an exemplar set of parameters for which we systematically varied the number of exposed and infectious states. For this example where a household size of 3 is used, when the household structure is not included, the model’s epidemic curve peaks earlier and higher and drops sooner compared to the model that includes household transmission, and the differences appear slightly larger when the exposed states have NEDT (i.e., there are multiple E compartments). More generally, Appendix Tables A3 A4 show that failure to include household structure when projecting the epidemic natural history results in higher peak infections on average with slightly higher variation across parameters sets and also slightly higher cumulative infections with slightly lower variance.
Natural history epidemic curves.
Using meta-analytic regressions to examine outcomes in the absence of intervention, we found that, on average, excluding household structure did not have a significant effect on peak time. However, the trend was towards having slightly later peaks with larger household sizes. The epidemic peak was approximately 25,000 people larger (5% larger than the epidemic peak size) when the household structure was excluded for a setting with a true household size of 3 or 5. The total epidemic size over 100 days was approximately 60,000 larger (1.2% larger than the total epidemic size) when the household structure was excluded, and the true household size was 3 (approximately 57,000 larger (1.1% larger) if the true household size was 5) (Table 1). The magnitude of the differences, particularly for peak size, varied slightly when exposed and infectious states were NEDT (i.e., depending on the number of exposed and infectious states) – the more E and I compartments the greater the overestimate of the peak in an otherwise similar model without household structure compared to one with household structure.
Meta-regression estimates on absolute differences in outcomes of excluding household structure in the absence of intervention
4.3 Impact on model-predicted NPI effects
Failure to include household structure results in substantial biases in model-estimated effects of NPIs, which interact in complex ways with models that have NEDT exposed and infectious states (Appendix Tables A5 - A6). Panel A of Figure 3 shows how, in this example, the model-estimated reduction in peak size due to NPIs without household structure (ΔONH) is 32,900 larger than the model-estimated reduction with a household size of three (ΔOHH).
Control measures’ bias. Panel A shows bias with and without household structure for an NPI with 60% effectiveness in reducing community contacts
Using meta-analytic regressions, we found that, on average, model-estimated NPI effects of a 60% reduction in community contacts on peak time and peak size are systematically overestimated when the household structure is not included. In our example, the model without a household structure, the peak is more delayed by the NPI (approximately 4 days more delayed) than the delay on the peak time in an otherwise similar model with a household structure. The bias on peak time is slightly smaller when the true average household size is larger. The bias on peak size reduction due to the NPI is larger when the true household size is larger (preventing approximately 44,000 more cases at the peak without household structure when the true household size is 3; preventing approximately 45,000 more cases when the true household size is 5). For overall epidemic size over 100 days, exclusion of household structure results in an underestimate of the effect of an NPI that reduces community contacts by 60% (approximately 61,000 and 57,000 fewer cases prevented in the first 100 days when the true model’s household size is 3 and 5 respectively) (Table 2). Because models without household structure estimate that NPIs delay peaks more and push the peak size lower, the effect on the epidemic size over 100 days appear smaller because it will take longer for the epidemic to essentially die out – the key is that the dynamics are different with interventions in the model with and without household structure included. Panel B of Figure 3 illustrates this for exemplar parameter sets, showing that the model-estimated effects of NPIs on reducing peak size are frequently overestimated for NPI effectiveness of 60%, though particular combinations of household size and NEDT exposed and infectious states interact in complex ways in terms of determining the magnitude of this bias.
Meta-regression estimates on absolute bias of treatment effects, NPI = 60%
As the NPI less effectively reduces community contacts (e.g., NPI effectiveness of 20%), the biases described above tend towards being smaller and non-significant or even to underestimation of the reductions in peak size using the exemplar parameter sets (Panel B of Figure 3 and Appendix Figure 4). Using meta-analytic regressions, we found that on average, model estimated NPI effects of a 20% reduction in community contacts on impacting peak time and peak size are no longer significantly biased. For these outcomes as well as the bias in the effect on total epidemic size, which is still significant, the magnitudes of these point estimates of the biases are smaller (tending towards 0) compared to the size of the biases for a 60% effective NPI) (Appendix Table A7).
The NPI results presented thus far are for models where there is no waning immunity (ω = 0.00). Considering analyses of intervention effect bias for (ω = 0.01 or ω = 0.02) for 60% NPI effectiveness in reducing community contacts, we find that for the case of ω = 0.01 biases on peak time and peak size are only slightly larger than for the case of ω = 0.00. For overall epidemic size within 100 days, the bias appears much larger (approximately 600,000 vs. 60,000 total fewer cases averted for models without household structure) when ω = 0.01 compared to when ω = 0.00. This is a combination of many more cases occurring because waning immunity permits those with prior infection become susceptible again and changes in the timing of both the epidemic peak and when the endemic equilibrium is reached (Appendix Table A8). For ω = 0.02, biases on peak time and peak size are slightly smaller than for the case of ω = 0.00 but generally similar and still in the same direction. However, for total epidemic size, the direction of bias has now changed (approximately -550,000 vs. 60,000 total fewer cases averted for models without household structure) – with ω = 0.02, the model without household structure overestimates the reduction in total cases within 100 days (Appendix Table A9).
4.4 Impact on model-predicted vaccination effects
Biases from excluding household transmission in the estimates of NPIs’ effects on epidemic outcomes are often larger than the biases in the estimates of effects of vaccines because the modeled NPIs only impact community transmission, whereas vaccination impacts both community and household transmission (Appendix Tables A5 - A6). Appendix Figures 5 and 6 show examples of how vaccines with given effectiveness and coverage produce different epidemic curves with and without including household transmission holding all other model parameters fixed. For this example, the effect on peak size and timing is smaller for models with realistic household sizes and leads to less bias than in estimates with NPI effects (Appendix Figure 8 compared to Figure 3). More generally, we see that estimated effects on our outcomes of low coverage and low effectiveness vaccine from models without household structure compared to those otherwise similar models with household structure yields no statistically significant or large bias on expectation (Appendix Table A10). With a low coverage but high effectiveness vaccine, the findings are similar, though, for peak size, the model without household structure may underestimate the effect of the vaccine by approximately 9,000 compared to otherwise similar models with household structure (Appendix Table A11). However, for high-effective vaccine strategies at low or high coverage, different patterns of bias emerge due to models with and without household structure having different thresholds for elimination (Appendix Tables A12 and A13). Estimated delays on peak times are significantly smaller from models without household structure compared to those with household structure when vaccine coverage is lower but no longer significant with higher vaccine coverage. For peak time, models without household structure significantly underestimate reductions with lower vaccine coverage (approximately 16,000) but significantly overestimate reductions with higher coverage (approximately 17,000). For low and high coverage, reductions in total epidemic size are overestimated in models without household structure compared to those with household structure.
5 Discussion
Transmission dynamic models are important tools to support policymakers, providing forecasts of the time course of an epidemic and assessing the effectiveness of a range of control measures. While compartmental transmission dynamic models yield important insights, their simplifying assumptions regarding mixing and transmission patterns can induce biases in epidemic forecasts and estimates of intervention effectiveness. On the other hand, dynamic transmission microsimulation models may require too much-unobserved data (e.g., network structure and change over time) and computational resources to provide timely forecasts and estimates. Our study provides a feasible alternative that can address simulation needs within the spectrum of complexity from simple compartmental models to dynamic transmission microsimulation models. Specifically, it extends previous work on incorporating household transmission into simple compartmental SIR models [HK08; HK09] to include multi-compartment SEIR models that can include both NPIs that reduce community transmission and vaccination that reduces both community and household transmission.
We demonstrate the value of our modeling framework by comparing simulation results using the framework that incorporates household transmission to simulation results in which household transmission is omitted. Across a range of parameters representing diverse pathogens in many epidemiological and social situations, we show that failure to include household transmission in the model induces bias in its forecasts, particularly with regard to the size of the epidemic peak. Likewise, we show that failure to include household transmission also biases estimates of NPI effects on the epidemic outcomes in complex ways. Furthermore, biases in estimates of NPI effects in models that fail to include household transmission differ in substantial and systematic ways from biases in estimates of vaccine effects.
Failure to include household structure not only induces impacts and biases on the modeled overall course of an epidemic and the effects of interventions delivered differentially in community settings. It also limits the ability of the model to evaluate household-specific interventions in a convincing way. For example, contact investigations could be examined by increasing the rate of detection (and treatment or prophylaxis) among household contacts. Hence, our approach to inclusion of household structure across a range of compartmental models, provides additional advantages in terms of the types of targeted interventions that can be evaluated.
As noted, our modeling framework falls within a complexity spectrum between compartmental and microsimulation models. To track households and household transmission, it introduces a set of differential equations whose size grows with the number of states of the disease being modeled, any states required for the interventions considered, and the household size. Furthermore, to keep the problem tractable, it assumes that all households are of the same size – the average household size of the population. Relaxing this assumption would add even more equations to the household subcomponent of the model. Solving large systems of ordinary differential equations eventually results in numerical imprecision for compartments with extremely small proportions of the population. It can also require very long computation times. In the context of the R implementation we provide, household sizes of more than 5 combined with multi-compartments of more than 4 exposed states and more than 4 infectious states can lead to relatively long computation times (e.g., minutes to hours). Re-implementing the underlying equations in a lower-level high-performance language like C++ or a performance-optimized language like Julia and using appropriate differential equation solvers would likely raise these limits considerably. However, regardless of implementation, at some point of complexity, dynamic microsimulation models would be preferable.
As famously noted, “all models are wrong, but some models are useful” [Box76]; the goal of this study is to extend the usefulness of compartmental dynamic transmission models for forecasting and policy evaluation by developing methods to incorporate household transmission into a broad class of such models. We provide the full mathematical details of such an approach and show that it is feasible and bias-reducing to incorporate such dynamics into many such models. We believe that it is advisable to incorporate household transmission into a wide range of dynamic transmission models.
Data Availability
All data produced in the present study are available upon reasonable request to the authors
