A Formal Model for the Representation of Binary Temporal Relations in Healthcare Applications and an Efficient Algorithm for Logic-Based Temporal Subsumption Testing and Pattern Matching

1.1 Previous Work

Substantial past work has explored the representation of temporal relationships between pairs of events and reasoning over such relationships, such as the matching of temporal relationship to time-stamped data or the comparison of temporal relationships to each other. Allen’s seminal work [1] identified a complete set of 13 qualitative relations between pairs of temporal intervals, such as “precedes”,

“during”, and “overlaps”, and specified a calculus for inferring new relations based on asserted temporal facts. Although influential in subsequent research, Allen’s model did not support the representation of quantitative (metric) relationships between temporal intervals (such as “Interval A precedes Interval B by at least 24 hours, but by less than 1 week”), nor did it propose any mechanisms for evaluating temporal intervals with respect to instance data (such as “find all patients in whom a vaccination preceded a severe allergic reaction by at least 24 hours, but by less than 1 week”).

Subsequent researchers [2] modeled metric temporal relationships between time points as linear inequalities of the form “t₂ – t₁ ≥ n”, which denotes that timepoint 1 precedes timepoint 2 by at least n time units. Conjunctions of such linear inequalities allowed the representation temporal relationships that include ranges, such as “t₂ – t₁ ≥ 24 hours ^ t₂ – t₁ < 1 week. Permitting the values 0 and ∞ as constants in such expressions further extended their expressiveness, allowing the metric representation of quantitative or qualitative relationships (such as Allen’s original qualitative relations) [3,4]. For example, the semantics of the Allen interval relation “Interval 1 precedes Interval 2” could be represented as the conjunction “b₂ – e₁ > 0 ^ b₂ – e₁ < ∞”, where “b₂” denotes the beginning time point of Interval 2 and “e₁” denotes the ending time point of Interval 1.

Research on automated reasoning over such metric representations primarily addressed two tasks. First, as with Allen’s work, algorithms were developed to compute the implicit temporal relationships inferred by a set of asserted linear inequalities, i.e. temporal constraint propagation [5]. For example, from the assertions “Given that Dick leaves for work within 10 minutes of 8:00 AM and his commute takes between 30 and 45 minutes, and Jane arrives at work within 15 minutes of 9:00 AM, is it possible for Jane to arrive at work before Dick? What is the latest after Dick that Jane could arrive?” Such tasks were useful for AI planning applications. The second task entailed solving a set of linear temporal inequalities, i.e., computing the set of time points that collectively satisfy all of the constraints represented by the inequalities [2]. This task, often characterized as the Temporal Constraint Satisfaction Problem (TCSP), addressed a variety of automated planning and scheduling problems.

However, fewer researchers addressed methods to match temporal relationships formally expressed as combinations of linear inequalities to time-stamped or temporally-annotated data. This “temporal pattern matching” (TPM) task aims to identify all existing data instances that satisfy a set of temporal constraints or to evaluate whether a specific data instance satisfies such a set. Many applications of TMP exist in the health care domain.

TMP is an important task in identifying cohorts of patients in clinical data repositories that satisfy the eligibility criteria for randomized trials or observational research studies, which can often be complex [6, 7,8]. For example, a study may only include patients who experienced a certain condition within one week after being administered a suspected medication, while excluding patients who were taking more than two other medications at the time the condition occurred or who had previously experienced the condition in the six months prior to being administered the suspected medication. TMP is also important in correctly applying automated clinical decision support rules to patient data, including clinical practice guidelines and alerts, when the logic of such rules specifies a particular sequence of two events or a specific temporal proximity of two events [9]. For example, an alert rule may be programmed to suggest the administration of a COVID vaccine only for patients with no positive COVID test during the 90 days prior to their visit. The specifications for electronic clinical quality measures also include temporal inclusion and exclusion criteria for correctly computing whether health care providers performed tests or interventions associated with high-quality care [10]. Beyond these data-analytical needs, the logical definitions of certain medical concepts in clinical terminologies, such as SNOMED-CT, also include temporal qualifiers. For example, a “post-surgical infection” is formally defined as the concept “infection” occurring after the concept “surgery”. The correct automated classification of such concepts requires deducing whether their temporal constraints subsume each other, i.e., whether one constraint “matches” the temporal pattern of another because it logically implies it [11]. For example, the concept “infection 1-7 days after surgery” is subsumed by and should be classified below the concept “infection after surgery” because the temporal pattern of the former necessarily implies that of the latter.

Previous researchers in medical informatics have explored the computable representation of abstract temporal relationships between events (i.e., temporal patterns) and the use of such representations in the evaluation or retrieval of patient data. Kohane’s model for temporal reasoning in expert systems defined the logical predicate “Range Relation” (RREL) to represent temporal relationships between medical events and/or states [12]. Although modeled as logical predicates, Range Relations essentially represented linear inequalities between the beginning and/or ending points of time intervals. The syntax of Range Relations allowed the representation of various metric relationships between such intervals, and an inference engine performed pattern matching between Range Relations and stored patient data to retrieve temporally matching instances. The model, however, did not formalize the semantics of Range Relations or the inference operations upon them. Hence, the semantics and computational complexity of such pattern matching remained uncertain.

Later, Das [13,14] defined a formal model to standardize the representation and querying of data stored in time-stamped relational databases, with semantics grounded in the set theory of the relational model. Das’s representation of temporal patterns was limited by not explicitly supporting ranges and metric constraints, such as “within two hours before or four hours after”, and by only retrieving data from relational databases. Subsequent to Das’s work, Shahar defined a general-purpose framework for knowledge-based temporal abstraction, which included a model for representing temporal relationships between intervals and an inference mechanism to retrieve patient data that matched specified patterns [15,16] Shahar’s representation of temporal patterns, like Kohane’s, consisted of linear inequalities over the starting and/or ending points of intervals. But like Kohane, Shahar also did not formalize the semantics of these representations, nor describe the algorithm(s) he implemented to match patient data against such patterns. In the absence of such details, the range of semantics that Shahar’s temporal-matching model could express and the computational complexity of its inferences also remained uncertain. A number of later researchers adopted Shahar’s temporal pattern-matching framework to develop derivative temporal reasoning systems for a variety of specific tasks [17,18], but they, too, did not further formalize or characterize the pattern-matching model. Further, their pattern-matching algorithms were often implemented in opaque software modules that were custom coded for each temporal pattern that needed to be specified [18], which complicated the programming and maintenance of these systems.

Other researchers explored the use of linear inequalities to annotate, in a computable form, the temporal relationships appearing in narrative, unstructured medical documents (such as discharge summaries) [19] and to computably annotate temporal relationships specified in clinical research eligibility criteria [6]. These efforts were valuable in demonstrating that many colloquial concepts of time that appear in narrative data and eligibility criteria can be represented mathematically as linear inequalities, but they did not precisely formalize the semantics of these representations, nor characterize the algorithms needed to correctly match them to each other.

To summarize, the disadvantages of these prior temporal models in the medical domain are that they did not formalize their semantics for representing temporal relationships between pair of events, they did not generalize their temporal pattern-matching algorithms to a single implementation that could handle any represented patterns, and they did not formally prove the soundness or explore the computational complexity of their temporal pattern-matching algorithms.

In this paper, we aim to fill these gaps by formally defining and proving the soundness of (1) a model based on linear inequalities for representing a variety of temporal relationships between pairs of intervals, and (2) an efficient and general-purpose algorithm to deduce whether one temporal relationship represented using this model satisfies (i.e., matches the pattern of, is subsumed by) another temporal relationship.

The described model and algorithm are applicable to a variety of automated temporal pattern-matching and temporal subsumption-testing tasks, including the examples below:

1. Enabling a decision-support system to correctly determine that a specific patient matches the antecedent of the decision-support rule “If infection occurs within two weeks of surgery, …” based on the following structured observation in the patient’s medical record: “The skin infection on the lower abdomen began 10 days after the patient underwent an appendectomy, and resolved two weeks later.”

2. Enabling a data-query application to find all patients at a hospital who were started on mechanical ventilation at some point during an inpatient surgery and remained on ventilation continuously for at least 18 hours after the conclusion of surgery, assuming that the hospital’s database records the start and stop times of all surgical procedures and the start and stop times of all treatments with mechanical ventilation.

3. Enabling medical terminology and ontology systems based on description logic (such as SNOMED-CT [20]) to correctly classify concepts such as the following with respect to each other: “Atrial Fibrillation occurring within 24 hours of surgery”, “Arrhythmia occurring during surgery or within two days after surgery”, “Atrial Fibrillation occurring after surgery”, “Asystole occurring during thoracic surgery”, and “Heart abnormality occurring during surgery or within 1 day after surgery”.

2.1 Examples

Before formally defining the model and algorithm, we present several examples of its use in practice so as to introduce the reader to its syntax and application. In general, the model requires the encoding of temporal relationships between pairs of events so as to represent the semantics of the relationships in a structured, logic-based manner. These encodings then support automated subsumption testing, i.e., the logical deduction of whether one relationship necessarily satisfies (i.e., is subsumed by) another relationship. The examples below are a brief introduction to the model, which is fully explained and formally defined in the sections that follow.

Note that each of the examples entails the representation of temporal relationships between two events, Event_X and Event_Y. Each of the events is assumed to occur over a temporal interval, I_X and I_Y, and each of these intervals is assumed to be defined by a pair of beginning and ending timestamps, b_X, e_X and b_Y, e_Y, respectively. For example, denotes that Event_X occurs within 14 days after Event_Y (again, the details of the notation are explained in the sections that follow). Each expression between the curly braces in the encodings represents an allowed duration between a pair of timestamps, with the first letter of the expression prefix corresponding to the beginning or ending timestamp of the interval for Event_X and the second letter corresponding of the beginning or ending time stamp of the temporal interval for Event_Y. For example, the expression above denotes that the beginning timestamp of Event_X (i.e., b_X) must be between 0 days and 14 days after the ending timestamp of the Event_Y (i.e., e_Y). In other words, it encodes the temporal constraint: 0 days < b_X – e_Y <= 14 days. Similarly, the expression denotes that the ending timestamp of Event_X (i.e., e_X) occurs on the 17^th day after the ending timestamp of Event_Y (i.e., e_Y). In other words, it encodes the temporal constraint: 16 days < e_X – e_Y <= 17 days (or, more colloquially, the temporal relationship “ends 17 days after”).

2.2 Preliminary Assumptions and Definitions

We define a temporal concept as a class of events/conditions/states/etc., and an event as an instance of a temporal concept. For example, the concept Open-Heart Surgery is a temporal concept, and a specific open-heart surgery procedure performed on a specific patient at a specific time is an event. Note that, in the medical domain, events may be symptoms, diseases, procedures, clinical states, or any other phenomena that exist over a defined period of time (i.e., not necessarily “events,” per se). For example, the abdominal pain that the patient Mary L. Smith experienced between 7:00 PM on January 21^st, 2023 and 8:00 AM on January 22^nd, 2023 is an event that is an instance of the temporal concept Abdominal-Pain.

Each event exists during a finite interval of time, I (its event interval). Each event interval I_X is defined by a beginning timestamp b_X and an ending timestamp e_X, where b_X and e_X are discrete time points on a single fully-ordered linear timeline and -∞ < b_X ≤ e_X < +∞. In the model defined here, these timestamps are specified at a granularity of one second, although variations of the model could specify timestamps at smaller temporal granularities (e.g., one microsecond). The functions b() and e() exist over all temporal intervals I and return the beginning and ending timestamps of the intervals, such that b(I_X) = b_X and e(I_X) = e_X. The duration of any interval I_X is equal to e(I_X) - b(I_X) (or, alternatively, e_X – b_X). Note that “instantaneous” events may exist such that b(I_X) = e(I_X), i.e., the duration of the event = 0.

A relative temporal duration is the duration of time between two timestamps, t₁ and t₂, which could pertain to two different intervals. This duration may be expressed using any unit of measure greater or equal to the minimum time-point granularity. For example, the following expression denotes the relative temporal duration between the ending timestamp of the temporal interval I_X and the beginning timestamp of the temporal interval I_Y: e(I_X) – b(I_Y) = -12 hours (“I_X ended exactly 12 hours before I_Y began”). Note that relative temporal durations may be positive or negative.

When the minimum time-point granularity is one second, as specified in our model, the allowed units of measure for relative temporal durations are seconds, minutes, hours, days, weeks, months, and years.

Note that the actual beginning and ending timestamps of events need not be known for the model to express temporal relationships between temporal concepts and for the algorithm to make inferences regarding such relationships, specifically subsumption testing. The conceptual existence of temporal intervals with beginning/ending timestamps simply form the formal basis on which the representational model and inference algorithm, including their formal semantics, are based.

2.3 Relative Temporal Interval Predicates

A Relative Temporal Interval Predicate (RTIP) is a formal predicate expression that denotes a constraint on the relative temporal duration between a pair of beginning and ending timestamps belonging to two different temporal intervals. For example, an RTIP might specify that the ending timestamp of the temporal interval corresponding to Event_X must precede the beginning timestamp of the temporal interval corresponding to Event_Y by a duration greater than 0 days, thereby expressing the constraint “Event_X ends before Event_Y begins.” We define the syntax and semantics of RTIPs in the following two sections.

2.4 RTIP Syntax

RTIP ::= (“BB” | “BE” | “EB” | “EE”) LOWER-BOUND “,” UPPER-BOUND

LOWER-BOUND ::= (FINITE-LOWER-BOUND | INFINITE-LOWER-BOUND)

UPPER-BOUND ::= (FINITE-UPPER-BOUND | INFINITE-UPPER-BOUND)

FINITE-LOWER-BOUND ::= (“[“| “(“) REAL-NUMBER UNIT-OF-MEASURE

INFINITE-LOWER-BOUND ::= “(-INF”

FINITE-UPPER-BOUND ::= REAL-NUMBER UNIT-OF-MEASURE (“)” | “]”)

INFINITE-UPPER-BOUND ::= “+INF)”

REAL-NUMBER ::= Any real number

UNIT-OF-MEASURE ::= (“sc” | “mn” | “hr” | “dy” | “wk” | “mo” | “yr”)

Below are examples of several RTIP expressions and their informal meanings. The formal semantics of RTIP expressions, in general, are presented in the following section.

BB[0dy,+INF) (Event_X begins any time after Event_Y begins)

BE[1wk,3.5wk] (Event_X begins between 1 week and 3.5 weeks after Event_Y ends)

EB(-INF,0dy) (Event_X ends any time before Event_Y begins)

EE[-1dy,1dy] (Event_X ends between 1 day before and 1 day after Event_Y ends)

Note that implicit in the syntactic expression of each RTIP is the pair of temporal intervals over which the predicate is defined, I_X and I_Y. For example, the RTIP “BB[0dy,+INF)” actually expresses the predicate “BB[0dy,+INF)[I_X,I_Y]”, such that, for any pair of temporal intervals I_X and I_Y, the RTIP evaluates to either logical TRUE or FALSE.

2.5 RTIP Semantics

As mentioned, RTIPs express a constraint on the duration between the beginning or ending timestamps of one temporal interval I_X and the beginning or ending timestamps of another temporal interval I_Y. The two capitalized letters at the beginning of each RTIP express the pair of timestamps to which the RTIP constraint applies. For any two intervals, there are four combinations of such timestamps, and hence four types of RTIPs may be signified by the two capitalized letters. The semantics of the four types are defined as follows:

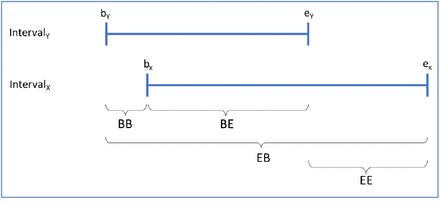
Figure 1 illustrates the relative temporal durations constrained by each type of RTIP, using two example intervals (recall that relative temporal durations may be negative).

• Download figure
• Open in new tab

Figure 1. Graphical representation of the four types of RTIPs.

Each RTIP constrains the relative temporal duration between two timestamps to a range of values, and the bounds of this range may assume any finite values between -∞ and +∞ (as well as infinite values, as described below). Finite values of relative temporal duration may be expressed using any of the following temporal units of measure (with their corresponding syntactic tokens): Seconds (“sc”), minutes (“mn”), hours (“hr”), days (“dy”), weeks (“wk”), months (“mn”), and years (“yr”). The model described here establishes the following fixed and consistent conversion factors among these units of measure: The range specified in each RTIP is defined by a lower and an upper bound, which may each be open or closed. The prefixes “[“and “(“within the lower bound and the suffixes “)” and “]” within the upper bound denote whether the lower and upper bounds of a range are open or closed. Per convention, open bounds are denoted with the characters “(“and “)” and closed bounds with the characters “[“and “]”. The role of these characters in defining the full semantics of RTIPs is illustrated in the following examples (note that the semantics of the special values “(-INF” and “+INF)” will be defined in the following section).

More formally, the range specified by RTIPs of each type has a lower bound L and an upper bound U, such that we can rewrite an RTIP as ts₁ts₂ ^{L, U} where ts₁, ts₂ ∈ {B,E} and L,U are valid lower and upper bound expressions, such as “[1wk”, “(-INF”, “1dy]”, “+INF)”, etc. Per this alternative notation, for example, the following RTIP expressions are equivalent: “BB[5dy,+INF)” and “BB^{≥ 5dy,< +INF}”. We also define f_ts as one of the functions “b()” or “e()” that return the beginning or ending timestamp of a temporal interval, respectively (as defined in Section 2.2) (i.e., f_B = b() and f_E = e()). We also define the function value() to return the value of a lower or upper bound expression, such that, for example, value(“[1wk”) = 1 week and value(“+INF)”) = +∞. In addition, we define the comparison operator “<*” as either one of the mathematical operators “<“or “≤”, depending on whether the corresponding lower or upper bound is open or closed. Lastly, we recall that implicit in the syntactic expression of each RTIP is the pair of temporal intervals, I_X and I_Y, over which the predicate is defined.

Using this notation, the formal semantics of an RTIP are defined as follows: Hence, the formal semantics of are Table 1 contains several examples showing how this general definition indicates the semantics of other specific RTIP expressions.

To later assist in defining subsumption over RTIPs, we also define the predicate Satisfies-Bound() to denote that a particular relative temporal duration (rtd), such as e(I_X) - b(I_Y), satisfies the constraint imposed by a particular lower or upper bound (L or U) in an RTIP. For example, if an rtd = 3 days and L = “[1dy”, then Satisfies-Bound(rtd, L) = TRUE because 1 day ≤ 3 days. Conversely, if U = “-2dy)”, then Satisfies-Bound(rtd, U) = FALSE because 3 days ≮-2 days. Using these predicates, we can restate the semantics of an RTIP as follows: In other words, an RTIP evaluates to TRUE if and only if the indicated relative temporal duration between two intervals satisfies both the lower-bound constraint and the upper-bound constraint of the RTIP. For example,

2.6 Relative Temporal Relationships

Not all useful temporal relationships between pairs of events can be expressed as a single RTIP. For example, expressing the familiar concept of “during” requires the logical conjunction of two RTIPs: BB[0dy,+INF) AND EE(-INF,0dy] (i.e., I_X begins at or after the beginning of I_Y and ends at or before the ending of I_Y). As such, we define more generally a Relative Temporal Relationship (RTR) between two temporal intervals I_X and I_Y as a logical formula consisting of the conjunction of one or more RTIPs, each defined over the same pair of temporal intervals. We will later generalize this definition to also allow disjunctions of RTIPs within the logical formulae that specify an RTR, but we initially define and prove a model that allows conjunctions only.

2.7 RTR Syntax

The syntax of RTRs is defined as follows (with the syntax of “RTIP” remaining as specified above). RTR ::= RTIP (“&” RTIP)*

Example RTR expressions: Again, note that implicit in the syntactic expression of each constituent RTIP is the pair of temporal intervals over which the predicate is defined, I_X and I_Y. For example, the RTR actually expresses the conjoined predicates such that, for the single pair of temporal intervals I_X and I_Y, the conjunction evaluates to either logical TRUE or FALSE.

Given that all of the RTIPs that specify an RTR are defined over the same pair of temporal intervals, I_X and I_Y, it is implicit that the RTR specified by a conjunction of RTIPs is defined over the same pair of intervals, i.e. RTR[I_X,I_Y]. RTRs are, therefore, themselves predicates that can evaluate to TRUE or FALSE.

2.8 RTR Semantics

As noted, an RTR is, itself, a logical predicate defined over a pair of temporal intervals I_X and I_Y. The semantics of this predicate are defined as the logical conjunction of the RTR’s constituent RTIPs: In other words, two temporal intervals satisfy the constraints of an RTR if and only if they satisfy the constraints of all the RTIPs conjoined within the RTR. As a corollary, an RTR can represent any temporal relationship that can be expressed as the conjunction of one or more RTIPs. Although this expressiveness admits a large range of familiar and less-familiar temporal relationships, including “before”, “after”, “during”, “during and after”, and “within 5 hours after,” it cannot express certain other temporal relationships, such as “before or after”. The addition of disjunction to RTR expressions in Section 2.10 will address this limitation, but for the time being we will introduce and formalize the notion of subsumption between RTRs that are limited to conjunctions only. Extending the model to include disjunctions will then follow in a straightforward manner.

2.9 Subsumption Between Relative Temporal Relationships

We have thus far defined an RTR as the conjunction of one or more RTIPs, each of which defines a constraint between two temporal intervals, I_X and I_Y. We have further defined the semantics of an RTR as the semantics of the logical formula expressed by this conjunction. In other words, two temporal intervals, I_X and I_Y, satisfy an RTR if they satisfy all of the conjoined predicates that comprise the RTR. For example, two temporal intervals I_X and I_Y satisfy the RTR that denotes “during” (i.e., interval I_X occurs during the interval I_Y) if they satisfy both the RTIPs “BB[0dy,+INF)” and “EE(-INF,0dy].”

We now define the notion of subsumption between two RTRs as follows: RTR_i is subsumed by RTR_j (and RTR_j subsumes by RTR_i) if and only if every pair of intervals I_X and I_Y that satisfies the logical formula RTR_i necessarily also satisfies RTR_j. We can denote this relationship as RTR_i ⊑ RTR_j. As an example, we intuitively know that the temporal relationship “during” is subsumed by the temporal relationship “during or after” because any interval I_X that occurs during any interval I_Y also necessarily occurs during or after the interval I_Y. Conversely, we intuitively know that the temporal relationship “before or during” does not subsume the temporal relationship “during or after,” because it is possible that an interval I_X that occurs before or during an interval I_Y does not occur during or after I_Y (specifically, if I_X occurs before I_Y). Note that, in the latter example, an interval I_X that satisfies “before or during” with respect to I_Y may also satisfy “during or after,” but it does not necessarily do so (unlike in the former example, in which satisfaction of “during” by any pair of intervals necessarily implies satisfaction of “during or after”).

The purpose of our work has been to develop a formal symbolic representation model for temporal relationships and an automated inference algorithm that correctly calculates whether any one such temporal relationship subsumes another. As discussed in the introduction, determining whether one temporal relationship between two intervals (or, equivalently, between two events) subsumes another is practically useful for performing temporal pattern matching in the application of decision-support logic or in the analysis of clinical data, as well as for classifying temporally-qualified concepts in biomedical ontologies. Below, we present and prove a logically sound algorithm to test subsumption between any two temporal relationship that are expressed as RTRs (i.e., using the syntax and semantics defined above).

2.10 Representing and Reasoning with Temporal Relationships That Include Disjunctions

We have thus far defined a sound algorithm for testing subsumption between temporal relationships that can be represented as a conjunction of RTIPs. We now generalize this algorithm to test subsumption between temporal relationships that can be represented as any combination of conjunctions and disjunctions of RTIPs. This generalization is necessary to accommodate common temporal relationships such as “before or after”, as well as more complex relationships, such as “During the first trimester or the third trimester” and “Present at the beginning or the end of”.

We first generalize the syntax of RTRs by adding the disjunction operator, as well as parentheses symbols to designate the intended precedence when conjunctions and disjunctions are combined. The syntax for generalized RTRs (“GRTRs”) is therefore:

GRTR ::= CONJUNCTION-OR-DISJUNCTION ([“&” | “|”] CONJUNCTION-OR-DISJUNCTION)*

CONJUNCTION-OR-DISJUNCTION ::= CONJUNCTION | DISJUNCTION

CONJUNCTION ::= “(“RTIP (“&” RTIP)* “)”

DISJUNCTION ::= “(“RTIP (“|” RTIP)* “)”

Examples of valid GRTR expressions (and their intended meanings): The semantics of RTRs are likewise generalized to reflect that they may now be combinations of disjunctions and conjunctions of RTIPs. To formalize the semantics of such generalized RTRs (GRTRs), first we note that any logical formula consisting of conjunctions and disjunctions of predicates can be converted to a logically equivalent Normal Disjunctive Form (NDF), i.e., a disjunction of conjoined predicates [22]. When all such predicates are RTIPs over pair of the temporal intervals I_X and I_Y, we can rewrite any GRTR that has been converted to an NDF as: The semantics of a GRTR are, therefore, defined as the NDF of the combination of disjunctions and conjunctions of RTIPs that specifies the GRTR: Finally, we generalize the definition of subsumption between any pair of GRTRs as follows: GRTR_a is subsumed by GRTR_b (and GRTR_b subsumes GRTR_a) if and only if every pair of intervals I_X and I_Y that satisfies the logical formula GRTR_a necessarily also satisfies GRTR_b. If we again use the symbol ⊑ to denote subsumption, then we define Given the semantics of GRTRs as defined above, we can restate the semantics of subsumption between any pair of GRTRs, GRTR_a and GRTR_b as follows: Hence, to test subsumption between GRTRs, we update the subsumption-testing algorithm specified above as follows.

As a first step, convert each GRTR to its Normal Disjunctive Form. Following this conversion, each GRTR will be of the form Note that each conjunction in this expression, (⋂_j=1..mRTIP_j)_i, is itself an RTR as defined above (i.e., a conjunction of RTIPs). We can therefore rewrite each GRTR as And we can rewrite the definition of subsumption between two GRTRs as GRTR_a ⊑ GRTR_b ≡ In other words, GRTR_a ⊑ GRTR_b if and only if the disjunction of RTRs that define GRTR_a implies the disjunction of RTRs that implies GRTR_b. To test whether the implication in the definition above is true, the subsumption algorithm determines (using the subsumption-testing algorithm for RTRs as defined and proven above, including the normalization steps) whether every RTR within the disjunction on the lefthand side of the implication is subsumed by at least one RTR on the righthand side of the implication. In other words, the subsumption algorithm evaluates the truth of the following predicate logic expression: GRTR_a ⊑ GRTR_b if and only if this logical sentence is TRUE given the definitions of each RTR.

Claim 7: For any two GTRTs, GRTR_a and GRTR_b, where Proof: The proof for Claim 7 is provided in the Appendix, Section 7.6

2.11 Computational Complexity of the Subsumption-Testing Algorithm

We assert that the computational complexity of testing subsumption between any pair of GRTRs, as described above, is proportional only to the number of disjoined RTRs that appear in the specifications of the two GRTRs. In particular, the number of operations required to test subsumption between two GRTRs in the course of classifying a concept within a terminology/ontology does not at all depend on the size or complexity of the terminology/ontology. Likewise, the number of operations required to test subsumption between two GRTRs in the course of querying an EHR does not at all depend on the number of records in the EHR. Subsumption testing between two GRTRs is a deterministic and “localized” operation, and the number of steps required to perform it depends only on the specification of the two GRTRs, themselves.

Specifically, the number of operations required to perform subsumption testing between two GRTRs is proportional to either (1) the product of the number of disjoined RTRs used to specify the candidate and the reference relationships being tested, or (2) the sum of the number of disjoined RTRs used to specify the candidate and the reference relationships being tested, whichever is larger.

For example, given the following specifications for two GRTRs: the product of the number of RTRs is 3 x 2 = 6, and the sum of the number of RTRs is 3 + 2 = 5. Hence, the performance of the algorithm to test the proposition GRTR_a ⊑ GRTR_b is O(6).

In general, if the number of conjoined RTRs in GRTR_a is n, and the number of conjoined RTRs in GRTR_b is m, then the performance of the operation to test whether GRTR_a ⊑ GRTR_b is O(max(n*m, n+m)). In the special case that GRTR_a and GRTR_b each consist of only a single RTR, the performance of the subsumption-testing operation is O(2).

Proof: As asserted in Claim 7, In the worst case, therefore, each RTR_i in the specification of the candidate GRTR will need to be subsumption tested against each RTR_k in the specification of the reference GRTR to determine whether the quantified logical sentence is true, resulting in no more than n * m subsumption tests of the proposition RTR_i ⊑ RTR_k. Because all RTRs in the specification of both the candidate and the predicate GRTR have been normalized, we know that each test of the proposition RTR_i ⊑ RTR_k requires exactly four tests of subsumption with respect to the corresponding (same-type) RTIPs in each RTR, i.e., specifically the subsumption tests: Each such subsumption test of RTIPs is a constant-time operation, as it requires only the comparison of the respective upper and lower bounds of the corresponding candidate and the reference RTIPs, per the algorithms to evaluate ⊑_L and ⊑_U, as specified in Section 2.9.1. Hence, the computational effort of testing whether GRTR_a ⊑ GRTR_b is proportional to n * m.

In the special cases where (n + m) > (n * m), the computational effort to normalize all of the RTRs in the predicate and candidate GRTRs may be greater than that of testing subsumption between the RTRs in the predicate GRTR and those in the candidate GRTRs. This is because each RTR in the predicate and candidate GRTRs needs to be normalized, and the normalization of each RTR is constant-time in the number of RTIPs that comprise the RTR, which should typically not exceed four (i.e., at most one for each type of RTIP – BB, BE, EB, an EE – as there is no additional information provided in specifying two RTIPs of the same type for an RTR). In the worst case, then, each RTR will consist of four RTIPs, which will each generate (during the expansion step of normalization) three additional RTIPs that are conjoined with those original RTIPs. At most, then, the expansion step will result in a total of 16 RTIPs for each RTR, with a maximum of four RTIPs of each type. Subsequently, up to three merge operations will be needed for each type of RTIP to reduce the four RTIPs to one RTIP during the consolidation step of normalization. Hence, normalizing each RTR will require no more than a total of: Hence, when (n + m) > (n * m), the total computational effort to test subsumption between two GRTRs may be dominated by the effort required to normalize all of the RTRs within the GRTRs. Note, however, that this situation will only arise when both n and m ≤ 2. However, these cases may be common, so the overall complexity of the subsumption-testing algorithm must be characterized as O(max(n*m, n+m)). In almost all cases, however, both n and m will be < 10, resulting in very efficient performance for the subsumption testing algorithm.

Note, in particular, that the computational complexity of classifying concepts within terminologies/ontologies that use the EL++ description logic (such as SNOMED-CT) is O(n^x) (i.e., polynomial). Hence, the additional computational effort required to augment the classification process with temporal subsumption (a constant-time operation) will be dominated by the polynomial-time operations already inherent in classification, and therefore will impact the overall performance of EL++ classifiers negligibly.