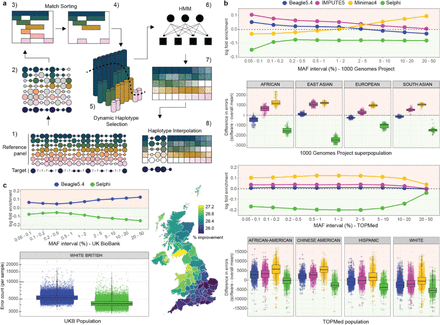
Abstract
Genotype imputation, crucial in genomics research, often faces accuracy limitations, notably for rarer variants. Leveraging data from the 1000 Genomes Project, TOPMed and UK Biobank, we demonstrate that Selphi, our novel imputation method, significantly outperforms Beagle5.4, Minimac4 and IMPUTE5 across various metrics (12.5%-26.5% as measured by error count) and allele frequencies (13.0%-27.1% for low-frequency variants).This improvement in accuracy boosts variant discovery in GWAS and improves polygenic risk scores.
Main
Genomic medicine promises to deepen our knowledge of disease pathology, improve diagnostic speed and accuracy, and enable targeted disease treatment and preventive therapy1. However, as high coverage whole genome sequencing (hc-WGS) is still prohibitively expensive, especially when it comes to large scale population-wide screening, a lot of academic and direct-to-consumer efforts rely on array-based SNP genotyping and low-coverage WGS (lcWGS). These approaches are cost-effective, but their accuracy depends on imputation, which has a profound impact on all downstream applications of these datasets, such as detecting associated variants in genome-wide association studies (GWAS) or calculating polygenic risk scores (PRS)2,3.
Over the last twenty years, multiple groups have developed different state-of-the-art imputation methods4,5,6. However, these models still suffer in accuracy when imputing rare variants7,8. This is of note because rare variants can be highly informative and of great medical significance9. Recently, efforts have been made to address this by creating cohort-specific reference panels10,11,12 or adding whole exome sequencing data to the panel13. The improvement of rare variant imputation by addressing the algorithm itself hasn’t been convincingly demonstrated yet. Here, we describe a new imputation tool that does this by identifying and giving priority to potential identity by descent (IBD) segments.
Selphi is a haploid imputation model developed in python and C that builds on the Li and Stephens HMM model14. In our implementation, the algorithm identifies matches to reference haplotypes using a version of the Positional Burrow Wheeler Transform (PBWT)15, adept at identifying the longest haplotype matches between the target and reference sequences.
Additionally Selphi performs an IBD selection heuristic at each genotyped marker to eliminate possible identity by state (IBS) matches. This heuristic reduces false positives arising from coincidental identical genotypes between individuals, not attributed to genetic lineage but chance (Fig. 1a; see Methods for more details).
(a) The first step in the workflow merges the reference panel and target data into a unified PBWT data structure (1). The algorithm then scans the reference panel searching for matches to reference haplotypes of a minimum length (2). At each marker, the algorithm retains the longest matches, prioritizing haplotypes with more total matches across the chromosome (3-4). Dynamic haplotype selection follows, where the matches are mapped and filtered to adjust the number of retained matches at each marker, based on the distribution of match lengths (5). An HMM forward-backward algorithm is employed (6). Transitions between variant states are utilized to compute weights for each haplotype at each marker. The weights aid in determining the significance of each haplotype within the population (7). The final step interpolates allele probabilities with the haplotypes from the reference panel (8). (b) Relative enrichment (red background) and depletion (green background) of error counts with respect to average for Beagle5.4 (blue), IMPUTE5 (magenta), Minimac4 (yellow) and Selphi (green) across chromosomes 1-22 of the 1000 Genomes Project (1KG) and for chromosome 20 of the TOPMed dataset. (c) Relative enrichment and depletion of error counts with respect to average and error count per sample for chromosomes 1-22 of the UK Biobank dataset. Map shows improvement in imputation accuracy across UK counties against Beagle5.4.
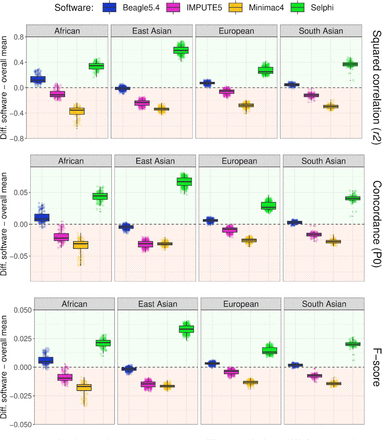
To benchmark Selphi’s performance, we first compared it against Beagle5.44, IMPUTE55 and Minimac46, using chromosomes 1-22 of the 1000 Genomes Project (1KG)16. 1KG has been widely used as a gold-standard dataset for testing imputation accuracy4,7,8. Selphi had the lowest number of errors across all minor allele frequency (MAF) intervals and ancestral backgrounds (Fig. 1b). It performed exceedingly well for rare (MAF 0.05-2%) and particularly for ultra-rare (MAF 0.05-0.1%) variants, with an average improvement of 13% and 21%, respectively. The improvement was particularly pronounced in the East Asian and African super-populations. We additionally assessed the accuracy of each method using squared correlation (r2), concordance (P0) and F-score. Selphi remained the best method across all evaluated metrics across all ancestries (Extended Data Fig. 1, Supplementary tables 1-2).
Difference in squared correlation, concordance, and F-score between Beagle5.4 (blue), IMPUTE5 (magenta), Minimac4 (yellow), and Selphi (green) for chromosomes 1-22 across different super-populations. The difference is shown as the deviation from the average number of errors across all four methods.
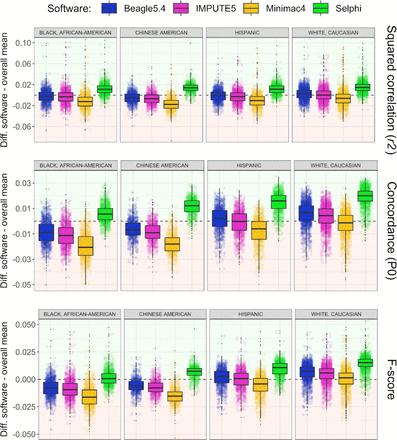
Next, we benchmarked Selphi using chromosome 20 of TOPMed17, a large, ethnically and ancestrally diverse dataset that is increasingly used to improve imputation accuracy, especially in admixed populations18. 5,000 samples from the TOPMed dataset’s Multi-Ethnic Study of Atherosclerosis (MESA) were imputed against the remaining 85,897 hc-WGS TOPMed samples as the reference panel. Selphi, again, achieved the best results with the lowest number of errors, with an average improvement of 27.1% for rare variants (MAF 0.05-2%) (Fig. 1b; Extended Data Fig. 2; Supplementary tables 1,3).
Difference in squared correlation, concordance, and F-score between Beagle5.4 (blue), IMPUTE5 (magenta), Minimac4 (yellow), and Selphi (green) for chromosome 20 across different super-populations. The difference is shown as the deviation from the average number of errors across all four methods.
In addition, to demonstrate its applicability to larger datasets, we benchmarked Selphi against Beagle5.4, the next most accurate model in our analysis, using the UK Biobank dataset19. We imputed chromosomes 1-22 of 50,000 samples classified as white British. Selphi performed better than Beagle5.4 for all MAFs (Fig. 1c). On average, Selphi accomplished a ∼25% increase in concordance over Beagle5.4, with an improvement of 13.4% for rare variants (MAF 0.05-2%). Also notably, for the MAF interval of 20-50%, Selphi made around 20,000 fewer errors per sample, achieving 33.4% improvement (Supplementary tables 1,4).
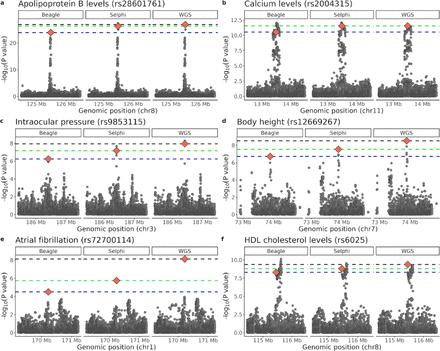
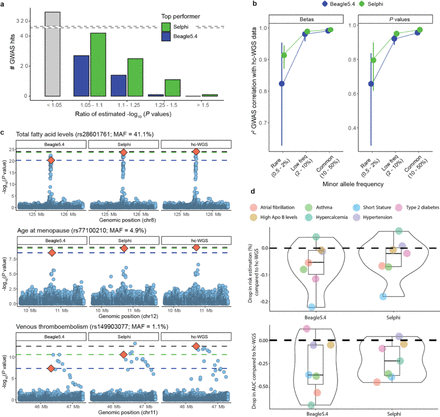
To ascertain that improved imputation accuracy would boost GWAS variant discovery, we used 50,000 unrelated White British samples from the UK Biobank that possessed both genotyping and hc-WGS information, and imputed their genotyping data using Selphi and Beagle5.4. Next, we conducted GWAS for 50 distinct traits using the imputed datasets. Selphi yielded results in closer alignment with the hc-WGS data, especially for rare variants (Fig. 2a-c, Extended Data Fig. 3). Finally, we used the GWAS results to create polygenic risk scores (PRS) for seven different phenotypes. Imputation by Selphi produced PRSs in closer alignment to that of hc-WGS (Fig. 2d).
Red diamond indicates the known GWAS signal collected by the GWAS Catalog and the horizontal lines, the significance achieved by Beagle5.4 (blue), Selphi (green) and hc-WGS (black) for these.
(a) Number of GWAS hits in which Selphi or Beagle obtained higher significance, plotted by ratio bin. Variants that surpassed GWAS suggestive threshold (P < 10-5) were analyzed. A ratio below 1.05 was considered as an equivalent result for both Beagle and Selphi. (b) Squared correlation (r2) for betas and P values obtained from imputed sets and compared to hc-WGS across 50 UK biobank phenotypes by MAF. Nominally significant (P < 0.05) trait-associated hits collected by the GWAS Catalog were retrieved. Lower and upper limits of the forest plot represent the confidence interval from bootstrap resampling. (c) GWAS examples of imputed sets along with hc-WGS results. Red diamond indicates known GWAS signals. (d) PRS drop in accuracy when comparing imputed sets with hc-WGS, assessed through relative risk and area under the curve (AUC).
Genotype imputation will likely continue to be an important part of genomic studies, especially as large population-wide genotyping efforts expand. Selphi can enable researchers to impute and re-impute a larger number of rare variants to a higher quality. One of the main challenges in imputing rare variants is the lack of a suitable or large enough reference panel. Unlike recent efforts to broaden and manipulate the reference panel10,11,12,13, Selphi increases accuracy within existing panels. This is of particular importance when there is not enough data to expand the panels, which is often the case in non-European populations. Notably, Selphi achieved pronounced improvements in East Asian and African populations of the 1000 Genomes Project and Chinese Americans in the TOPMed dataset. This suggests considerable promise for increasing imputation accuracy in populations that have been historically underrepresented in genetic research20. We also demonstrate that Selphi can improve GWAS variant discovery and PRS calculation without manipulating the reference panel, obtaining results in closer alignment to hc-WGS. This advance in imputation, therefore, has the potential to improve the accuracy and resolution of future genomic studies.
Funding
All work was funded by a commercial source, Omics Edge, a subsidiary of Genius Labs Company. Omics Edge provided only funding for the study, but had no additional role in study design, data collection and analysis, decision to publish or preparation of the manuscript beyond the funding of the contributors’ salaries.
Author contributions
Conceptualization: A.D.M. and P.G.Y. Data Curation: A.D.M., A.A.M., S.B., S.L. and A.T. Formal Analysis: A.D.M., A.A.M., S.B., J.L.J. and S.L. Software: A.D.M., A.A.M., S.B., C.M. and M.M. Methodology: A.D.M. and P.G.Y. Investigation: A.D.M., A.A.M., S.B., J.L.J., B.N. and C.M. Visualization: A.D.M., A.A.M., S.B., J.L.J. and B.N. Writing – original draft: A.D.M., A.A.M. and B.N. Writing – review & editing: A.D.M., S.B., J.L.J., B.N., S.L., A.T and P.G.Y. Funding acquisition: A.T and P.G.Y. Project administration: A.T and P.G.Y. Resources: A.T and P.G.Y. Supervision: A.T and P.G.Y.
Competing interests
A.D.M., A.A.M., S.B., J.L.J., B.N., C.M., A.T, M. M. and P. G. Y. are either employed by and/or hold stock or stock options in Omics Edge, a subsidiary of Genius Labs. In addition, P.G.Y. has equity in Systomic Health LLC and Ethobiotics LLC. This does not alter our adherence to journal policies on sharing data and materials. There are no other relevant activities or financial relationships which have influenced this work.
Data availability
The complete documented Selphi code is available for testing for academic/non commercial use in the following GitHub repository: https://github.com/selfdecode/rd-imputation-selphi. Additionally, we offer an applet that allows users to conveniently test the Selphi code on the UKB RAP platform.
All publicly available datasets utilized in this study can be accessed through their original publications and via application to the UK Biobank. Furthermore, access to The Trans-Omics for Precision Medicine (TOPMed) dataset can be granted by the National Institutes of Health (NIH).
Additional Information
Supplementary Information is available for this paper.
Correspondence and requests should be addressed to pyazdi{at}omicsedge.com.
Online Methods
Selphi
Model Overview
Selphi was developed in Python and C and uses vectorized matrix functionalities of numpy for efficient processing in large-scale data environments. It operates under the assumption that both reference and target genotypes are phased and non-missing. We categorize markers as “reference markers” (genotyped in the reference panel), “target markers” (genotyped in the target samples), and “imputed markers” (present in the reference panel but ungenotyped in the target samples).
The imputation process relies on the concept of identity by descent (IBD), identifying chromosome segments inherited from a common ancestor uninterrupted by recombination events. Utilizing genotypes at target markers, we accurately pinpoint IBD segments shared between target and reference samples, allowing for the transfer of un-genotyped alleles from reference to target haplotypes.
To address uncertainty in IBD inference, we use a modified probabilistic Li and Stephens Hidden Markov Model (HMM)14, which produces posterior probabilities for each potential allele at an imputed marker on the target haplotype. Selphi considers each haplotype within the reference panel as a discrete state in a HMM, with each genotype as a distinct observational entity. The model employs an optimized version of the forward-backward algorithm for vectorized operations to estimate the likelihood of hidden states at each imputed genetic marker.
This estimation involves calculating probabilities based on genotypic data from the target sample and haplotypes in the reference dataset.
PBWT
For improved precision, Selphi integrates the Positional Burrow Wheeler Transformation (PBWT)15, adept at identifying the longest haplotype matches between the target and reference sequences. The model also includes a heuristic Identity by Descent (IBD) selection at each genotyped marker, crucial for filtering out Identity by State (IBS) matches. This heuristic reduces false positives arising from coincidental identical genotypes between individuals, not attributed to genetic linkage but chance.
In our model, the PBWT assumes a crucial role as the foundational algorithm for streamlined genomic data analysis. PBWT encompasses a set of algorithms tailored for proficiently searching and compressing genetic data. Its primary objective is to arrange haplotypes in a reversed prefix order, a mechanism that markedly simplifies the identification and matching of haplotypes across reference panels.
The PBWT algorithm initiates with the construction of a positional prefix array. This array is essentially a sequence of haplotype indices, arranged such that the haplotypes are sorted in reverse prefix order at a given position, denoted as n. To achieve this, two distinct vectors, of length M, are created for each genotype marker at position n. One vector is responsible for holding the indices of haplotypes, sorted according to their reversed prefix order. The other vector tracks the index where the last match for each haplotype began, essentially marking the starting point of each haplotype match. This helps facilitate quick and memory-efficient pairwise comparisons between all haplotypes in the reference panel.
In the context of Selphi’s imputation process, the reference panel denoted as X with X ∈ {0,1}MxNand the target haplotype T with T ∈ {0,1}1xN are defined within a certain genomic structure. Here, N represents the total number of genotyped variants. The reference panel X and the target T are aligned such that they share a common set of markers, with the reference panel not necessarily containing a complete marker set but only those that overlap with the target.
The first crucial step in Selphi’s imputation process involves the computation of forward matches. This is achieved by accumulating previous matches for the same haplotype until a mismatch occurs, at which point the match count resets to zero. This mechanism is integral to the PBWT and is detailed in equation (1), describing the creation of BI data structures.
The algorithm then proceeds to compare each target haplotype against every reference haplotype at each variant. A match is recorded when there is a divergence, provided that the total length of the match exceeds a pre-set threshold, typically a minimum of five consecutive variants. This threshold ensures that only significant matches are considered, enhancing the accuracy of imputation. The matches are then organized into a sparse matrix format, which is particularly suited for handling data with a high proportion of zero values, common in genomic matrices. The sparse matrix, encapsulating the essential match data, is then saved as a .npz file for downstream use.
Haplotype selection
Haplotype selection begins with the creation of a custom match matrix, a structured representation where each entry correlates to the length of consecutive haplotype matches identified by PBWT. To refine this selection, Selphi constructs a filtering mask—a secondary matrix that delineates the maximum length of matches at each genomic marker. In this matrix, for each marker, the k haplotypes with the longest matches are retained, effectively filtering out less likely haplotypes and thus narrowing down the potential candidates for imputation.
With this filtered matrix, Selphi then assigns weights to each match, incorporating both the length of individual matches and the aggregated matching performance across all markers. These weighted values are stored in a weighted matrix (WH) and used in determining the haplotype’s contribution. Each haplotype is then weighted according to equation (2).
At each marker location within the genomic sequence, Selphi computes the standard deviation of match lengths across the spectrum of potential haplotypes. A length threshold is dynamically calculated for each marker. Haplotypes with match lengths falling short of this threshold are systematically excluded from consideration. The threshold itself is a function of both the calculated standard deviation and an adjustable scaling factor known as the knob parameter, which is subtracted from the maximum match value identified at each marker.
The knob parameter is calibrated against the mean and the longest possible match length normalized between 0.2 and 3 at each specific marker, providing a method to control the stringency of haplotype selection. A small knob value is applied when the average number of matches is high, warranting a stricter selection criterion due to the increased likelihood of encountering a true Identity by Descent (IBD) under these conditions. Conversely, a larger knob value is used when the average is low, relaxing the selection to account for variability and avoiding the exclusion of valid haplotypes. This strategic parameterization mitigates the undue influence of Identity by State (IBS) matches during the imputation process. So, the inclusion of the knob parameter allows for tunable specificity in haplotype selection, scaling the threshold in accordance with the average number of matches at a marker. Haplotype selection is conducted across the entire chromosome without segmenting it into windows. This is a distinguishing feature of our method, contrasting with others that divide the genome into smaller windows4,5. This comprehensive approach ensures the conservation of essential data derived from the pairing of target sequences with the reference panel. Moreover, it avoids the imputation inaccuracy near window boundaries, a known limitation in methods employing short, non-overlapping windows. Our technique, by processing the chromosomes as whole units, circumvents the potential loss of continuity and the need for overlapping windows, thus enhancing the integrity and consistency of the imputation results.
Imputation
The imputation component of Selphi utilizes a modified version of the Li Stephens HMM14,21. In Selphi’s adaptation of HMM, the hidden states, which are not directly observable, are represented by haplotypes at specific loci across the genome, denoted by pairs of indices (m,n), with m indexing the haplotype within the reference panel and n designating the particular genetic marker in question.
Our method diverges from the standard use of the forward-backward algorithm for imputation, primarily because of how we define transition probabilities. We permit a complete transition probability for a move from one hidden state to a subsequent state, provided that the haplotype’s position in the reference panel remains consistent (this condition is depicted as Hm + 1 = Hm). Hm stands for a hidden state at marker index m. Here, hidden state refers to a specific haplotype in the reference panel of haplotypes, and m is the index of that haplotype in the reference panel. In this condition we allow the model to have a full transition probability (equal to 1) from one state to another state when the haplotype does not change from one marker to the next.
The exact probability of such transitions is outlined in equation (3), where Ne denotes the effective population size, which is typically assumed to be 1,000,000. dm signifies the recombination distance, which we derive through linear interpolation of the distances provided by a publicly available genetic map (genetic map). Finally, NumHid corresponds to the total number of hidden states.
The forward-backward algorithm is used to estimate the probabilities of missing genetic marker data. This process has been optimized by implementing the forward-backward algorithm using sparse matrices for both forward and backward passes, which considerably reduces computational load. The transition probabilities are then used to infer the most likely haplotypes given the observed genotypes.
For computational efficiency, Selphi processes each haplotype in parallel, dedicating a computing core to each target haplotype. This parallel processing extends to the interpolation of reference states, following a method akin to that used in Beagle5.44 and IMPUTE55, where linear interpolation between two boundary probabilities is employed to compute the reference states.
The cumulative probabilities for both the reference and alternate alleles are then computed at each marker, culminating in the imputed genetic profile.
Sparse reference format
Efficient interpolation requires rapid retrieval of selected haplotypes at markers within the interpolation window. Selphi includes a customized tool for compressing large reference panels into chunked sparse matrices, enabling rapid access of reference panel data with a smaller storage footprint than a compressed VCF22. Reference panel haplotypes are converted to sparse matrices, each containing a preset number of markers. The sparse matrices are compressed with Zstandard compression and organized within a zip archive, allowing rapid loading into memory. Once loaded, sparse matrices are cached in memory until they are no longer accessed, eliminating disk latency as Selphi moves down the chromosome. The chunked storage format also allows Selphi to parallelize imputation across the chromosome without loss of performance.
Selphi offers good flexibility by allowing generation of the srp format from both compressed/uncompressed VCF/BCF and XSI reference formats23, enhancing its adaptability to diverse data sources. This versatility empowers Selphi to seamlessly handle various reference data types. The .srp format’s inherent flexibility streamlines the process, ensuring smooth and reliable imputation even in scenarios with a large number of samples and when the data size of a compressed VCF reference panel could be problematic to handle.
Datasets
1000 Genomes Project
The 1000 Genomes Project 30x dataset contains phased sequenced data of 3,202 individuals sampled from 26 different populations. We selected all the individuals without relatives in the dataset to test imputation in unrelated individuals. The filtering was executed using the pedigree file available at (http://ftp.1000genomes.ebi.ac.uk/vol1/ftp/technical/working/20130606_sample_info/20130606_g1k.ped). Individuals that had a Family ID that diverged from the Individual ID were selected and used as our reference panel while individuals with the same Family ID and Individual ID were used as the Target dataset for imputation. This filtering ensures that there are no related individuals between the Target and Reference panel that could inflate imputation results. The number of samples in the reference panel was 2401. The final number of target samples was 801, belonging to 12 out of the 26 populations found in the dataset (Supplementary Fig. 1). All analysis used the hc-WGS 30x version of the 1000 Genomes Project (1KG)16.
We used the following filtering criteria for all variants: (i) only variants with FILTER=PASS were retained; (ii) variants with genotype missingness below 5% were included; (iii) variants passing the Hardy-Weinberg equilibrium (HWE) test, indicated by an HWE P value greater than 10-10 in at least one of the five super-populations, were kept; (iv) variants with a Mendelian error rate of 5% or lower were considered; and finally, (v) variants with a minor allele count (MAC) of 2 or higher were included.
To assess imputation accuracy we masked a portion of the markers to simulate genotyping data. We limited the 1000 Genomes reference data to markers that had at least one minor allele copy in the reference panel, and we masked markers not found on the Illumina GSA chip array (Supplementary table 4). This masking process was applied to all chromosomes using the GSA chip array as reference (GSA v3 by Illumina).
TOPMed
To compare imputation performance against a more diverse reference panel, we assembled a larger, ethnically and ancestrally diverse reference panel using hc-WGS data from 32 studies (48 consensus groups; Supplementary table 5) available through the NHLBI TOPMed (Trans-Omics for Precision Medicine) Program17, encompassing 90,897 participants. We considered the Freeze 8, GRCh38 version of TOPMed data, which is the latest version with all consent groups bearing the same number of variants. For details regarding the processing of TOPmed Freeze 8, see (https://topmed.nhlbi.nih.gov/topmed-whole-genome-sequencing-methods-freeze-8). TOPMed data were made available as gVCF files through the database of Genotypes and Phenotypes (dbGaP). We focused on chromosome 20 and performed haplotype phasing using Beagle5.45, which is particularly optimized for large datasets like TOPMed.
From the TOPMed dataset, we selected a subset of 5,000 samples, coming from the Multi-Ethnic Study of Atherosclerosis (MESA)24,25 for our imputation experiments. MESA is a significant medical research study investigating subclinical cardiovascular disease across various ethnic groups (White-Caucasian 1634, Black-African-American 930, Hispanic 862, Chinese-American 535). These selected samples were unrelated to each other within the dataset. The remaining 85,897 hc-WGS samples from the TOPMed dataset served as a comprehensive reference panel.
The quality control (QC) steps were executed as follows: Initially, we split multi-allelic variants into bi-allelic forms using BCFtools26. The subsequent filtering of SNPs and indels was based on several criteria: (i) a Hardy-Weinberg equilibrium P value less than 10-30, (ii) more than 5% missing data among individuals (based on a GQ score = 0), (iii) abnormal heterozygosity rates, defined as less than 0.5 or greater than 1.5, (iv) alternative alleles with an AA-score below 0.5, (v) variants where the FILTER field was not ’PASS’, (vi) kept only biallelic SNPs. These QC measures are crucial for ensuring the reliability of subsequent analyses and were automated within the TOPMed data processing framework.
A total of 46 phased VCF files – one for each consensus group, excluding two from MESA - were then merged. The final reference panel for chr20 thus assembled consisted of 85,897 samples and 17,900,635 biallelic SNPs. The reference was also converted into formats appropriate for each imputation tool (.bref3 format for Beagle5, .m3vcf for minimac4 and imp5 for IMPUTE5). For imputation validation, we used genotype data derived from a masking of MESA samples, using the GSA SNP array.
UK Biobank
We used the 150,119 hc-WGS data jointly called with GraphTyper v2.7.127, available as pVCF files on the UK Biobank RAP28. We selected all autosomal chromosomes and conducted haplotype phasing using Shapeit v4.2.229. The quality control process was carried out as follows: initially, multi-allelic variants were decomposed into bi-allelic variants using BCFtools26.
Subsequently, SNPs and indels were filtered based on several criteria: (i) a Hardy-Weinberg P value lower than 10-30, (ii) over 5% of individuals with missing data (GQ score = 0), (iii) an excess of heterozygosity, measured as less than 0.5 or greater than 1.5, (iv) alternative alleles with an AA-score below 0.5, and (v) variant sites where the FILTER tag did not match PASS. We selected a subset of 50,000 samples with White British ancestry from the UK Biobank dataset. These samples were unrelated to any other individual in the dataset and had Axiom SNP array data available for imputation experiments, making them the target samples. The remaining 100,119 hc-WGS samples from the UK Biobank were utilized as the reference panel. Phased Axiom genotype data have been downloaded from the UK Biobank study conducted by Clare Bycroft et al. (2018)19. Subsequently, the data was lifted over to the GRCh38 human reference genome, with strand flips discarded, resulting in a dataset comprising 657,354 autosomal markers for 487,442 samples (Supplementary table 6). After liftover, approximately 99.8% of the original variants were retained for further analysis.
Benchmarking
We analyzed the autosomal chromosomes from the 1KG reference panel to explore the distribution of the selected states in our imputation experiments. The 801 unrelated target samples were imputed against the remaining haplotypes in the reference panels. We compared the accuracy of Selphi with the most up-to-date versions of Beagle5.44, IMPUTE55 and Minimac46 and used default parameters for each program. We used the true genetic map for analyses for Beagle5.4, IMPUTE5 and Selphi for real data imputation. Minimac4 does not require a genetic map, as recombination parameters are estimated and stored when producing the m3vcf format input file for the reference data.
The accuracy of the methods was assessed by comparing the imputed allele probabilities to the true (masked) alleles, as previously described7. Markers were binned into bins according to the minor allele frequency of the marker in the reference panel. For each bin we also calculated the squared correlation (r2) between the vector of all the true (masked) alleles and the vector of all posterior imputed allele probabilities, the number of errors in concordance with the true masked allele, and Precision and Recall as the F-score30,31. For the imputation accuracy evaluation, we have rebuilt a faster version of the tool Simpy7 to obtain all evaluation metrics. All imputation analyses for the 1000 Genomes Project (1KG) were conducted on an AWS EC2 instance featuring a 107-vCPU computer equipped with Intel Xeon Platinum 8171M CPU processors and 753 GB of memory.
For the TOPMed dataset, we focused our analysis solely on chromosome 20 for efficacy, following the same exact methodology stated previously. All computations for TOPMed were performed at Scripps HPC (High Performance Computing) facility through a Singularity image32, using a variable number of 16-CPU nodes equipped with 128Gb RAM.
For the UK Biobank (UKB) dataset, a similar approach was employed. The imputation experiments were conducted on the UKB RAP platform. To execute Selphi on the UKB RAP platform, our software was developed as a single applet on the DNAnexus platform. These applets were run with distinct hardware configurations, employing virtual machines (VMs) tailored to meet the minimum hardware requirements specific to each chromosome being imputed.
GWAS analysis
Following the imputation of all autosomal chromosomes for the entire cohort of 50,000 individuals of white British ancestry from the UK Biobank, we selected 50 phenotypes (Supplementary table 7) with less than 10% missing data across anthropomorphic traits and blood measurements in our call set for further analysis. To assess associations between the selected phenotypes and the imputed call sets, we utilized plink233 with default parameters, incorporating sex, age, and the first 10 principal components (PCs) as covariates. We analyzed the hc-WGS dataset, along with two datasets imputed by Beagle 5.4 and Selphi. Our locus selection criteria involved two key factors: (i) we focused on genome-wide significant loci with P values less than 5e-08 reported by the NHGRI Catalog of published GWAS (release 2023-08-26)34, and (ii) we considered the strongest signal per locus (±100 kb genomic region) to select independent loci. For the analysis, we exclusively considered imputed variants, removing those present in the axiom array. To compare beta values (slope) and P values (significance) between the imputed set and the results obtained with the hc-WGS set, we adopted two approaches: (1) using absolute beta values and (2) employing the negative logarithm of the P value on a logarithmic scale to address low and highly significant P values (for at least nominally significant associations, P < 0.05). In evaluating concordance (r2) in the correlation of imputed vs. hc-WGS association values, we assessed how well the data fit the 1:1 identity line.
PRS analysis
In the final phase of our study, we utilized seven GWAS phenotypes mentioned earlier to generate PRS scores, including atrial fibrillation, asthma, hypertension, type 2 diabetes, height, apolipoprotein B levels, and calcium. To facilitate the analysis, quantitative traits were transformed into binary categories: short stature was defined as the lowest 10% of individuals based on height, accounting for sex; hypercalcemia was characterized by calcium levels exceeding 2.6 mmol/L; and high ApoB was designated for levels surpassing 1.3 g/L. We generated summary statistics by meta-analyzing existing external datasets collected by the GWAS Catalog (Supplementary table 8). We implemented clumping plus thresholding models, exploring various parameter values as detailed by Privé et al. (2019)35. Specifically, we investigated squared correlation thresholds of clumping within {0.01, 0.05, 0.1, 0.2, 0.5, 0.8, 0.95}, base sizes of clumping windows within {50, 100, 200, 500} divided by r2 of clumping (parameter 1), a sequence of 50 thresholds on P values between the least and most significant values on a log-log scale, and 13 minor allele frequency (MAF) threshold filters ranging from 0.001 to 0.1. During the training phase, we assessed a total of 18,200 PRS models per phenotype and selected the most accurate one for each callset as the optimal hyperparameters. The 50,000 individuals from the UK Biobank (UKBB), utilized in the GWAS power analysis, were divided into 30,000 for training and 20,000 for testing the PRS models. The assessment of PRS accuracy involved two key measures: (i) relative risk, defined as the ratio of the percentage of cases found between the fifth quintile (individuals with high PRS) and the first quintile (individuals with low PRS) of the PRS distribution; and (ii) area under the curve (AUC).
Acknowledgments
We thank the team and our colleagues at Omics Edge and Genius Labs. This research was conducted by using the UK Biobank Resource under application number 84038.
Footnotes
No changes
