Estimating Disorder Probability Based on Polygenic Prediction Using the BPC Approach

Emil Uffelmann, Major Depressive Disorder Working Group of the Psychiatric Genomics Consortium, Schizophrenia Working Group of the Psychiatric Genomics Consortium, Alkes L. Price, Danielle Posthuma, Wouter J. Peyrot
doi: https://doi.org/10.1101/2024.01.12.24301157

Abstract

Polygenic Scores (PGSs) summarize an individual’s genetic propensity for a given trait in a single value, based on SNP effect sizes derived from Genome-Wide Association Study (GWAS) results. Methods have been developed that apply Bayesian approaches to improve the prediction accuracy of PGSs through optimization of estimated effect sizes. While these methods are generally well-calibrated for continuous traits (implying the predicted values are on average equal to the true trait values), they are not well-calibrated for binary disorder traits in ascertained samples. This is a problem because well-calibrated PGSs are needed to reliably compute the absolute disorder probability for an individual to facilitate future clinical implementation. Here we introduce the Bayesian polygenic score Probability Conversion (BPC) approach, which computes an individual’s predicted disorder probability using GWAS summary statistics, an existing Bayesian PGS method (e.g. PRScs, SBayesR), the individual’s genotype data, and a prior disorder probability. The BPC approach transforms the PGS to its underlying liability scale, computes the variances of the PGS in cases and controls, and applies Bayes’ Theorem to compute the absolute disorder probability; it is practical in its application as it does not require a tuning dataset with both genotype and phenotype data. We applied the BPC approach to extensive simulated data and empirical data of nine disorders. The BPC approach yielded well-calibrated results that were consistently better than the results of another recently published approach.

Introduction

Polygenic Scores (PGSs)1 are per-individual estimates of the total contribution of common genetic variants to a trait or disorder liability based on SNP effect sizes (betas) from Genome-Wide Association Studies (GWAS)2. While summarizing an individual’s genetic risk for a disorder in a single value has the potential to be a simple and informative metric, PGS applications are limited because they are generally only interpretable at the group level. Accordingly, PGSs are commonly evaluated using the coefficient of determination (R2)3 or the Area Under the Curve (AUC)4, metrics that are blind to the scale of the PGS. Moreover, risk estimates based on PGSs are often reported in terms of quantiles (e.g. a PGS falls in the top 5% of a given distribution), which can be difficult to interpret in terms of personal absolute risk of disease.

To make PGSs directly interpretable to individuals, they can be transformed into probabilities. For example, if an individual receives a PGS of 0.5 for multiple sclerosis, then this should correspond to a 50% probability of that individual developing multiple sclerosis in their lifetime. With access to a sufficiently large population-representative tuning sample with relevant pheno- and genotype data, such a transformation can be achieved with existing methods5,6. However, in most clinical settings, such samples are not readily available. Ideally, a single individual’s genotype data and publicly available resources should be sufficient to achieve such a transformation.

Bayesian PGS methods are known to be well-calibrated for continuous traits7–9, meaning the slope equals 1 when regressing the true phenotype on the PGS (implying the predicted values are on average equal to the true trait values). This offers a unique opportunity to achieve well-calibrated probabilities for binary disorder traits. However, when samples are over-ascertained for cases, Bayesian PGSs can become miscalibrated and therefore require a transformation.

Here, we introduce Bayesian polygenic score Probability Conversion (BPC), an approach to transform PGSs based on Bayesian methods (e.g. PRScs8 and SBayesR7), that only requires a single individual’s genotype data, GWAS summary statistics, and a prior disorder probability. We confirm that the resulting probabilities are well-calibrated in simulations and empirical analyses of nine disorders and that the BPC approach performs better than a recently published approach10.

Methods

Bayesian polygenic score Probability Conversion (BPC) approach

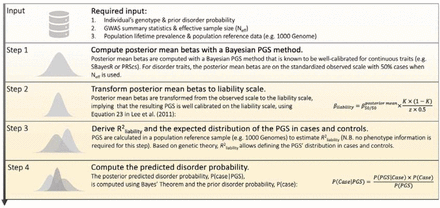
We developed the BPC approach to achieve calibration for binary disorder traits in ascertained samples, using the existing Bayesian Polygenic Score (PGS) methods PRScs8 and SBayesR7. The BPC approach follows four steps (see Figure 1).

Figure 1.
Figure 1. Overview of the Bayesian polygenic score Probability Conversion (BPC) approach.

The BPC approach transforms an individual’s Polygenic Score (PGS) into a well-calibrated disorder probability. See the glossary for the definition of key terms.

Input

First, the BPC approach requires as input an individual’s genotype data and prior disorder probability (see Discussion for how to set the prior). Second, the BPC approach requires the GWAS results (training sample) summary statistics and the effective sample size (Neff) of the training sample (i.e. sum of Neff of all cohorts contributing to the meta-analysis12). Third, the population lifetime prevalence of the disorder of interest, and ancestry-matched population reference data (e.g. 1000G) is required. No tuning dataset with both genotype and phenotype data is required. We note, that instead of individual-level population reference data, summary-level LD and allele frequency information could in principle be used as well.

Step 1 Compute posterior mean betas with a Bayesian PGS method

The BPC approach requires the posterior mean betas to be on the standardized observed scale with 50% case ascertainment (β50/50). For PRScs, this is achieved by simply using Neff (i.e. the effective sample size)12 as input because PRScs is based on the GWAS Z-scores, noting that 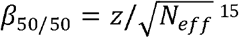Embedded Image. In contrast, SBayesR is based on the GWAS effect sizes (typically on the log-odds scale), which βrst need to be transformed to Embedded Image before applying SBayesR, while also setting Neff as sample size.

Step 2 Transform posterior mean betas to liability scale

The posterior mean betas are transformed from the standardized observed scale with 50% case ascertainment to the continuous liability scale (βliability)14 : Embedded Image where K denotes the disorder population lifetime prevalence and z is the height of the standard normal probability density function at a threshold corresponding to K14. Subsequently, a PGS is constructed using βliability and an individual’s genotype data.

Step 3 Derive R2liability and the expected distribution of the PGS in cases and controls

To define the standard normal probability density function of the PGS in both cases and controls, an estimate of R2liability, the coefficient of determination on the liability scale3, is required. When a PGS is well-calibrated for a standardized phenotype with variance 1 (here the liability16), the variance of the PGS equals the variance explained by the PGS in the phenotype: 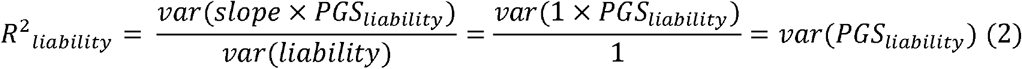Embedded Image where slope refers to the regression of the liability on PGSliability (which is equal to 1 due to the PGS being well-calibrated). Thus, R2liability can be estimated by computing va,(PGSliability) in an ancestry-matched population reference sample without the need for phenotype data. Given R2liability, the expected mean and variance of the PGS can be estimated in cases and in controls using normal theory17,18. Thus, the expected conditional probabilities P(PGsi |ni = case) and P(PGsi|ni = control) can be estimated for every individual i with PGS value PGsi and disease status Di.

Step 4 Compute the genetically informed disorder probability

Finally, we use Bayes’ theorem to update the prior disorder probability to the posterior probability: 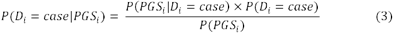Embedded Image where P(Di = case) is the prior disorder probability for individual i, P(PGSi|Di = case) is the conditional probability, and P(PGsi) is the normalization factor corresponding to P(PGsi|Di = case) x P(ni = case) P(PGsi |Di = control) x (1 -P(ni = case)). Thus, the BPC approach provides predicted disorder probabilities for individuals based on GWAS summary statistics, individual genotype data, and a prior disorder probability. (See Code Availability for R code to implement the BPC approach.)

Alternative approaches to obtain disorder probabilities from PGS

The BPC approach transforms a single individual’s genotype data to the predicted disorder probability based on only publicly available data, without requiring tuning data that include both pheno- and genotype data, making it practical in its application. We are aware of only one other published approach that computes disorder probabilities only based on publicly available data, introduced in Pain et al. (2022)10. In addition, we describe the linear rescaling approach an unpublished alternative to the BPC approach.

Briefly, the approach of Pain et al. (2022)10 works as follows. First, the difference in mean PGS between cases and controls is computed based on an estimate of the R2 (which is transformed to the AUC19,20), assuming the PGS have the same variance in cases and controls (scaled to 1). The R2 is estimated based on the GWAS summary statistics using lassosum21. Second, the PGS distribution across cases and controls is divided into quantiles, and third, the disorder probabilities per PGS quantile are assessed based on the testing sample’s case-control ratio (i.e. the prior disorder probability). For individual i, the predicted disorder probability follows by finding which quantile contains its PGS Z-value (standardized based on the distribution of the PGS in 1000 Genomes).

The approach of Pain et al. (2022) differs in three important ways from the BPC approach. First, it implicitly assumes that the variance and the mean of the PGS in the full population are the same as in the target sample. However, if the target sample is over-ascertained for cases, the variance and the mean are larger than in the full population (see Figure S1). As such, PGS Z-values based on the full population (i.e. 1000 Genomes) will overestimate the PGS Z-values in the ascertained target sample, and consequently also the predicted disorder probabilities. Second, Pain et al. (2022) suggest using lassosum21 to estimate the R2 from summary statistics, while the BPC approach achieves this by estimating the variance of a well-calibrated PGS in a population reference sample (see Methods: Derive R2 liability and the expected distribution of the PGS in cases and controls). Third, the Pain et al. (2022) approach assumes var,(PGS|case) = var,(PGs|control), while the BPC approach models more precisely the fact that var,(PGS|case) < var,(PGS|control), which has the most impact for disorders with low population lifetime prevalence (K) and large 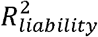Embedded Image values (see Results & Table S1 for a summary of these differences).

We developed an alternative approach, the linear rescaling approach, to obtain well-calibrated predicted disorder probabilities, that does not apply Bayes’ Theorem but a linear rescaling of the PGSliability instead. The linear rescaling approach follows steps 1-3 of the BPC approach as described above and in Figure 1. Subsequently, the expected variance of the PGSliability in the ascertained sample, var,(PGSliability| ascertained sample), is computed based on the prior disorder probability (i.e. the case-control ratio in the testing sample, P(case)) and the distribution of PGSliability in cases and controls (see Methods: Derive R2liability and theexpected distribution of the PGS in cases and controls). Next, the PGS is scaled to PGS’ with the property that Embedded Image in the ascertained sample (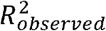Embedded Image is computed based on R2liability and the transformation introduced in Lee et al. (2012)3), resulting in PGS’ that is well-calibrated on the standardized observed scale (see Equation 2). Lastly, we scale the PGS’ (which is based on a standardized phenotype) to the observed scale with cases coded 1 and controls Embedded Image, resulting in PGSs that represent the predicted disorder probability. We note the linear rescaling approach can lead to predicted disorder probabilities that are larger than 1 and smaller than 0, which we truncate to 1 and 0 before evaluating its calibration.

Untransformed PGS

We also evaluated the calibration of untransformed PGSs. These are constructed using the posterior mean betas of step 1 (see Figure 1 and Methods: Step 1 Compute posterior mean betas with a Bayesian PGS method), which are on the standardized observed scale with 50% case ascertainment when Neff is used as input in the Bayesian PGS methods. The resulting PGSs are centered around 0 and cannot be interpreted as disorder probabilities.

Metrics of performance

To assess calibration, we compute the Integrated Calibration Index (ICI): the weighted average of the absolute difference between the real disorder probability and the predicted disorder probability11. (The real disorder probability is computed using the loess smoothing function in R; thus, the ICI can be intuitively understood as the weighted difference between the calibration curve and the diagonal line in a calibration plot (see Results)). Lower values of the ICI indicate better calibration and perfect calibration implies ICI=0.

The calibration slope is another metric to assess calibration that is often used in the literature7–9, which refers to the slope from a linear regression of the phenotype of interest on the PGS. If the slope equals 1 and the intercept 0, the predictor is said to be well-calibrated. A downside of this metric is that a PGS with values outside the range of 0 and 1 can still have a calibration slope of 1, and the ICI has been proposed as a superior and more robust metric11. Typically, untransformed Bayesian PGSs are centered around 0, and while they may have a calibration slope of 1, they cannot be interpreted as disorder probabilities and cannot be evaluated with the ICI.

To assess the prediction accuracy of the PGSs, we use the Area Under the Curve (AUC) and the coefficient of determination (R2) (we note the AUC and R2 can be transformed into one another3).

Simulation analysis

We simulated individual-level data for 1,000 SNPs in linkage equilibrium based on the threshold model13 (see Supplemental note for details). We repeated the simulations 100 times for eight different parameter settings where we varied the power of the training sample and thereby the coefficient of determination (R2liability) of the PGS (R2liability = {0.01, 0.05, 0.10, 0.15}), as well as the disorder population lifetime prevalence (K = {0.01, 0.15}). The disorder’s SNP-based heritability was set to 0.2. We simulated three independent samples: a training sample with case-control information used to estimate SNP effects with a GWAS (varying N; see below), a population reference sample without case-control information to estimate R2liability as described above (N = 503), and a testing sample with case control-information to evaluate model performance (Ncase=1,000 and Ncontrol=1,000). To achieve the desired R2liability in the testing sample, we approximated the required sample size of the training sample using the avengeme package in R22 (e.g. Ntraining = 2,759 when R2liability = 0.1 and K = 0.01). We computed the posterior mean betas using Bpred, the version of LDPred that assumes linkage equilibrium9, with GWAS betas on the standardized observed scale with 50% case ascertainment and therefore used Neff as input. We applied the BPC approach to estimate predicted disorder probabilities and compared it to the existing approach introduced in Pain et al. (2022)10.

Empirical analysis

We analyzed nine phenotypes based on large training samples of GWAS meta-analyses, namely schizophrenia (SCZ)23, major depression (MD)24, breast cancer (BC)25, coronary artery disease (CAD; we note that 23% of the training sample included individuals from non-European populations)26, inflammatory bowel disease (IBD)27, multiple sclerosis (MS)28, prostate cancer (PC)29, rheumatoid arthritis (RA)30, and type 2 diabetes (T2D)31. We computed the PGSs in three testing datasets that were fully independent of the respective training datasets (Table 1). For SCZ and MD, 62 and 22 testing cohorts, respectively, were used, and PGSs were computed based on the GWAS results that excluded the testing cohort form the Psychiatric Genomics Consortium (PGC). In evaluating the ICI, we concatenated all individual cohorts. Testing data from the UK Biobank32 was used for BC, CAD, IBD, MS, PC, RA, and T2D. If SNP-wise Neff values were available in the GWAS results, the maximum Neff across all SNPs was used as input to the BPC approach (MD and SCZ). Alternatively, Neff was calculated as the sum of Neff of all contributing cohorts (CAD, IBD, MS, RA)12. If neither information was available, the SNP-wise Neff were estimated analytically with Embedded Image, where AF = effect allele frequency and SE = standard error (PC, BC). Because the analytically derived Neff can produce large outliers, we used the 90th percentile across all SNPs instead of the maximum as input to the BPC approach.

View this table:
Table 1. Phenotype Summary

PGC-MD = Major Depression Working Group of the Psychiatric Genomics Consortium; PGC-SCZ = Schizophrenia Working Group of the Psychiatric Genomics Consortium; UKB = UK Biobank

Standard quality control was applied: Ambiguous (i.e. A/T or C/G SNPs), duplicate, and mismatching alleles for SNPs across training, testing, and population reference sample were removed1; a minor allele frequency filter of 10% and when available an imputation INFO filter of 0.9 was applied as described before34; The major histocompatibility complex (MHC) was removed (hg19 coordinates: 6:28000000:34000000).

Posterior mean betas of SNPs were computed with PRScs-auto8 (from here on simply referred to as PRScs; version June 4th, 2021) and SBayesR (version 2.03)7. PRScs uses a Linkage Disequilibrium (LD) reference panel based on HapMap335 SNPs and Europeans from the 1000 Genomes Project36 (the default for PRScs). We use the default parameters listed on the software’s GitHub page (see Web resources). In the input of PRScs, we specified the sample size as Neff to ensure posterior mean betas were on the standardized observed scale with 50% case ascertainment (see Step 1 Compute posterior mean betas with a Bayesian PGS method). SBayesR uses an LD reference panel that is based on HapMap335 SNPs and 50,000 European UK Biobank subjects (the default for SBayesR version 2.03). In the input for SBayesR, we transformed the effect sizes to the standardized observed scale with 50% case ascertainment 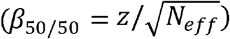Embedded Image and set the sample size to Neff (see Step 1 Compute posterior mean betas with a Bayesian PGS method).

To estimate R2liability we use an ancestry-matched population reference sample, namely the European sample of 1000 Genomes36 (see Methods: Derive R2liability and the expected distribution of the PGS in cases and controls), which we downloaded from the MAGMA website (see Web resources).

The posterior mean betas were used to compute the PGS in 1000 Genomes and in the testing sample with Plink1.9 (version Linux 64-bit 6th June, 2021; command “--score <variant ID column> <effect allele column> <posterior mean beta> sum center”; see Data and Code Availability).

The BPC approach requires a valid estimate of the prior disorder probability, which we set to the case-control ratio in the testing sample (see Discussion for approaches to estimate the prior disorder probability). We ascertain cases in the testing sample such that the case-control ratio is equal to 25%, 50%, or 75%.

Results

Simulation analysis

We evaluated the BPC approach and Pain et al. (2022) across different values of R2liability (1%, 5%, 10%, and 15%), and population lifetime prevalences (1% and 15%) in 100 simulation runs (see Figure 2). Across all parameter combinations, the BPC approach consistently achieves mean ICI values close to 0 (ranging from mean 0.014 (± SE 0.0004) to 0.017 (± 0.0006) across 4×2=8 parameter settings), meaning the predicted and observed probabilities agree closely.

Figure 2.
Figure 2. Calibration in simulations.

Calibration of the BPC and the Pain et al. (2022) approach was evaluated using the Integrated Calibration Index (ICI) in 100 simulation runs and for combinations of two parameters, the population lifetime prevalence (K), and the explained variance of the PGS on the liability scale (R2liability). The BPC approach achieves low mean ICI values in every condition, while the mean ICI values of the Pain et al. (2022) approach are consistently larger. The difference between both approaches becomes larger for conditions with low population lifetime prevalences and large R2liability values. Error bars represent standard errors.

The Pain et al. (2022) approach performs considerably less well (ranging from 0.039 (± 0.002) to 0.118 (± 0.009) across all parameter settings; see Figure 2) because it does not distinguish the prior disorder probability (in this case the testing sample case-control ratio) from the lifetime prevalence in the full population, which overestimates the predicted probabilities and negatively impacts calibration (see Methods: Alternative approaches to obtain disorder probabilities from PGS for details and Figure S1 for a schematic representation). Indeed, the distinction between the BPC and Pain et al. (2022) approach is more pronounced when the disorder population lifetime prevalence is low, because this increases the difference between the population lifetime prevalence and the prior disorder probability (which is set to 50%). Similarly, larger values of R2liability exacerbate the overestimates of the Pain et al. (2022) approach because it leads to more power to detect the bias (except for R2liability = 1%; see below). A simple adaptation of the Pain et al. (2022) approach to take both the population lifetime prevalence and prior disorder probability into account strongly improves its calibration and removes the negative impact of the low population lifetime prevalence and increasing R2liability values; nevertheless, the BPC approach continues to achieve lower ICI values (see Figure S2). For low simulated values of R2liability, when the discovery GWAS has little power, the R2liability values estimated with lassosum in the Pain at al. (2022) approach become unstable (see below), leading to an increased ICI. When we adjust the Pain et al. (2022) approach to take both the population lifetime prevalence and prior disorder probability into account and compute the variance of a well-calibrated PGS in a population reference sample to estimate R2liability (instead of lassosum), the difference between both approaches becomes very small (see Figure S3). Nonetheless, the BPC approach achieves slightly better calibration in nearly every condition, because the Pain et al. (2022) approach assumes that the variance of the PGS is the same in cases and controls, while they are different and the difference becomes larger for higher R2liability values and lower population lifetime prevalences (see Figure S4 and Methods: Alternative approaches to obtain disorder probabilities from PGS).

In addition to the ICI, we used the calibration slope and intercept to evaluate calibration. Again, the BPC approach consistently achieves good calibration (see Figures S5 and S6) and performs better than the Pain et al. (2022) approach. However, we note the calibration slope for Pain et al. (2022) implies nearly perfect calibration when the population lifetime prevalence is low and Embedded Image is large, while the ICI implies strong miscalibration due to overestimated predicted probabilities (see Figure 2), which illustrates that the regression slope can be a poor measure for the calibration of probabilities11.

We also evaluated our linear rescaling approach (see Methods: Alternative approaches to obtain disorder probabilities from PGS). We found that the linear rescaling approach performs reasonably well but worse than the BPC approach, because it can result in probabilities that are larger than 1 and lower than 0. This mostly occurs in conditions where the population lifetime prevalence is low and Embedded Image is large. Setting these outlying values to 1 and 0, respectively, negatively impacts calibration (see Figure S7). Therefore, our primary recommendation is to use the BPC approach.

Lastly, we found that the calibration slopes of untransformed Bayesian PGSs for binary disorder traits deviate from 1 in ascertained samples, even when the case-control ratios in the training and testing sample are both 50% and the PGSs are on the standardized observed scale with 50% case ascertainment. Similarly, the calibration intercepts deviate from 0 (see Figure S8, S9; the bias is most apparent when the population lifetime prevalence is low and 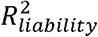Embedded Imageis large). This is because the transformation from the to the observed scale in ascertained samples is linear for the GWAS results (i.e. betas) used to compute the PGS14 but non-linear for the coefficient of determination (R2 liability) of the PGS3 (see Figure S10). As a result,var,(PGSobserved) and 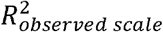Embedded Image are not proportional, and the PGSs can thus not be well-calibrated (see equation 2) without a probability conversion approach. Untransformed PGS do attain accurate calibration when neither the training nor the testing sample case-control ratios differ from the population lifetime prevalence (i.e. random ascertainment), even when the population lifetime prevalence is low (K = 0.01) and 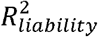Embedded Imageis large (0.15) the PGS’s mean calibration slope over 100 simulation runs does not significantly differ from 1 (mean calibration slope = 1.02, s.e.m. = 0.02). We note that the untransformed Bayesian PGSs are centered around 0, and can therefore not be evaluated with the ICI11.

Empirical analysis

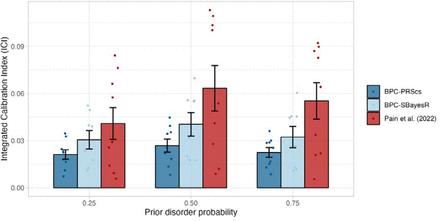
To further evaluate the performance of the BPC approach, we applied it to nine phenotypes across nine training datasets (SCZ23, MD24, BC25, CAD26, IBD27, MS28, PC29, RA30, and T2D31) and three testing datasets (i.e. UK Biobank32, PGC-SCZ23, PGC-MD24; see Methods: Empirical analysis and Table 1 for a summary). We ascertained cases and controls for each phenotype such that the testing sample case-control ratios were 0.25, 0.5, and 0.75. We performed similar comparisons as in the simulations with the addition of two applications of the BPC approach, one using PRScs8 (BPC-PRScs) and one using SBayesR7 (BPC-SBayesR) to compute posterior mean betas (see Figure 1 and Methods: Bayesian polygenic score Probability Conversion (BPC) approach). We note that for SBayesR, the results did not converge for prostate cancer and therefore depict one fewer data point. Results are reported in Figure 3 and Table S2. Averaged across all prior disorder probabilities, BPC-PRScs achieves the lowest mean ICI value of 0.024 (± 0.002), followed by BPC-SBayesR with 0.034 (± 0.004). The Pain et al. (2022) approach has the largest mean ICI value of 0.053 (± 0.007). The BPC-PRScs approach consistently achieves the lowest mean ICI values across all prior disorder probabilities. We note the Pain et al. (2022) approach can be used with both PRScs and SBayesR. While the presented results are based on PRScs, using SBayesR yields comparable results (see Figure S11 and Table S2).

Figure 3.
Figure 3. Calibration in empirical analyses of nine disorders.

Calibration of the BPC and the Pain et al. (2022) approach was evaluated using the Integrated Calibration Index (ICI) for nine disorders, while varying the prior disorder probability. The BPC approach was applied using two Bayesian PGS methods, PRScs (BPC-PRScs) and SBayesR (BPC-SBayesR). The BPC-PRScs approach achieves the lowest mean ICI values across all prior disorder probabilities. BPC-SBayesR shows one fewer data points, as it did not converge for prostate cancer. Numerical values are presented in Table S2. Error bars represent standard errors.

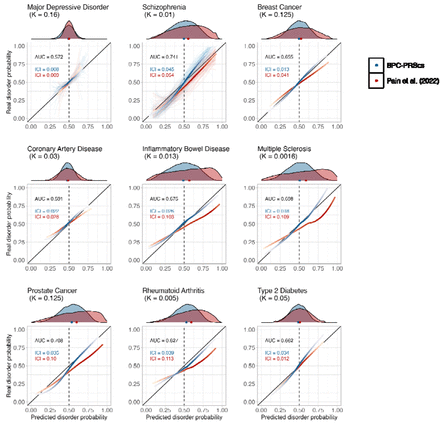
When focusing in detail on the calibration plots with a prior disorder probability of 50%, BPC-PRScs shows better calibration than the Pain et al. (2022) approach for every trait, except Type 2 Diabetes (see Figure 4 and Table S2). The Pain et al. (2022) approach tends to overestimate the probabilities for many traits, as can be seen by the right shift of the histograms and calibration lines. This is particularly true for traits with low population lifetime prevalence and large values, such as rare auto-immune disorders (i.e. Inflammatory Bowel Disorder, Multiple Sclerosis, and Rheumatoid Arthritis) and Prostate Cancer, which is in line with our theoretical expectations (see Methods: Alternative approaches to obtain disorder probabilities from PGS and Figure S1 for a schematic representation).

Figure 4.
Figure 4. Disorder-specific calibration curves in empirical analyses of nine disorders.

Calibration of the BPC and the Pain et al. (2022) approach was evaluated using the Integrated Calibration Index (ICI) for nine disorders, each with a prior disorder probability of 0.5 (see Table 1 for an overview of the case/control testing sample sizes). The prior disorder probability was set to 0.5, as opposed to the lifetime prevalence in the general population (K), to emulate the higher risk of help-seeking individuals in clinical settings. Histograms at the top of the plots depict the distribution of the predicted disorder probabilities, and the dots at the base of the histograms depict the mean predicted probability. The lines were drawn with a loess smoothing function, and their transparency follows the density of the histogram to show which parts of the distribution carry the most weight in the calculation of the ICI. For major depression and schizophrenia, 62 and 22 cohorts, respectively, were available for analysis and therefore depict thin, light-colored, and transparent lines for individual cohorts. In contrast, the thicker and darker lines depict results when data from all cohorts are concatenated. The disorder population lifetime prevalence (K) is reported. The Area Under the receiver operator Curve (AUC) is the same for both approaches because the transformations do not change the ranking of individual PGSs, and both approaches use the same PGS inputs. The BPC-PRScs approach achieves lower ICI values for eight out of nine disorders. The Pain et al. (2022) approach tends to overestimate the predicted disorder probabilities, as seen by the right shift of the histograms and the dots. Numerical values are presented in Table S3. Calibration curves for BPC-SBayesR are presented in Figure S12.

We performed secondary analyses yielding the following six conclusions. First, comparing the calibration plots of BPC-PRScs with BPC-SBayesR, the latter makes correct predictions on average but is less well-calibrated for low and high values of the predicted disorder probabilities (see Figure S12 and Table S2). Second, misspecification of the effective sample size by a factor of 0.5 and 2 negatively impacts calibration for BPC-PRScs, while it does not affect the calibration of the Pain et al. (2022) approach (see Figure S13 and Table S3) as it involves a scaling step after the posterior mean betas have been computed. We note the BPC approach still has lower median ICI values than the Pain et al. (2022) approach. BPC-SBayesR seems generally more robust to misspecification of the effective sample size, except for Coronary Artery Disease which suffers extreme miscalibration when Neff is multiplied by 2. Third, including the MHC region strongly and negatively impacts calibration for the autoimmune disorders Multiple Sclerosis and Rheumatoid Arthritis for BPC-PRScs and Pain et al. (2022) (but not BPC-SBayesR; This is because SBayesR’s reference sample excludes most of the MHC region; see Figures S14 and Table S4). Fourth, reducing the INFO filter from 0.9 to 0.3 and the minor allele frequency filter from 10% to 1% (as in34) yields comparable average ICI values (except for Coronary Artery Disease and BPC-SBayesR; see Figure S15 and Table S5). Fifth, evaluating calibration with the slope and intercept from a linear regression of the phenotype on the predicted disorder probabilities also shows that BPC-PRScs is best calibrated overall (see Figures S16, S17, and Table S6).

In contrast to simulations (see Figure S8), the untransformed Bayesian PGSs do not show strongly miscalibrated slopes (see Figure S18), likely due to the variance of estimates of the calibration slopes in combination with much fewer observations in empirical data (i.e. 9) than in simulations (100 simulation runs for 8 parametrizations). Our findings are in line with the previous observation that the calibration slope is very sensitive to miscalibration in small parts of the data and that the ICI is more robust and preferred as a metric for calibration11. Because untransformed Bayesian PGSs are centered around 0 and do not range from 0 to 1, they cannot be evaluated with the ICI, and cannot be interpreted as predicted disorder probabilities.

Estimation of variance explained (R2liability)

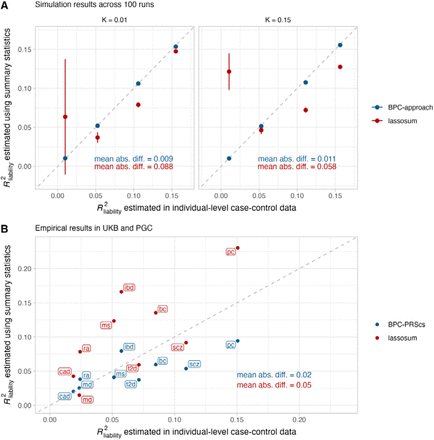
The BPC approach depends on a valid estimate of R2liability. Our approach of computing the variance of a well-calibrated PGS in a population reference sample without the need for phenotype data (see Methods: Step 3 Derive R2liability and the expected distribution of the PGS in cases and controls) leads to estimates that are very close to the observed values from linear regression3 in a sample with both pheno- and genotype data in simulations (mean absolute difference ranges from 0.009 to 0.011; see Figure 5A) and in empirical data (mean absolute difference = 0.02; see Figure 5B). The Pain et al. (2022) approach uses lassosum21, which leads to estimates are slightly misspecified in simulations (mean absolute difference ranges from 0.058 to 0.088) and in empirical data (mean absolute difference = 0.05).

Figure 5.
Figure 5. Embedded Image estimates in simulations and empirical analyses of nine disorders.

(A)Simulation results of estimating 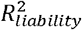Embedded Image using the BPC approach and lassosum (as used by Pain et al. (2022)), both of which do not require disorder-specific individual-level genotype and phenotype data. The x-axis depicts 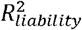Embedded Image estimated by regressing disorder status on the Bayesian PGS in individual-level data in the testing sample3. Error bars depict standard errors for 100 simulation runs. The grey dashed line depicts the identity line when y = x. The BPC approach achieves mean estimates that are closer to the regression results in the testing sample in every simulation condition. mean abs. diff. = mean absolute difference of 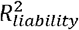Embedded Image estimates using summary statistics and individual-level case-control data. (B)Empirical results in the UKB and PGC of estimating 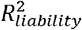Embedded Image using the BPC-PRScs approach and lassosum. The BPC-PRScs approach achieves estimates that are closer to the regression results in the testing sample on average (mean absolute difference of 0.02 vs. 0.05).

Discussion

We developed the BPC approach to transform PGSs to absolute risk values, which yields predicted disorder probabilities that may be clinically useful for single individuals. Based on Bayesian PGS methods, it requires only minimal input, namely GWAS summary statistics, a single individual’s genome-wide genotype data and prior disorder probability, and an estimate of the disorder’s population lifetime prevalence. We verified in simulations and empirical analyses of nine disorders that the BPC approach achieves good calibration, meaning the predicted and real disorder probabilities closely align. The BPC approach depends on a valid estimate of R2 liability, which we compute by estimating the variance of a well-calibrated PGS in a population reference sample without the need for phenotype data, and verify that the estimates are close to empirically calculated values in case-control data.

We compared the BPC approach to a recently published approach in Pain et al. (2022)10, and showed that it achieves lower ICI values in every simulation condition and for eight out of nine tested disorders in empirical analyses. This is partly because the Pain et al. (2022) approach overestimates the predicted disorder probabilities whenever the prior disorder probability exceeds the population lifetime prevalence.

In clinical settings where a single individual may be considered, the prior disorder probability, which can be interpreted as the case-control ratio in a hypothetical testing sample to which that individual belongs, can be approximated in several ways. It may be estimated using external data to obtain a data-informed prior, such as context-specific lifetime prevalence estimates of individuals seeking health care for a specific disorder in a given hospital. The context may refer to any variable that modifies a disorder’s lifetime prevalence, such as age, sex, or income37, meaning any covariate can be incorporated into the prior disorder probability. Alternatively, if no data is available, prior elicitation38 may be used, where a clinician (or a panel of clinicians) provides a subjective estimate of the prior. Generally, the lifetime risk for help-seeking individuals is expected to be higher than for individuals from the general population (where lifetime risk = K). As such, the prior will often be higher than K.

There are several limitations to this study. First, because most GWASs are based on individuals from European populations, the calibration of the BPC approach for individuals from non-European populations is unknown but may be negatively affected, as is the accuracy of risk predictions39,40. However, as long as the GWAS population matches that of the individual, the BPC approach is expected to be well-calibrated. Future studies are needed to develop methods to obtain well-calibrated predictions for individuals from non-European populations. Second, the potential for clinical utility of polygenic prediction (and thereby the BPC approach) strongly depends on the magnitude of the PGS’s R2liability, which is currently prohibitively small for most traits. However, there are some traits, such as cardiovascular disease and type 2 diabetes, for which current PGSs may already be sufficiently powered to find clinical application41–43 and be economically effective44–49. Moreover, as GWAS sample sizes grow, the PGS’s R2liability is expected to approach the disorder’s h2SNP, and therefore their clinical applicability will become more likely. Third, the calibration of the predicted disorder probabilities depends on a correct estimate of the prior for a typical polygenic GWAS trait. Future studies may explore a two-step approach by using well-calibrated conventional risk prediction models to inform the prior disorder probability, which in turn may then be used in the BPC approach. Fourth, the BPC can only be applied to polygenic traits with normally distributed PGSs. For autoimmune disorders, we show that the inclusion of the MHC region, which harbors outlying large-effect variants, can negatively impact calibration. Similarly, rare variants cannot currently be incorporated into the BPC approach. However, this is also true for the Bayesian PGS methods the BPC approach is based on. Integrating prediction based on rare variants with large effects with polygenic prediction is an important direction for future research.

In conclusion, the BPC approach provides an effective tool to compute well-calibrated predicted disorder probabilities based on polygenic scores.

Data Availability

Individual-level data from the Psychiatric Genomics Consortium (https://pgc.unc.edu/) and the UK Biobank (https://www.ukbiobank.ac.uk/enable-your-research/apply-for-access) cannot be shared freely, but an access application is required first. The GWAS summary statistics used in the UKB analyses can be requested or downloaded from the following web pages: Breast Cancer (https://bcac.ccge.medschl.cam.ac.uk/bcacdata/oncoarray/oncoarray-and-combined-summary-result/gwas-summary-associations-breast-cancer-risk-2020/); BMI (https://portals.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files); Coronary Artery Disease (http://www.cardiogramplusc4d.org/data-downloads/#); Inflammatory Bowel Disease (https://www.ibdgenetics.org/); Multiple Sclerosis (https://imsgc.net/?page_id=31); Prostate Cancer (http://practical.icr.ac.uk/blog/?page_id=8164); Rheumatoid Arthritis (https://data.cyverse.org/dav-anon/iplant/home/kazuyoshiishigaki/ra_gwas/ra_gwas-10-28-2021.tar); Type 2 Diabetes (https://diagram-consortium.org/downloads.html). GWAS summary statistics for Major Depression and Schizophrenia can be downloaded from the PGC website (https://pgc.unc.edu/for-researchers/download-results/). 1000 Genomes reference files can be downloaded from https://ctg.cncr.nl/software/magma.

Declaration of interests

The authors declare no competing interests.

Author contributions

Emil Uffelmann: Methodology, Software, Formal analysis, Investigation, Data Curation, Writing - Original Draft, Visualization

Alkes Price: Writing - Review & Editing

Danielle Posthuma: Writing - Review & Editing, Funding acquisition, Supervision Wouter J. Peyrot: Conceptualization, Methodology, Software, Resources, Writing – Original Draft and Review & Editing, Supervision

Data and code availability

Scripts to apply the BPC approach can be downloaded from https://github.com/euffelmann/bpc. Individual-level data from the Psychiatric Genomics Consortium (https://pgc.unc.edu/) and the UK Biobank (https://www.ukbiobank.ac.uk/enable-your-research/apply-for-access) cannot be shared freely, but an access application is required first. The GWAS summary statistics used in the UKB analyses can be requested or downloaded from the following web pages: Breast Cancer (https://bcac.ccge.medschl.cam.ac.uk/bcacdata/oncoarray/oncoarray-and-combined-summary-result/gwas-summary-associations-breast-cancer-risk-2020/); BMI (https://portals.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files); Coronary Artery Disease (http://www.cardiogramplusc4d.org/data-downloads/#); Inflammatory Bowel Disease (https://www.ibdgenetics.org/); Multiple Sclerosis (https://imsgc.net/?page_id=31); Prostate Cancer (http://practical.icr.ac.uk/blog/?page_id=8164); Rheumatoid Arthritis (https://data.cyverse.org/dav-anon/iplant/home/kazuyoshiishigaki/ra_gwas/ra_gwas-10-28-2021.tar); Type 2 Diabetes (https://diagram-consortium.org/downloads.html). GWAS summary statistics for Major Depression and Schizophrenia can be downloaded from the PGC website (https://pgc.unc.edu/for-researchers/download-results/).

1000 Genomes reference files can be downloaded from https://ctg.cncr.nl/software/magma.

Acknowledgments

We thank Naomi Wray, Peter Visscher, and Oliver Pain for their helpful discussions. D.P. is supported by the Netherlands Organization for Scientific Research—Gravitation project ‘BRAINSCAPES: A Roadmap from Neurogenetics to Neurobiology’ (024.004.012) and the European Research Council advanced grant ‘From GWAS to Function’ (ERC-2018-ADG 834057). The PGC has received major funding from the US National Institute of Mental Health (PGC4: R01MH124839, PGC3: U01 MH109528; PGC2: U01 MH094421; PGC1: U01 MH085520). A.L.P has received an R01 grant from the US National Institutes of Health (HG006399). We thank the participants who donated their time, life experiences, and DNA to this research and the clinical and scientific teams that worked with them. We are deeply indebted to the investigators who comprise the PGC. Statistical analyses were carried out on the NL Genetic Cluster Computer (http://www.geneticcluster.org) hosted by SURFsara. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

References

  1. 1.↵
    Choi, S. W., Mak, T. S.-H. & O’Reilly, P. F. Tutorial: a guide to performing polygenic risk score analyses. Nat. Protoc. 1–14 (2020) doi:10.1038/s41596-020-0353-1.
    OpenUrlCrossRefPubMed
  2. 2.↵
    Uffelmann, E. et al. Genome-wide association studies. Nat. Rev. Methods Primer 1, 1–21 (2021).
    OpenUrlCrossRef
  3. 3.↵
    Lee, S. H., Goddard, M. E., Wray, N. R. & Visscher, P. M. A better coefficient of determination for genetic profile analysis. Genet. Epidemiol. 36, 214–224 (2012).
    OpenUrlCrossRefPubMed
  4. 4.↵
    Wray, N. R., Yang, J., Goddard, M. E. & Visscher, P. M. The Genetic Interpretation of Area under the ROC Curve in Genomic Profiling. PLoS Genet. 6, e1000864 (2010).
    OpenUrlCrossRefPubMed
  5. 5.↵
    Sun, J. et al. Translating polygenic risk scores for clinical use by estimating the confidence bounds of risk prediction. Nat. Commun. 12, 5276 (2021).
    OpenUrl
  6. 6.↵
    Ashenhurst, J. R. et al. A Generalized Method for the Creation and Evaluation of Polygenic Scores. (2021).
  7. 7.↵
    Lloyd-Jones, L. R. et al. Improved polygenic prediction by Bayesian multiple regression on summary statistics. Nat. Commun. 10, 5086 (2019).
    OpenUrl
  8. 8.↵
    Ge, T., Chen, C.-Y., Ni, Y., Feng, Y.-C. A. & Smoller, J. W. Polygenic prediction via Bayesian regression and continuous shrinkage priors. Nat. Commun. 10, 1776 (2019).
    OpenUrl
  9. 9.↵
    Vilhjálmsson, B. J. et al. Modeling Linkage Disequilibrium Increases Accuracy of Polygenic Risk Scores. Am. J. Hum. Genet. 97, 576–592 (2015).
    OpenUrlCrossRefPubMed
  10. 10.↵
    Pain, O., Gillett, A. C., Austin, J. C., Folkersen, L. & Lewis, C. M. A tool for translating polygenic scores onto the absolute scale using summary statistics. Eur. J. Hum. Genet. 1–10 (2022) doi:10.1038/s41431-021-01028-z.
    OpenUrlCrossRef
  11. 11.↵
    Austin, P. C. & Steyerberg, E. W. The Integrated Calibration Index (ICI) and related metrics for quantifying the calibration of logistic regression models. Stat. Med. 38, 4051–4065 (2019).
    OpenUrl
  12. 12.↵
    Grotzinger, A. D., Fuente, J. de la Privé, F., Nivard, M. G. & Tucker-Drob, E. M. Pervasive Downward Bias in Estimates of Liability-Scale Heritability in Genome-wide Association Study Meta-analysis: A Simple Solution. Biol. Psychiatry 93, 29–36 (2023).
    OpenUrl
  13. 13.↵
    Falconer, D. S. The inheritance of liability to certain diseases, estimated from the incidence among relatives. Ann. Hum. Genet. 29, 51–76 (1965).
    OpenUrlCrossRefWeb of Science
  14. 14.↵
    Lee, S. H., Wray, N. R., Goddard, M. E. & Visscher, P. M. Estimating missing heritability for disease from genome-wide association studies. Am. J. Hum. Genet. 88, 294–305 (2011).
    OpenUrlCrossRefPubMedWeb of Science
  15. 15.
    Peyrot, W. J. & Price, A. L. Identifying loci with different allele frequencies among cases of eight psychiatric disorders using CC-GWAS. Nat. Genet. 53, 445–454 (2021).
    OpenUrlCrossRef
  16. 16.↵
    Falconer, D. S. & Mackay, T. F. C. Introduction to quantitative genetics. (Pearson, Prentice Hall, 2009).
  17. 17.↵
    Tallis, G. M. Ancestral covariance and the Bulmer effect. Theor. Appl. Genet. 73, 815–820 (1987).
    OpenUrlCrossRef
  18. 18.↵
    Peyrot, W. J., Boomsma, D. I., Penninx, B. W. J. H. & Wray, N. R. Disease and Polygenic Architecture: Avoid Trio Design and Appropriately Account for Unscreened Control Subjects for Common Disease. Am. J. Hum. Genet. 98, 382–391 (2016).
    OpenUrlCrossRefPubMed
  19. 19.↵
    Rice, M. E. & Harris, G. T. Comparing effect sizes in follow-up studies: ROC Area, Cohen’s d, and r. Law Hum. Behav. 29, 615–620 (2005).
    OpenUrlCrossRefPubMedWeb of Science
  20. 20.↵
    Aaron, B., Kromrey, J. D. & Ferron, J. Equating ‘r’-based and ‘d’-based Effect Size Indices: Problems with a Commonly Recommended Formula. https://eric.ed.gov/?id=ED433353 (1998).
  21. 21.↵
    Mak, T. S. H., Porsch, R. M., Choi, S. W., Zhou, X. & Sham, P. C. Polygenic scores via penalized regression on summary statistics. Genet. Epidemiol. 41, 469–480 (2017).
    OpenUrl
  22. 22.
    Dudbridge, F. Power and Predictive Accuracy of Polygenic Risk Scores. PLOS Genet. 9, e1003348 (2013).
    OpenUrlCrossRefPubMed
  23. 23.↵
    Trubetskoy, V. et al. Mapping genomic loci implicates genes and synaptic biology in schizophrenia. Nature 604, 502–508 (2022).
    OpenUrlPubMed
  24. 24.↵
    Wray, N. R. et al. Genome-wide association analyses identify 44 risk variants and refine the genetic architecture of major depression. Nat. Genet. 50, 668–681 (2018).
    OpenUrlCrossRefPubMed
  25. 25.↵
    Zhang, H. et al. Genome-wide association study identifies 32 novel breast cancer susceptibility loci from overall and subtype-specific analyses. Nat. Genet. 52, 572–581 (2020).
    OpenUrlCrossRefPubMed
  26. 26.↵
    Nikpay, M. et al. A comprehensive 1000 Genomes–based genome-wide association meta-analysis of coronary artery disease. Nat. Genet. 47, 1121–1130 (2015).
    OpenUrlCrossRefPubMed
  27. 27.↵
    Liu, J. Z. et al. Association analyses identify 38 susceptibility loci for inflammatory bowel disease and highlight shared genetic risk across populations. Nat. Genet. 47, 979–986 (2015).
    OpenUrlCrossRefPubMed
  28. 28.↵
    INTERNATIONAL MULTIPLE SCLEROSIS GENETICS CONSORTIUM. Multiple sclerosis genomic map implicates peripheral immune cells and microglia in susceptibility. Science 365, eaav7188 (2019).
    OpenUrlAbstract/FREE Full Text
  29. 29.↵
    Schumacher, F. R. et al. Association analyses of more than 140,000 men identify 63 new prostate cancer susceptibility loci. Nat. Genet. 50, 928–936 (2018).
    OpenUrlCrossRefPubMed
  30. 30.↵
    Ishigaki, K. et al. Multi-ancestry genome-wide association analyses identify novel genetic mechanisms in rheumatoid arthritis. Nat. Genet. 54, 1640–1651 (2022).
    OpenUrlCrossRefPubMed
  31. 31.↵
    Mahajan, A. et al. Fine-mapping type 2 diabetes loci to single-variant resolution using high-density imputation and islet-specific epigenome maps. Nat. Genet. 50, 1505–1513 (2018).
    OpenUrlCrossRefPubMed
  32. 32.↵
    Sudlow, C. et al. UK Biobank: An Open Access Resource for Identifying the Causes of a Wide Range of Complex Diseases of Middle and Old Age. PLOS Med. 12, e1001779 (2015).
    OpenUrlCrossRefPubMed
  33. 33.
    Sullivan, P. F. & Geschwind, D. H. Defining the Genetic, Genomic, Cellular, and Diagnostic Architectures of Psychiatric Disorders. Cell 177, 162–183 (2019).
    OpenUrlCrossRefPubMed
  34. 34.↵
    Ni, G. et al. A Comparison of Ten Polygenic Score Methods for Psychiatric Disorders Applied Across Multiple Cohorts. Biol. Psychiatry S0006-3223(21)01263–4 (2021) doi:10.1016/j.biopsych.2021.04.018.
    OpenUrlCrossRef
  35. 35.↵
    Gibbs, R. A. et al. The International HapMap Project. Nature 426, 789–796 (2003).
    OpenUrlCrossRefPubMedWeb of Science
  36. 36.↵
    Auton, A. et al. A global reference for human genetic variation. Nature 526, 68–74 (2015).
    OpenUrlCrossRefPubMed
  37. 37.↵
    Hou, K., Xu, Z., Ding, Y., Harpak, A. & Pasaniuc, B. Calibrated prediction intervals for polygenic scores across diverse contexts. 2023.07.24.23293056 Preprint at doi:10.1101/2023.07.24.23293056 (2023).
    OpenUrlAbstract/FREE Full Text
  38. 38.↵
    van de Schoot, R. et al. Bayesian statistics and modelling. Nat. Rev. Methods Primer 1, 1–26 (2021).
    OpenUrlCrossRef
  39. 39.↵
    Martin, A. R. et al. Clinical use of current polygenic risk scores may exacerbate health disparities. Nat. Genet. 51, 584–591 (2019).
    OpenUrlCrossRefPubMed
  40. 40.↵
    Ding, Y. et al. Polygenic scoring accuracy varies across the genetic ancestry continuum. Nature 618, 774–781 (2023).
    OpenUrl
  41. 41.↵
    Klarin, D. & Natarajan, P. Clinical utility of polygenic risk scores for coronary artery disease. Nat. Rev. Cardiol. 19, 291–301 (2022).
    OpenUrlCrossRef
  42. 42.
    Khera, A. V. et al. Genome-wide polygenic scores for common diseases identify individuals with risk equivalent to monogenic mutations. Nat. Genet. 50, 1219–1224 (2018).
    OpenUrlCrossRefPubMed
  43. 43.↵
    Billings, L. K. et al. Utility of polygenic scores for differentiating diabetes diagnosis among patients with atypical phenotypes of diabetes. J. Clin. Endocrinol. Metab. dgad456 (2023) doi:10.1210/clinem/dgad456.
    OpenUrlCrossRef
  44. 44.↵
    Martikainen, J. et al. Economic evaluation of using polygenic risk score to guide risk screening and interventions for the prevention of type 2 diabetes in individuals with high overall baseline risk. Front. Genet. 13, 880799 (2022).
    OpenUrl
  45. 45.
    Kiflen, M. et al. Cost-Effectiveness of Polygenic Risk Scores to Guide Statin Therapy for Cardiovascular Disease Prevention. Circ. Genomic Precis. Med. 15, e003423 (2022).
    OpenUrl
  46. 46.
    Mujwara, D. et al. Integrating a Polygenic Risk Score for Coronary Artery Disease as a RisklJEnhancing Factor in the Pooled Cohort Equation: A CostlJEffectiveness Analysis Study. J. Am. Heart Assoc. Cardiovasc. Cerebrovasc. Dis. 11, e025236 (2022).
    OpenUrl
  47. 47.
    Thomas, C. et al. The Costs and Benefits of Risk Stratification for Colorectal Cancer Screening Based On Phenotypic and Genetic Risk: A Health Economic Analysis. Cancer Prev. Res. Phila. Pa 14, 811–822 (2021).
    OpenUrlAbstract/FREE Full Text
  48. 48.
    Pashayan, N., Morris, S., Gilbert, F. J. & Pharoah, P. D. P. Cost-effectiveness and Benefit-to-Harm Ratio of Risk-Stratified Screening for Breast Cancer. JAMA Oncol. 4, 1504–1510 (2018).
    OpenUrl
  49. 49.↵
    Wong, J. Z. Y. et al. Cost effectiveness analysis of a polygenic risk tailored breast cancer screening programme in Singapore. BMC Health Serv. Res. 21, 379 (2021).
    OpenUrl
Back to top
Posted January 13, 2024.
Download PDF

Supplementary Material

Data/Code
Email
Estimating Disorder Probability Based on Polygenic Prediction Using the BPC Approach
Emil Uffelmann, Major Depressive Disorder Working Group of the Psychiatric Genomics Consortium, Schizophrenia Working Group of the Psychiatric Genomics Consortium, Alkes L. Price, Danielle Posthuma, Wouter J. Peyrot
medRxiv 2024.01.12.24301157; doi: https://doi.org/10.1101/2024.01.12.24301157
Twitter logo Facebook logo LinkedIn logo Mendeley logo
Citation Tools

Subject Area