An economic evaluation of routine hepatocellular carcinoma surveillance for high-risk patients using a novel approach to modelling competing risks

1.1 Hepatocellular carcinoma and surveillance

Worldwide, liver cancer is the fourth most common cause of cancer death;[1] in Australia, it is the seventh most common cause of cancer-related death[2] driven by increasing trends in both liver cancer incidence and mortality.[3] A key step to improving mortality outcomes is increased detection at early stages, to improve the potential for curative treatment.[4, 5, 6]

Hepatocellular carcinoma (HCC), the most common form of primary liver cancer, can be detected early through routine HCC surveillance. Routine HCC surveillance is typically recommended for high-risk populations.[7] In Australia, clinical guidelines recommend HCC surveillance with six-monthly ultrasound (US) imaging, with the potential addition of alpha-fetoprotein (AFP) blood testing, for people with compensated liver cirrhosis,[8, 9] and some population groups with chronic hepatitis B.

Determining appropriate HCC surveillance recommendations poses significant challenges, including identifying health benefits and long-term costs,[10] appropriate target groups,[11, 12] and optimal technologies and intervals.[13] This is needed to develop an economic case for health system investment.

1.2 Modelling and HCC

Epidemiological modelling allows a formal synthesis and extrapolation of data to evaluate the impact of an intervention. This approach has been used to guide investment in cancer control interventions.[14, 15, 16, 17, 18] For HCC, models can synthesise data sources such as time to liver decompensation and HCC in patients with cirrhosis[19, 20] and cirrhosis and HCC survival.[21, 22, 2, 23, 24] This can be combined with clinical data on surveillance outcomes and cost data to provide cost-effectiveness estimates. Economic models of HCC and surveillance are less established than for other cancers,[15] but are crucial for guiding policy and investment in liver cancer control.

Internationally, modelling studies have analysed a range of populations and interventions for liver cancer control; reviews have been published previously.[8, 7, 25] Australian modelling has shown that six-monthly US, with or without AFP, is likely cost-effective for patients with cirrhosis,[10] and biomarker testing can stratify risk to improve cost-effectiveness.[26] Further modelling which captures detailed progression of liver disease, operates at flexible timescales, and incorporates detailed survival data could refine recommendations for surveillance algorithms.

There are a number of unique considerations for modelling HCC and liver disease, such as the interaction of competing risks of liver decompensation and other liver disease events,[27, 28] the complex distribution of sojourn times for the development of HCC in cirrhotic patients,[29] significant comorbidities in the target population,[30] and short expected survival times for HCC patients.[31] Simple Markov-style models struggle to capture this complexity, while more complex models such as discrete event simulations[32, 33, 34], agent-based/microsimulation models,[35, 14] and semi-Markov models[36, 37, 38] can be hampered by a lack of data, and typically introduce stochastic elements and increase computation burden. In the absence of detailed health state data, using observable data on the time an individual takes to transition between health states, the sojourn time, can improve model fidelity.

1.3 Approach

To address this, we developed the sojourn time density model framework. We model the dynamics of the probability density of the sojourn time by health state, tracking both the likelihood of being in a given state and the expected time in that state.

The model is parametrised by the cause-specific hazard rates [39, 40] (analogous to transition intensities[38]), allowing us to exploit survival data and methods[41] such as Kaplan-Meier estimators[42, 39, 43] and risk ratios.[44] This captures the same detail as typical survival models, with the addition of serial state transitions, and is analogous to semi-Markov and discrete event simulations, but with a deterministic numerical scheme.

1.4 Aims

In this manuscript we describe the model structure and numerical scheme for sojourn time density models. We develop a health-economic model of liver disease and HCC, and evaluate the benefits and costs routine HCC surveillance through six-monthly liver US, with or without AFP testing, compared to no surveillance. We also provide an analysis of the potential impact of varying surveillance intervals.

The modelling described in this manuscript was developed to inform the Clinical practice guidelines for HCC surveillance for people at high risk in Australia.[8] The development of these guidelines was led by clinicians in the area of liver disease and liver cancer alongside a multi-disciplinary working party, including healthcare and clinical representatives, representatives with lived experience and other community representatives. This group also informed the aims and structure of this economic analysis.

2.1 Sojourn time density modelling

Consider a compartmental model with N possible discrete states labelled 1, 2, …, N, such that at any time t ∈T (typically T = [0, ∞)) an individual belongs to one of these states. We describe not only the likelihood of an individual being in a given state, but also track the distribution of the length of time spent in that state, the sojourn time τ ∈ T.

Doing so describes a continuous-time random process {X_t}_t∈T with discrete state space {1, 2, …, N }. This process is defined such that P (X_t = i) = P (individual in state i at time t). We can equivalently define the jump process {Y_n, T_n}_n=0,1,2,…, such that Y_n = X_t ∀ t ∈ [T_n, T_n+1), Y_n ≠ Y_n+1.[45]

The cause-specific hazard rates depending on both the model time t and sojourn time τ, are the key parameters for the model. These are the instantaneous transition rates for an individual in state i to transition to state j, at time t, given that the individual has spent time τ in i without any transitions (i.e, entered state i at time t − τ). By modelling the distribution of τ, we can capture evolving transition rates. The t dependency can capture temporal trends as well as evolving risk with age a = a₀ + t where a₀ is the age at t = 0. If there is no possible transition between i and j, then λ_i,j = 0.

Formally, the following should hold: Compare this to the equivalent definition for semi-Markov models, Equation (3) in Krol et al, 2015[46]. For convenience assume λ_i,i(t, τ) = 0 (i.e. there are no self-loops).

To track the model state and the sojourn time, we introduce the density functions for the sojourn time for i = 1, 2, …, N. These are the density functions for the sojourn time τ and the state i at time t. Explicitly, the set of functions {f_i(t, τ)}_i=1,2,…,N is a probability density function on the sample space (τ, i) ∈ T × {1, 2, …N }, describing the likelihood of being in a particular state with a particular sojourn time at fixed time t ∈ T.

Then we can define the probability mass of X_t We should expect that i.e. the total mass probability is 1.

Our goal now is to describe the dynamics of f_i(t, τ), and then show this definition satisfies (2) and (5). Let f_i(t, τ) satisfy the partial differential equation with boundary condition The LHS of equation (6) is motivated by the transport equation along lines of constant t − τ, representing the likelihood of remaining in state i while both t and τ increase, while the RHS captures the likelihood of making a transition to a subsequent state. This can be seen by observing that along the directional derivative the likelihood decays proportionally to the hazard rate (see Section 2.2). The boundary condition (7) represents the accumulation of probability mass in state i post-transition. By (5), the initial conditions f_i(0, τ) should satisfy Additionally, (i.e. the model is supported on finite time only; see Section 2.4). For a further discussion of initial conditions, see Appendix C.1.

We now have a complete description of the random process X_t through (4), (6), (7), and appropriate initial conditions. This constitutes what we will call a sojourn time density model. These models resemble semi-Markov processes/Markov renewal processes,[38] as the sequence of transitions is Markov (as the next state depends only on the previous state and transition time) but the time between transitions is not.

We now show that the process defined by (4) is well-defined and driven by the hazards λ_i,j(t, τ) as expected.

Theorem 2.1.

The random process defined by (4) satisfies conditions (2) and (5). Proof. We calculate the derivative of g_i(t), i.e. the rate of change in likelihood of being in state i at time t This satisfies the definition the hazard rate - the likelihood of being in state i decreases proportionally to the hazard of every transition leaving state , and increases for every transition entering state proportional to the weight of those states f_j(t, τ).

Note that i.e. that the total probability mass is conserved. Therefore with initial conditions satisfying equation (9), (5) is satisfied.

If we know that the system enters state i at time t^∗, i.e. (Y_n, T_n) is realised as (i, t^∗) and remains there to at least time t^∗ + τ ^∗ (i.e. T_n+1 − T_n ≥ τ ^∗), this corresponds to for all t ∈ [t^∗, t^∗ + τ ^∗) where δ(t) is the Dirac delta function. Then and for j≠ i In other words, the likelihood of transition out of state i is proportional to the sum of the hazards Σ_j λ_i,j and the likelihood of transition i → j is proportional to λ_i,j. Then by the above. By taking the limit Δt → 0, (2) is satisfied.

2.2 Method of characteristics and survival analysis

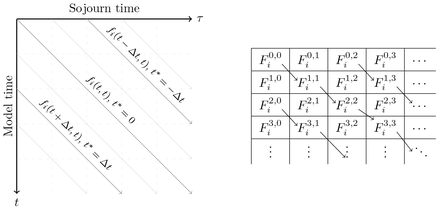
We now compute survival curves using method of characteristics. As noted, equation (6) is best interpreted along characteristics of constant t −τ corresponding to the state entry time (Figure 1). This allows explicit solutions through method of characteristic, as well as analogies to other survival modelling approaches.¹

• Download figure
• Open in new tab

Figure 1.

Characteristics of constant t^∗ = t − τ for f_i(t, τ) (left) and the corresponding elements with constant m − n for the numerical scheme (right).

Consider the characteristic t = t^∗ + τ for fixed t^∗ ∈ ℝ. Then If t^∗ > 0, this corresponds to a characteristic starting from the boundary; if t^∗ ≤ 0, this corresponds to a characteristic from the initial condition. This has solution where t₀ = max(t^∗, 0), τ₀ = max(−t^∗, 0) (so that t^∗ = t₀ − τ₀, t₀, τ₀ ≥ 0) and The function Λ_i(t, τ) is the all-cause cumulative hazard along the characteristic t −τ = t^∗.Then is the all-cause survival along this characteristic, and f_i(t^∗ + τ, τ) = f_i(t₀, τ₀)S_i(t^∗ + τ, τ). We can correspondingly calculate the time-to-event distribution after entering state i at time t − τ as the distribution across j = 1, 2, …, N.

It follows that the probability of the next transition being before time t = t^∗ + τ and also from i → j, given entry to state i at time t₀, is:

P (next transition time < t ∩ next transition i → j | entered state i at time t₀) The limit of this is the likelihood of the next transition being to a particular state:

P (next transition i → j | entered state i at time t₀) We can also calculate the cause-specific survival, assuming other transitions (or events) are censored: Where cause-specific survival data (equivalently, cause-specific cumulative incidence) is available with competing events censored, this may provide a calibration target for the hazard rates, which can be directly identified from the survival model (see Hazard and Cumulative hazard in Clark et al[39]); parametrisation of λ_i,j(t, τ) across t^∗ can then be identified.

Given t^∗, the results above are analogous to the functions used for parametric competing risk survival models, time-to-event models, and discrete event models.[47] The sojourn time density model approach generalises this to modelling serial events deterministically. The all-cause cumulative incidence function 1 −S_i(t, τ) is used in e.g. Fine-Gray modelling.[48] A useful guide to translating between cause-specific and all-cause specific hazard rates is included in Asanjarani et al,[38] and shows discrete event simulation distributions can be translated into hazard rates. For discrete event simulations where events do not preclude each other, transitions which preserve sojourn time may be added (Appendix C.4).

A common approach in analytical epidemiological models is to compute likelihood of transition as the convolution of the τ -dependent hazard rate and the time of entry.[49, 50] In our formulation, this is reflected in the boundary conditions

1. If we define entry time distribution F_j(x) = f_j(x, 0) and survival-adjusted cause-specific hazard rate H(j, i)(x) = λ_j,i(t, x)S_j(t, x), then F_i(t) = Σ_j (F_j ∗H_j,i)(t), the convolution of these. We have generalises this approach and incorporated serial transitions.

2.3 Numerical scheme

The characteristic solutions developed in Section 2.2 can be used to develop a numerical scheme. For a discretisation of T by fixed timesteps Δt ∈ ℝ+, define for m, n ∈ ℤ +. Each value of m − n corresponds to a characteristic (m − n)Δt. The cumulative hazard functions Λ_i(t, τ) may be computed by (20) in simple cases, or estimated iteratively by Δt steps. Equivalently, each element can be calculated iteratively by (see Figure 1 for an illustration of this).

For m < n, the initial condition is For m > 0, the initial condition F^m,0 = f_i(mΔt, 0) is the boundary conditions of the full PDE. A first order scheme can be computed as for m ≥ 0.

One can subsequently approximate and hence the process X_t.

An improvement can be made to this numerical scheme by adjusting the boundary conditions to exactly preserve the total mass at all timesteps: where We can then verify that is constant, i.e. the total probability mass Σ_ig_i(t) is conserved. We have here used the midpoint estimates for λ_i,j, which improves accuracy when there is a significant scale difference between hazards.

In epidemiological contexts, hazards are often modelled as continuous and smooth functions, so this first order numerical scheme will have high accuracy.

2.4 Hazard functions and common parametric distributions

The sojourn time density modelling scheme is determined by the hazard rates λ_i,j(t, τ). It is common to describe these rates parameterically.[51] Commonly used parametric forms for these hazard functions include

• constant hazard λ_i,j(t, τ) = c, corresponding to an exponential time-to-event distribution; if all hazards are constant, X_t is Markov.

• polynomial hazard λ_i,j(t, τ) = bkτ^k−1, corresponding to a Weibull distribution, often used to model single-cause mortality.[52]

• exponential hazard λ_i,j(t, τ) = pe^rτ, corresponding to a Gompertz distribution, often used to model of all-cause mortality.[52]

There are many other potential choices for λ_i,j(t, τ). It may be useful to define the hazard rate piecewise over t, τ, or both, either piecewise constant or functions.[53] The choice of hazard function is highly dependent on the nature of the system being modelled and the available data sources.[54] Hazard rates can be estimated from processed survival data, typically after smoothing[55] or time-to-event distributions.[38, 56]

Hazard can be adjusted to reflect covariates; Cox proportional hazard ratios can be used to calculate λ_i,j(t, τ | x) = λ_i,j(t, τ |0)e^β·x for some covariates x ∈ ℝn and a baseline hazard function λ_i,j(t, τ | 0).[44, 48] Constant hazard multipliers can be used as calibration targets, to maintain the shape of the distribution,[53] and hazards can be adjusted to reflect lead-time biases in the data (see Appendix C.1). With minor alterations, one can also introduce hazards which are dependent on the current state of the system; for example, this allows for modelling of infectious disease models. See Appendix C.3 for further details.

2.5 Example model

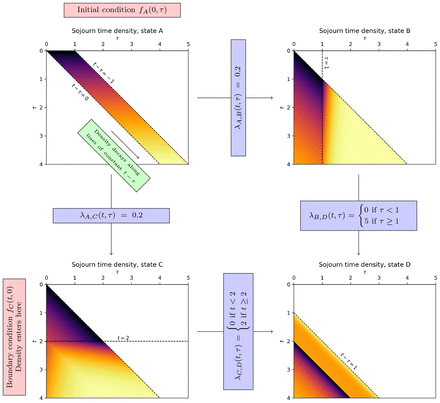
An example sojourn time density model is shown in Figure 2, demonstrating the impact of t- and τ -dependent hazard rates. This model has four states, A, B, C, D. The transitions out of A are λ_A,B(t, τ) = λ_A,C(t, τ) = 0.2, as these are constant, P (X_t = A) decays exponentially, like a Markov process (Figure 3). The subsequent transitions are λ_B,D(t, τ) = 0 if τ < 1, 5 otherwise, and λ_C,D(t, τ) = 0 if t < 2, 2 otherwise. The impact of the t and τ dependencies can be seen in the evolving density of f_i(t, τ). The initial condition was f_A(0, τ) = 1 for τ ∈ [0, 1). Further examples are included in Appendix C.2.

• Download figure
• Open in new tab

Figure 2.

An example sojourn time density model, showing the evolution of the density of sojourn time. Darker regions have higher density, and lighter regions have lower density. Note how the density in state B sharply decreases at τ ≥ 1, and in state C at t ≥ 2. See Figure 3 for the resulting process.

• Download figure
• Open in new tab

Figure 3. The resulting process X_t from the model illustrated in Figure 2

3.1 Model structure

The structure of the model is illustrated in Figure 4. Individuals start with compensated liver cirrhosis, which can develop into decompensated cirrhosis and/or undiagnosed HCC. These states were selected to capture the most clinically-relevant details based on the available data. Undiagnosed HCC is diagnosed either symptomatically/incidentally or at a routine HCC surveillance event. The Australian liver cirrhosis patient population was modelled.

• Download figure
• Open in new tab

Figure 4. A simplified schematic of the model of HCC and liver surveillance.

HCC stage at diagnosis was modelled according to the Barcelona Clinic Liver Cancer (BCLC) staging system,[58] which is based on a patient’s Eastern Cooperative Oncology Group (ECOG) performance status,[59] Child-Pugh Score,[60] and tumour stage. Cancers were identified as early (BCLC stage 0/A: ECOG status 0, tumour ≤3cm), intermediate (BCLC stage B: ECOG status 0, multinodular), or late stage (BCLC stage C/D: ECOG status ≥ 1, vascular invasion, extrahepatic spread, and/or Child-Pugh C). These groupings aligned with available survival data. Patients with compensated cirrhosis initially develop early stage HCC, which can subsequently progress; patients with decompensated cirrhosis develop late stage HCC only. The modelled stage is stage at diagnosis only; post-diagnosis progression is not explicitly modelled, but is reflected in modelling of stage-at-diagnosis survival per the available data.

3.2 Cirrhosis and health state transitions

Decompensation rates for patients with compensated liver cirrhosis were directly available from cohort studies.[61] HCC incidence, diagnosis, and upstaging rates were calibrated based on time-to-event data for HCC diagnosis and observed stage at diagnosis.[61, 62] This was supplemented with data on observed stage at diagnosis in cohorts routinely undergoing HCC surveillance[62] and data on the sensitivity and specificity of HCC surveillance.[63] The full list of sources for the model parameters are included in A.

3.3 HCC and other cause survival

Five-year stage-specific overall survival rates were calculated based on data from the NSW Cancer Registry, as these data are stratified by stage,[64] augmented by national data.[65] International studies were used to inform survival by time since diagnosis, by stage, and screen-vs symptomatically-detected HCC.[24] Treatment modalities, including serial treatments, were not modelled explicitly.

HCC recurrence over five years after initial diagnosis was not modelled due to lack of data; HCC recurrence within five years of the initial diagnosis is included in the modelled five-year survival rates. Other-cause mortality was modelled for people with compensated or decompensated cirrhosis [29] relative to the age-specific mortality rate in Australian data.[66]

3.4 Routine HCC surveillance

HCC surveillance is modelled as routine US with or without AFP after the diagnosis of compensated cirrhosis. Six-monthly US with AFP was modelled as the base case, as currently recommended.[8, 67, 68] Diagnosis to confirm suspected HCC, either after symptomatic development or positive surveillance event (including false positives), was modelled as computed tomography or magnetic resonance imaging, with biopsy in cases where imaging was insufficient.[10] People who experience liver decompensation do not recieve HCC surveillance, per recommendations.[7] For the purposes of this study, patients were assumed to have perfect uptake and adherence to surveillance, to assess the impact of the surveillance recommendations rather than of patient behaviours.

3.5 Costs and health state utilities

The benefits of surveillance were measured in quality-adjusted life-years. Disutilities were identified for patients with compensated cirrhosis, decompensated cirrhosis, and HCC patients. Disutilities for HCC patients were classified according to their phase of care (diagnostic, ongoing, or terminal), as well as multiplicative existing disutilities due to cirrhosis.[69, 70]

Costs and benefits were analysed from a health system perspective to capture the most relevant cost for Australian governmental policymakers, and presented as 2023 Australian dollars with costs adjusted using the Australian health CPI index.[71] Costs relating to cancer treatment were based on an excess-cost study which stratified patients by their primary treatment,[23] which varied by stage at diagnosis. These data were chosen as they are locally relevant and based on real-world observations rather than idealised treatment recommendations.

Costs for surveillance and diagnostic procedures were collated from the Australian Medicare Benefits Schedule. Other costs included annual costs of cirrhosis care for patients with and without decompensation, and end-of-life costs.[72, 73] A lifetime time horizon was included to capture the full downstream benefits of surveillance. For the cost-effectiveness analysis, a 5% annual discount rate was applied to both costs and QALYs, in line with other health economic analyses in Australia.[74] A supplementary sensitivity analysis on the impact of the choice of discount rate was completed. Cost inputs are included in Appendix A.

3.6 Parameters and calibration

Parameters were directly derived or calibrated from relevant sources identified in the clinical guidelines,[8] with Australian studies used where possible. Where Australian trial data were not available, the data sources prioritised meta-analyses with large cohort sizes.

Parametric forms for the hazard rates were chosen to best fit the data while minimising the number of parameters to avoid potential overfitting. Where necessary, the Nelder-Mead algorithm was used to determine the best-fit parameters by minimising the mean square error between the model outputs and the target data. Additional methodology is included in Appendix A.

3.7 Scenarios modelled

For the baseline analysis, we estimated the health benefits and economic impacts of 6-monthly HCC surveillance with US, with or without AFP, with no routine HCC surveillance as the comparator. This was modelled for a cohort with mean age 51 (standard deviation 11) to reflect the general cirrhotic population,[75] by aggregating single-age simulations. We calculated HCC stage, likelihood of HCC death, quality-adjusted life expectancy, and costs. A further analysis was conducted to assess the impact the frequency of surveillance.

3.8 Sensitivity analyses

One-way sensitivity analyses and probabilistic sensitivity analyses were conducted to assess the model’s sensitivity to key parameters. Additional methodology is included in Appendix B.

3.9 Role of the Funders

Financial support for this study was provided by Cancer Council Australia through a contract as part of a project Optimising Liver Cancer Control in Australia which was funded through the Australian Government Department of Health and Aged Care. The funding agreements ensured the authors’ independence in designing the study, interpreting the data, writing, and publishing the report.

4.1 Model calibration

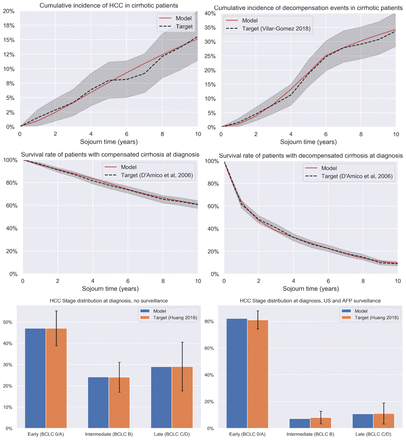
The model was calibrated to reproduce key targets (Figure 5). The model was well-fitted to the target data, reproducing the terminal values for the survival curves and remaining within the 95% confidence intervals for the duration of the survival data. The full parameter set for the model is shown in Appendix A, including calibration targets and parameter distributions used in the sensitivity analyses.

• Download figure
• Open in new tab

Figure 5.

Key calibration outputs. From top to bottom: HCC incidence rates (left; target Vilar Gomez 2018 [61]) and decompensation rates (right); all-cause death rates in patients with compensated (left; includes any decompensation events) and decompensated (right) cirrhosis; HCC stage at diagnosis with (left) and without (right) routine HCC surveillance.

4.2 Health benefits and cost-effectiveness of surveillance

The results of the analysis are shown in Table 1. These analyses were for a cirrhotic cohort with no decompensation, and a mean age of 51 ±11 years. Among those diagnosed with HCC, the probability of being diagnosed at early-stage disease would increase by 81.3% for those that undergo six-monthly US surveillance with AFP.

Six-monthly HCC surveillance with US alone would reduce a person with cirrhosis’ likelihood of HCC death by 21.7% compared to no intervention, increasing the quality-adjusted life-expectancy by 6.2%. Six-monthly US with the addition of AFP would reduce likelihood of HCC death by 22.9%, increasing the quality-adjusted life-expectancy by 6.5%. On average, people with cirrhosis would experience 17.6 surveillance events over their lifetime, and have an average total cirrhosis and HCC costs of 136,324 (2023 AUD), a 5.6% increase compared to those who do not undergo surveillance, with similar increases with the addition of AFP.

The cost-effectiveness of HCC surveillance with six-monthly US would be 33,850/QALY compared to no surveillance, below the indicative willingness-to-pay threshold of 50,000/QALY often used in Australia. This indicates that surveillance using six-monthly US would be cost-effective. Six-monthly surveillance with US and AFP would have a very similar cost-effectiveness of 36,860/QALY compared to no surveillance and be cost-effective. The incremental cost-effectiveness ratio of US with AFP vs US alone would be $81,360/QALY, indicating it is unlikely to be an incrementally cost-effective compared to offering US only.

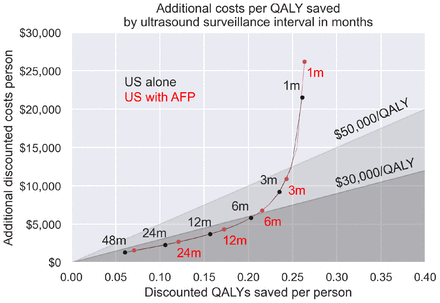
The impact of varying the interval for routine US is shown in Figure 6. Shorter surveillance intervals have higher benefits, but at correspondingly higher costs. Surveillance intervals of 7 months or longer had cost-effectiveness ratio under 30,000/QALY for US with or without AFP. Additional benefits and costs are in very similar proportions at intervals over 12 months, while shorter intervals led diminishing benefits per cost increase. The addition of AFP was approximately equivalent to extending the surveillance interval by 1-3 months.

• Download figure
• Open in new tab

Figure 6.

Discounted costs vs discounted QALYs saved for routine ultrasound surveillance with alpha-fetoprotein by surveillance interval in months, from 1 month to 48 months.

The results of the one-way sensitivity analysis found that the cost-effectiveness was most sensitive to parameters regarding early-stage HCC, including 5-year survival for Stage 0/A HCC and the proportion of HCCs diagnosed at Stage 0/A. The probabilistic sensitivity analysis found that six-monthly US was cost-effective in the 85.5% of simulations, demonstrating that this result is robust to parameter uncertainty. The analysis of the discount rate found that lower discount rates led to more favourable cost-effectiveness, due to the long-term benefits of surveillance. The full results are included in Appendix B.