A multi-task convolutional deep learning method for HLA allelic imputation and its application to trans-ethnic MHC fine-mapping of type 1 diabetes

Tatsuhiko Naito, Ken Suzuki, Jun Hirata, Yoichiro Kamatani, Koichi Matsuda, Tatsushi Toda, Yukinori Okada
doi: https://doi.org/10.1101/2020.08.10.20170522

Abstract

Conventional HLA imputation methods drop their performance for infrequent alleles, which reduces reliability of trans-ethnic MHC fine-mapping due to inter-ethnic heterogeneity in allele frequency spectra. We developed DEEP*HLA, a deep learning method for imputing HLA genotypes. Through validation using the Japanese and European HLA reference panels (n = 1,118 and 5,112), DEEP*HLA achieved the highest accuracies in both datasets (0.987 and 0.976) especially for low-frequency and rare alleles. DEEP*HLA was less dependent of distance-dependent linkage disequilibrium decay of the target alleles and might capture the complicated region-wide information. We applied DEEP*HLA to type 1 diabetes GWAS data of BioBank Japan (n = 62,387) and UK Biobank (n = 356,855), and successfully disentangled independently associated class I and II HLA variants with shared risk between diverse populations (the top signal at HLA-DRβ1 amino acid position 71; P = 6.2 ×10−119). Our study illustrates a value of deep learning in genotype imputation and trans-ethnic MHC fine-mapping.

Introduction

Genetic variants of the major histocompatibility complex (MHC) region at 6p21.3 contribute to the genetic of a wide range of human complex traits.1 Among the genes densely contained in the MHC region, human leukocyte antigen (HLA) genes are considered to explain most of the genetic risk of MHC.1 Strategies for direct typing of HLA alleles, including sequence specific oligonucleotide (SSO) hybridization, Sanger sequencing, and next-generation sequencing, do not easily scale for large cohorts since they are labor-intensive, time-consuming, expensive, and limited in terms of allele resolution and HLA gene coverage.2,3 As a result, in many cases, the genotypes of HLA allele are indirectly imputed from single nucleotide variant (SNV)-level data using population-specific HLA reference panels.3–6

The MHC region harbors unusually complex sequence variations and haplotypes that are specific to individual ancestral populations; thus, the distribution and frequencies of the HLA alleles are highly variable across different ethnic groups.1,7 This causes heterogeneity in reported HLA risk alleles of human complex diseases across diverse populations.8 For example, in type I diabetes (T1D), the strong association between non-Asp57 in HLA-DQβ1 and T1D risk has been found in Europeans9,10 but not in the Japanese population, where the T1D susceptible HLA-DQβ1 alleles carry Asp57.11 Although elucidation of risk alleles beyond ethnicities would contribute to further understanding of genetic architecture of the MHC region associated with pathologies of complex diseases, few trans-ethnic MHC fine-mappings have been reported yet.12 One of the ways of conducting trans-ethnic fine-mapping in the comprehensive MHC region is to newly construct a large HLA reference panel which captures the complexities of the MHC region across different populations.13 The other is to integrate data of different populations which are imputed with a reference panel specific for each population. Although the latter way seems straightforward, we need an HLA imputation method accurate enough for infrequent alleles to robustly evaluate HLA variants which are highly heterogenous in allele frequency across ethnicities.

Various methods for HLA allelic imputation have been developed. SNP2HLA is one of the standard software, which uses the imputation software package Beagle to impute both HLA alleles and the amino acid polymorphisms for those classical alleles.14 HLA Genotype Imputation with Attribute Bagging (HIBAG)15 is also promising software, which employs multiple expectation-maximization-based classifiers to estimate the likelihood of HLA alleles. While SNP2HLA explicitly uses reference haplotype data, of which public accessibility is often limited, HIBAG does not require them once the trained models are generated. Both methods have achieved high imputation accuracy;16 however, are less accurate for rare alleles as shown later. Given the complex linkage disequilibrium (LD) structures specific for the MHC region, a more sophisticated pattern recognition algorithm beyond simple stochastic inference seems to be necessary to overcome this situation.

After boasting of its extremely high accuracy in image recognition, deep learning has been attracting attention in various fields, and a lot of successful applications in the field of genomics have been reported.17 It can learn a representation of input data and discover relevant features of high complexity through deep neural networks. Its typical application for genomic problems is the prediction of the effects of non-coding and coding variants, where the models encodes the inputs of flanking nucleotide sequence data.18–21 Another example is non-liner unsupervised learning of high-dimensional quantitative data of transcriptome.22,23 However, successful representation learnings for SNV-data in the field of population genetics has been limited.24 Here, we developed DEEP*HLA, a multi-task convolutional deep learning method to accurately impute genotypes of HLA genes from SNV-level data. Through application to the two HLA reference panels of different populations, DEEP*HLA achieved higher imputation accuracy both in sensitivity and specificity than conventional methods. Notably, it was more advantageous especially in imputing low frequent or rare alleles. As also a value of our method, it was by far the fastest in total processing time, which indicates its applicability to biobank-scale data. We applied the trained models of DEEP*HLA to the large-scale T1D GWAS data of BioBank Japan (BBJ) and UK Biobank (UKBB), and conducted trans-ethnic HLA association analysis.

Results

An overview of our study

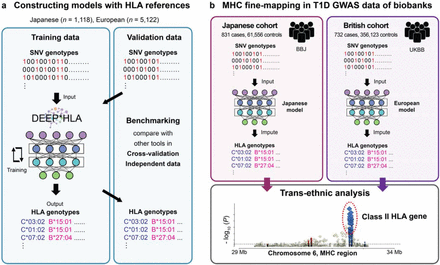
An overview of our study is presented in Fig. 1. Our method, DEEP*HLA, is convolutional neural networks which learn an HLA referenced panel, and impute genotypes of HLA genes from pre-phased SNV data. Its framework uses a multi-task learning which can learn and impute alleles of several HLA genes which belong to the same group simultaneously (see Method). Multi-task learning is presumed to have two advantages in this situation. First, the genotypes of some flanking HLA genes, which often have strong LD for each other, are correlated; and the shared features of individual tasks would be informative. Second, it helps reduce the processing time by grouping tasks especially in our latest reference panel, which consists of more than thirty HLA genes. For robust benchmarking, we targeted the two different HLA imputation reference panels: (i) our Japanese reference panel (n = 1,118);3 (ii) the Type 1 Diabetes Genetics Consortium (T1DGC) reference panel (n = 5,112),25 respectively. We evaluated its performance in comparison with other HLA imputation methods by 10-fold cross-validation and an independent HLA dataset (n = 908).6 In the latter part, we performed MHC fine-mappings of Japanese cohort from BBJ and British cohort from UKBB by applying the trained models specific for individual populations. We integrated the imputed GWAS genotypes and performed trans-ethnic HLA association analysis.

Figure 1.
Figure 1. An overview of the study

(a) Our method, DEEP*HLA, is a deep learning architecture that takes an input of genotypes of SNVs and outputs the genotype dosages of HLA genes. To train a model and benchmark its performance, we used Japanese and European HLA reference panels respectively, and evaluated its accuracies in cross-validation with compared to other tools. In the Japanese panel, we also evaluated its accuracy by applying the trained model to the independent Japanese HLA data. (b) We conducted trans-ethnic MHC fine-mapping in T1D GWAS data of BBJ and UKBB. We performed HLA imputation for the Japanese cohort from BBJ and the British cohort from UKBB using the models specific for individual populations, respectively. We integrated the individual results of imputed genotypes and performed trans-ethnic association analysis.

DEEP*HLA achieved high imputation accuracy especially in low-frequency or rare alleles

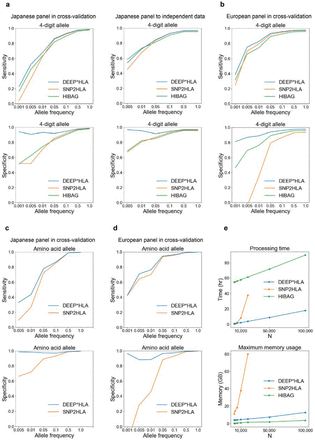
First, we applied DEEP*HLA to the Japanese panel, which is a high-resolution allele catalog of the 33 classical and non-classical HLA genes in 1,118 individuals of Japanese ancestry.3 We compared imputation accuracy of DEEP*HLA in sensitivity and specificity (see Method) with SNP2HLA and HIBAG in 10-fold cross-validation. DEEP*HLA achieved sensitivity and specificity of 0.987 in 4-digit allelic resolution, which were superior to SNP2HLA (sensitivity of 0.985 and specificity of 0.984) and HIBAG (sensitivity and specificity of 0.979; Supplementary Table 1). Remarkably, DEEP*HLA was best through all ranges of allele frequencies; and was more advantageous as alleles were low frequent or rare (Fig. 2a and Supplementary Table 1). In addition to the cross-validation, to investigate whether DEEP*HLA could impute well when applied to independent samples, we applied the model trained with our Japanese reference panel to a dataset of 908 Japanese individuals (1,816 haplotypes) with 4-digit resolution alleles of 8 classical HLA genes and SNP genotype data.6 Similarly, DEEP*HLA performed better than the other methods; and was more advantageous as alleles were low frequent or rare (Fig. 2a and Supplementary Table2).

Figure 2.
Figure 2. Performance evaluations of HLA imputation methods

(a-d) Sensitivity (upper) and specificity (lower) for the 4-digit alleles (a, b) and the amino acid polymorphisms (c, d) evaluated in our Japanese reference panel (a, c) and T1DGC reference panel (b, d). For each metrics, those for alleles of which frequency is less than a value on the horizontal axis are shown on the vertical axis. As a whole, DEEP*HLA outperformed other methods especially in specificity and imputing infrequent alleles. (e) Processing time (upper) and maximum memory usage (lower) evaluated on imputing the BBJ samples using the Japanese panel. DEEP*HLA imputed by far the fastest in total processing time as the sample size increased. All methods exhibited maximum memory usage scaling roughly linearly with sample size. SNP2HLA did not work within 100 GB in our machine for the sample size of more than 20,000.

Next, we applied DEEP*HLA to the Type 1 Diabetes Genetics Consortium (T1DGC) reference panel of 5,122 unrelated individuals of European ancestries.25 It consists of 2- and 4-digit alleles of the 8 classical HLA gene. DEEP*HLA achieved sensitivity and specificity of 0.976 in 4-digit resolution, which were superior to SNP2HLA (sensitivity of 0.972 and specificity of 0.935) and HIBAG (sensitivity and specificity of 0.959), was more advantageous as the alleles were low frequent or rare (Fig.2b and Supplementary Table 3). There were significant declines in the specificity of SNP2HLA especially for imputing infrequent alleles, because the sum of the allele dosages of each HLA gene of an individual can exceed the expected value (i.e. = 2.0) since it imputes each allele separately as a binary allele.

DEEP*HLA can define HLA amino acid polymorphisms without ambiguity

DEEP*HLA separately imputes classical alleles of each HLA gene, as a multi-label classification in the field of machine learning. Thus, it has an advantage that the sum of imputed allele dosages of each HLA gene is definitely set as an ideal value of 1.0 per a haplotype. This feature enables us to define a dosage of amino acid polymorphisms from the imputed 4-digit allele dosages without ambiguity. Then, we compared this method of imputing amino acid polymorphisms with SNP2HLA, which imputes them as binary alleles. Although DEEP*HLA was equivalent with SNP2HLA in both accuracy metrics in imputing amino acid polymorphisms in total (0.997 vs 0.997 in the Japanese panel; 0.996 vs 0.996 in T1DGC panel; Supplementary Table 4, 5), it achieved more accurate imputation for low-frequency and rare alleles (Fig. 2c, d). As well as in imputing classical HLA alleles, the performance improvement was remarkable in specificity evaluated in T1DGC data.

High performance of DEEP*HLA in computational costs

We benchmarked the computational costs of DEEP*HLA against SNP2HLA and HIBAG using subset of GWAS dataset from BBJ containing n = 1,000, 2,000, 5,000, 10,000, 20,000, 50,000, and 100,000 samples (2,000 SNPs consistent with the reference panel). Unlike SNP2HLA, DEEP*HLA and HIBAG require pre-phased GWAS data and the models trained with reference data. Thus, we compared the total processing time including pre-phasing of GWAS data, training the models, and imputation of DEEP*HLA and HIBAG, with the running time of SNP2HLA. We used a state-of-art GPU, GeForce RTX 2080 Ti in training DEEP*HLA. As shown in Fig. 2e, DEEP*HLA imputation was by far the fastest in total processing time as the sample size increased. When comparing the pure imputation times, it was faster than HIBAG (Supplementary Table 6). As for memory cost, all methods exhibited maximum memory usage scaling roughly linearly with sample size (Fig. 2e and Supplementary Table 6), and HIBAG was the most memory-efficient through all the sample sizes. While SNP2HLA did not work within 100 GB memory of our machine for the sample size of more than 20,000, DEEP*HLA was able to impute even the biobank-scale sample size that reached 100,000.

Characteristics of the alleles where DEEP*HLA was advantageous to impute

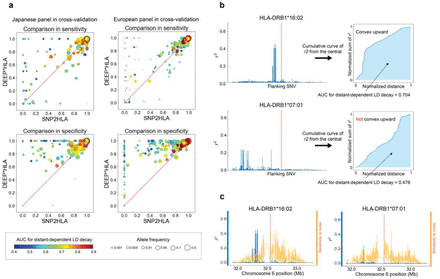
We focused on the characteristics of the HLA alleles of which accuracy was improved by our method in comparison with SNP2HLA, which was second to our method in total accuracy metrics. SNP2HLA runs Beagle intrinsically, which performs imputation based on hidden Markov model of a localized haplotype-cluster. We hypothesized that this kind of methods works better for imputing alleles of which LDs with the surrounding SNVs are stronger in close positions and get weaker as more distant from the target HLA allele (we termed this feature as distant-dependent LD decay). Conversely, it could be limited at imputing alleles which have sparse LD structures throughout the MHC region. To verify this hypothesis, we defined the area under curve (AUC) representing distant-dependent LD decay. The AUC values become higher when LDs with the surrounding SNVs get stronger as they get closer to the target HLA allele (Fig. 3b). We evaluated how much two accuracies of DEEP*HLA and SNP2HLA are affected by the AUC values and allele frequency with a multivariate linear regression analysis. As expected, both sensitivity and specificity were positively correlated with AUC in SNP2HLA. On the other hand, the specificity in DEEP*HLA were less dependent on AUC, and there was no significant correlation with the specificity in cross-validation on the Japanese panel (P = 0.069; Fig. 3a and Supplementary Table 7).

Figure 3.
Figure 3. Comparison between DEEP*HLA and SNP2HLA displayed with allele frequencies and AUC for distance-dependent LD decay

(a) Comparisons of imputation accuracy between DEEP*HLA and SNP2HLA in sensitivity (upper) and specificity (lower) for 4-digit allele imputation for cross-validation on the Japanese panel (left) and T1DGC panels (right). Each dot corresponds to one allele, displayed with allele frequencies (size) and AUC for distance-dependent LD decay (color). Those of which specificities were less than 0 are shown with converted to 0 for visibility. Performance of SNP2HLA was limited when imputing the alleles with low frequency and low AUC, DEEP*HLA was relatively accurate even for the less frequent alleles regardless of the AUC. (b) Example illustrations of AUC for distance-dependent LD decay. The left figures illustrate r2 of LD between an HLA allele (red dash line in the central) and flanking SNVs. HLA-DRB1*16:02 has strong LD in close positions and weaker in the distance; and cumulative curve of r2 of bilateral SNVs becomes convex upward; and the AUC becomes bigger. In contrast, HLA-DRB1*07:01 has moderate LD in distant or sparse positions; and the curve does not become convex upward; and the AUC becomes smaller. (c) Comparison between r2 (blue line) and sensitivity maps of DEEP*HLA (orange line) for example alleles (red dash line in the central). The sensitivities are normalized for visibility. In both examples, DEEP*HLA reacted to noises across an extensive area regardless of LD.

Next, to investigate our assumption that DEEP*HLA performs better imputation by recognizing distant SNVs as well as close SNVs of strong LD, we applied SmoothGrad, a method for generating a sensitivity map of a deep learning model.26 It is a simple approach based on the idea of adding noise to the input data and taking the average of the resulting sensitivity maps for each sampled data. As displayed in its application to example HLA alleles, a trained DEEP*HLA model reacted to the noises of not only the surrounding SNVs with strong LD, but also the distant SNVs (Fig. 3c). Interestingly, the strongly reacted SNVs were not always those of even moderate LD, but also spread across the entire the input region. While the validity of SmoothGrad for a deep learning model of genomic data has under investigation, one probable explanation is that predicting an allele by our method conversely means predicting absence of the other alleles of the target HLA gene; thus, any SNV positions in LD with any of the other HLA alleles could be informative. Another explanation is that DEEP*HLA might recognize complicated combinations of multiple distinct SNVs within the region, rather than the simple HLA allele-SNV LD correlations.

Empirical evaluation of imputation uncertainty in deep learning models

A common issue of deep learning models is how to quantify the reliability of their predictions; and one potential solution is uncertainty inferred from the idea of Bayesian deep learning.27 Then, we experimentally evaluated the uncertainty of imputation by DEEP*HLA using Monte Carlo (MC) dropout, which could be applied following general implementation of neural networks with dropout units.28,29 In MC dropout, uncertainty was presented as entropy of sampling variation with keeping dropout turned on. This uncertainty index corresponds not to each binary allele of a gene, but to the prediction of genotype of a gene of an individual. Thus, we evaluated whether it could guess the correctness of best-guess genotypes of the target HLA genes. We compared it with a dosage-based discrimination, in which we assume that a best-guess imputation of higher genotype dosage (probability) is more likely to be correct. The entropy-based uncertainty identified incorrectly imputed genotypes in areas under the curve of the receiver operating characteristic (ROC-AUC) of 0.851 in the Japanese panel, and of 0.883 in T1DGC reference panel in 4-digit alleles, which were superior to dosage-based discrimination (ROC-AUC = 0.722 in the Japanese panel and = 0.754 in T1DGC panel; Supplementary Fig. 1). Whereas the estimation of prediction uncertainty of a deep learning model is still developing;29 our results might illustrate its potential applicability to establishment of a reliability score for genotype imputation by deep neural networks.

Trans-ethnic MHC fine-mapping of T1D

We applied the DEEP*HLA models trained with the Japanese panel and T1DGC panel to HLA imputation of T1D GWAS data of BBJ (831 cases and 61,556 controls) and UKBB (732 cases and 356,123 controls), respectively. T1D is a highly heritable autoimmune disease that results from T cell-mediated destruction of insulin-producing pancreatic β cells.30 We separately imputed GWAS data of the cohorts and then combined them to perform trans-ethnic MHC fine-mapping (1,563 cases and 417,679 controls). Association analysis of the imputed HLA variants with T1D found the most significant association at the HLA-DRβ1 amino acid position 71 (Pomnibus = P = 6.2 × 10−119; Fig. 4a and Supplementary Table 8), one of the T1D risk amino acid polymorphisms in the European population.10 In T1D, the largest HLA gene associations were reported in the HLA-DRB1, -DQA1, and -DQB1;10,31 thus, we further investigated independently associated variants within these HLA genes. When conditioning on HLA-DRβ1 amino acid position 71, we observed the most significant independent association in HLA-DQβ1 amino acid position 185 (Pomnibus = 8.9 × 10−69). Through stepwise forward conditional analysis in the class II HLA region, we found significant independent associations in on Tyr30 in HLA-DQβ1 (Pbinary = 9.6 × 10−20), HLA-DRβ1 amino acid position 74 (Pomnibus = 14 × 10−11), and Arg70 in HLA-DQβ1 (Pomnibus = 4.5 × 10−9; Supplementary Fig.2 and Supplementary Table 9). The association of HLA-DRβ1 amino acid position 74 has been previously reported in Europeans.32

Figure 4.
Figure 4. Trans-ethnic association plots of the HLA variants with T1D in the MHC region.

Diamonds represent –log10 (P values) for the tested HLA variants, including SNPs, classical alleles and amino acid polymorphisms of the HLA genes. The dashed black horizontal lines represent the genome-wide significance threshold of P = 5.0×10−8. The physical positions of the HLA genes on chromosome 6 are shown at the bottom. (a-e) Each panel shows the association plot in the process of stepwise conditional regression analysis: nominal results. (a) Results conditioned on HLA-DRB1, HLA-DQA1, and HLA-DRB1. (b) Results conditioned on HLA-DRB1, HLA-DQA1, HLA-DRB1, and HLA-A. (c) Results conditioned on HLA-DRB1, HLA-DQA1, HLA-DRB1, HLA-A, and HLA-B. (d) Our study identified independent contribution of multiple HLA class I and class II genes to T1D risk in a trans-ethnic cohort, of which the impacts of class II HLA genes was more evident. Detailed association results are available in Supplementary Table 4.

These results were different from a previous study of large T1D cohort of European ancestries, which reported three amino acid polymorphisms at HLA-DQ 1 position 57, HLA-DRβ1 position 13, and HLA-DRβ1 position 71 were top-associated amino acid polymorphisms in the HLA-DRB1, -DQA1, and -DQB1 region. We then constructed multivariate regression models for individual population that incorporated our T1D risk-associated HLA amino acid polymorphisms and classical alleles of HLA-DRB1 and HLA-DQB1, and compared the effects of these variants. Whereas the odds ratios of the risk-associated variants reported previously did not show any positive correlation between different populations (Pearson’s r = -0.59, P = 0.058; Supplementary Fig.3 and Supplementary Table 10), those observed in our analyses presented significant positive correlation (Pearson’s r = 0.76, P = 6.8 × 10−3; Supplementary Fig.3).

We further investigated whether T1D risk was associated with other HLA genes independently of HLA-DRB1, -DQA1, and -DQB1. When conditioning on HLA-DRB1, -DQA1, and -DQB1, we identified a significant independent association at HLA-A amino acid position 62 (Pomnibus = 5.4 × 10; Fig. 4b and Supplementary Table 8). After conditioning on HLA-A amino acid position 62, we did not observe any additional independent association in HLA-A alleles. When we conditioned on HLA-DRB1, -DQA1, -DQB1, and -A, we identified a significant independent association at HLA-B*54:01 (Pbinary = 1.3 × 10−9; Fig. 4c and Supplementary Table 8), and its unique amino acid alleles (Gly45 and Val52 at HLA-B). HLA-B*54:01 has traditionally been suggested as a risk allele in Japanese by a candidate HLA gene approach.11 Its independent association through the MHC region-wide fine-mapping was first proven here. When conditioning on HLA-DRB1, -DQA1, -DQB1, -A, and -B, no variants in the MHC region satisfied the genome-wide significance threshold (P > 5.0 × 10−8; Fig. 4d and Supplementary Table 8). Multivariate regression analysis of the identified risk variants explained 10.3% and 27.6% of the phenotypic variance in T1D under assumption of disease prevalence of 0.014% and 0.4%34 for Japanese and British cohorts, respectively. Their odds ratios on T1D risk were also correlated between different populations (Pearson’s r = 0.71, P = 4.4 × 10−3; Table 1).

View this table:
Tables 1. Associations of the HLA variants with T1D risk identified through the trans-ethnic fine-mapping study.

Discussion

In this study, we demonstrated that DEEP*HLA, a multi-task convolutional deep learning method for HLA imputation, outperformed conventional HLA imputation methods both in sensitivity and specificity. DEEP*HLA was more advantageous when the target HLA variants, including classical alleles and amino acid polymorphisms, were low frequent or rare. Our study demonstrated that a conventional method dropped its performance for the alleles which did not exhibit distant-dependent LD decay features with the target HLA allele. DEEP*HLA was not restricted to this point, and comprehensively captures the relationships among distinct multiple variants regardless of LD.

To date, technical application of deep neural networks to population genetics data has been limited. In a previous attempt for genotype imputation, a sparse convolutional denoising autoencoder was only compared with reference-free methods.24 There might be two possible reasons for the success of our DEEP*HLA. First unlike genotype imputation by denoising autoencoders, which assumed various positions of missing genotypes in a reference panel to impute, the prediction targets were fixed to the HLA allele genotypes as a classification problem. Second, convolutional neural networks, which leverage a convolutional kernel that is capable of learning various local patterns, might be suited for learning the complicated LD structures of the MHC region.

We filtered alleles of poor imputation quality based on the results of cross-validation in the current application; however, an indicator of reliability could be further utilized. We demonstrated that the uncertainty of prediction inferred from a Bayesian deep learning method had potential capability of distinguishing incorrectly-imputed alleles in per-gene of individuals. Our future work should establish a method to quantify per-allele uncertainty of imputation which could be practically used as a filtering threshold for subsequent analyses.

Taking advantage of the significant improvement of imputation accuracy for rare alleles, we conducted trans-ethnic MHC fine-mapping in T1D. Our study successfully disentangled a set of independently associated amino acid polymorphisms and HLA alleles. This approach could be performed as well using the conventional HLA imputation methods. However, the results obtained by our method should be more reliable since there were several risk-associated alleles which were rare only in one population. As a result, the catalogue of the T1D risk-associated variants by our trans-ethnic approach were different from those of the previous study in Europeans.10 We admit the possibility that the smaller sample size in our study and different definition of the phenotypes (between studies, and between cohorts in our study) might also contribute to this disparity. Especially, we note potential distinctiveness of Japanese T1D phenotypes.35 Considering that our observed variants shared the effects on the T1D risk between different populations, however, we might gain a novel insight into the issue of inter-ethnic heterogeneity of T1D risk allele in the MHC region.

In terms of trans-ethnic analysis, we targeted the two major populations of Europeans and east Asians. As a next step, multi-ethnic MHC fine-mapping integrating further diverse ancestry should be warranted for robust prioritization of risk-associated HLA variants.13 Given their high learning capacity of deep neural networks, our method should be helpful not only when integrating the imputation results of multiple references, but also when using a more comprehensive multi-ethnic reference. We expect that highly accurate imputation realized by learning of complex LDs in the MHC region using neural networks will enable us to further elucidate the involvement of common genetic features in the MHC region that affect complex traits beyond ethnicity.

Data Availability

The Japanese HLA data have been deposited at the National Bioscience Database Center (NBDC) Human Database (research ID: hum0114). Independent HLA genotype data of Japanese population is available in the Japanese Genotype-phenotype archive (JGA; accession ID: JGAS00000000018). T1DGC HLA reference panel can be download at a NIDDK central repository with a request (https://repository.niddk.nih.gov/studies/t1dgc-special/). GWAS data of the BBJ are available at the NBDC Human Database (research ID: hum0014). UKBB GWAS data is available upon request (https://www.ukbiobank.ac.uk/).

Conflicts of interests

The authors declare no conflicts of interests.

Data availability

The Japanese HLA data have been deposited at the National Bioscience Database Center (NBDC) Human Database (research ID: hum0114). Independent HLA genotype data of Japanese population is available in the Japanese Genotype-phenotype archive (JGA; accession ID: JGAS00000000018). T1DGC HLA reference panel can be download at a NIDDK central repository with a request (https://repository.niddk.nih.gov/studies/t1dgc-special/). GWAS data of the BBJ are available at the NBDC Human Database (research ID: hum0014). UKBB GWAS data is available upon request (https://www.ukbiobank.ac.uk/).

Code availability

Python scripts for training a model and performing imputation with our method are in DEEP*HLA GitHub repository (https://github.com/tatsuhikonaito/DEEP-HLA).

Methods

The architecture of DEEP*HLA

DEEP*HLA is a multitask convolutional neural network with a shared part of two convolutional layers and a fully-connected layer, and individual fully-connected layers which output allelic dosages of individual HLA genes to impute simultaneously HLA genes of the same group (Supplementary Fig.4). The grouping was based on the LD structure3 and physical distance in the current application: (1) {HLA-F, HLA-V, HLA-G, HLA-H, HLA-K, HLA-A, HLA-J, HLA-L, HLA-E}, (2) {HLA-C, HLA-B, MICA, MICB}, (3) {HLA-DRA, HLA-DRB9, HLA-DRB5, HLA-DRB4, HLA-DRB3, HLA-DRB8, HLA-DRB7, HLA-DRB6, HLA-DRB2, HLA-DRB1, HLA-DQA1, HLA-DOB, HLA-DQB1}, and (4) {TAP2, TAP1, HLA-DMB, HLA-DMA, HLA-DOA, HLA-DPA1, HLA-DPB1}. Genes which were not typed or had only one allele in individual reference panels were excluded from the group.

For each group, SNPs within its window are encoded to one-hot vectors based on whether each genotype is consistent with a reference or alternative allele. The window sizes on each side were set to 500 kb in the current investigation. Two convolutional layers with max-pooling layers and a fully-connected layer follow the input layer as a shared part. The fully-connected layer in the end of shared part is followed by each fully-connected layer which has nodes consistent with the number of alleles of each HLA gene. To return a dosage of imputation, which ranges from 0.0 to 1.0 for a haplotype, softmax activation was added before the last output. Dropout was used on the convolutional and fully-connected layers,36 and batch normalization was added to the convolutional layers.37

During training, 5% of data set were spared for validation to determine the point for early-stopping training (i.e. we used 85% of data were used for training in 10-fold cross-validation). Categorical cross entropy loss function of each HLA gene was minimized using the Adam optimizing algorithm.38 As a multi-task learning to find a Pareto optimal solution of all tasks, we used the multiple-gradient descent algorithm – upper bound (MGDA-UB), where the loss function of each task is scaled based on its optimization algorithms.39 To taking advantage of the hierarchical nature of HLA alleles (i.e. 2-digit, 4-digit, and 6-digit), we implemented hierarchical fine-tuning, in which the parameters of model of upper hierarchical structures were transferred to those of the lower one.40 We transferred the parameters of shared networks of 2-digit alleles to 4-digit alleles, and of 4-digit alleles to 6-digit alleles during training successively. Although some HLA alleles in our reference panel were not determined in 4-digit or 6-digit resolution, we set their upper resolution instead to keep equivalent hierarchical levels with other HLA genes. Hyperparameters, including the number of filters and kernel sizes of convolutional layers, fully-connected layer size, were tuned with Optuna.41 The hyperparameters of the Japanese model were determined using an randomly sampled set before cross-validation, and the same values were used for hyper-parameters of the European model. Our deep learning architectures were implemented using Pytorch 1.4.1 (see URLs), a Python neural network library.

Empirical evaluation of HLA imputation accuracy

We defined two metrics to evaluate the imputation accuracy of the gene-level dosage in various aspects. First, the accuracy was calculated by summing across all individuals the dosage of each true allele in the individual, and divided by the total number of observation, as proposed in the paper of SNP2HLA.25 We defined this as sensitivity Se because it counts positives that are correctly identified as such. 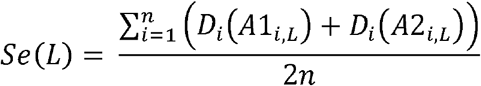Embedded Image where n denotes the number of individuals, Di represents the imputed dosage of an allele in individual i, and alleles A1i, L and A2i, L represent the true HLA alleles for individual i at locus L. In contrast, we defined specificity Sp as

Embedded Image

where alleles 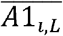Embedded Image and Embedded Image represent the HLA alleles which are incorrectly imputed dosage for individual i at locus L. Due to the nature of formula, total sensitivity and specificity of each HLA gene should be the same value for DEEP*HLA and HIBAG, in which the sum of dosage in each HLA gene of each individual is constant.

We extended these metrics for each gene to evaluate imputation performance of each allele A. Embedded Image where m denotes the number of true observations of allele A in total sample, and Di represents imputed dosage of allele A in individual haplotype j which has allele A. Dk represents imputed dosage of allele A in individual haplotype k of which true allele is not A (note, Sp(A) can be a negative value). Although these metrics are different from their general definitions, they are adjusted for bias due to allele frequency by dividing by true number of alleles.

When averaging the accuracy metrics, we weighted them by allele frequency.

Estimation of HLA imputation uncertainty of DEEP*HLA using MC dropout method

In order to provide uncertainty of prediction, we adopted the entropy of sampling variation of MC dropout method.28 In MC dropout, dropout are kept during prediction to perform multiple model calls. Different units are dropped across different model calls; thus, it can be considered as Bayesian sampling with treating the parameters of a CNN model as random variables of Bernoulli distribution. The uncertainty of a best-guess genotype inferred from the entropy of sampling variation is determined as Embedded Image where T is the number of variational samplings and t is the number of times in which obtained genotype was same as the best-guess genotype. We set T = 200 in the current investigation.

AUC metric representing distant-dependent LD decay

To evaluate whether the LD between an HLA allele and its surrounding SNVs gets weaker as the SNVs are distant to it, we calculated the area under the curve (AUC) of the cumulative curve of r2 from the HLA allele (AUC for distance-dependent LD decay). When the LD of flanking SNVs of an HLA allele has such a characteristic, r2 measure of LD tends to decline from the HLA allele. In other words, the bilateral cumulative curve of r2 from the HLA allele should be more likely to be convex upward; then the AUC tends to be higher. We determined the AUC by normalizing the maximum values of r2 sum and window sizes to 1. We evaluated its association with accuracies of each imputation method by linear regression model adjusted with an allele frequency and the maximum value of r2. We set window size as the range of its input for evaluating the association with DEEP*HLA, and 1,000 for SNP2HLA.

Regional sensitivity maps of DEEP*HLA

We applied SmoothGrad approach to estimate which SNVs were important for DEEP*HLA to impute genotypes of each HLA gene.26 For each haplotype, we generated 200 samples which were added Gaussian noise to encoded SNV data and input them to a trained model, and obtained the sensitivity values for individual SNV positions by averaging the absolute values of gradients caused by the difference from the true label. When we obtained the sensitivity of an allele, we averaged the maps of all haplotypes which truly has the allele.

HLA imputation software and parameter settings

We tested the latest version of each software available in Jun 2020 to compare with our method. SNP2HLA (v1.0.3) first arranges the strand in its own algorithm; however, we removed this step data during cross-validation, in which the strands must be the same between training and test data. Other settings of SNP2HLA were set to the default values. HIBAG (1.22.0.) receives phased genotypes data as input; and we used phased data generated using Beagle as well as our method. The number of classifiers were set to 25, which is sufficient to provide good performance,42 in testing with the Japanese. For T1DGC panel, training time was extremely long with 25 classifiers; thus, we set 2 of classifiers after we confirmed that the imputation accuracy was almost unchanged in the first set of cross-validation. Flanking regions on each side was set to 500 kb.

Computational costs measurement

We measured the computational costs of imputation of subset of BioBank Japan (BBJ) Project data set (n = 1,000, 2,000, 5,000, 10,000, 20,000, 50,000, and 100,000 samples) by our Japanese reference panel (2,000 SNVs were consistent). All our runtime analyses except model training of DEEP*HLA were performed on a dedicated server running CentOS 7.2.1511, with 48 CPU cores (Intel ® Xeon ® E5-2687W v4 @ 3.00 GHz) and 256 GB of RAM without GPU. The model training of DEEP*HLA was conducted on Ubuntu 16.04.6 LTS with 20 CPU cores (Intel ® Core ™ i9-9900X @ 3.50 GHz), 2 GPUs (NVIDIA ® GeForce ® RTX 2080 Ti), and 128 GB of RAM. DEEP*HLA and HIBAG require pre-phased GWAS data and the models trained with reference data; thus, we measured the process not only of imputation, but also of pre-phasing of GWAS data (conducted by Eagle) and training the models with a reference panel. In SNP2HLA, the maximum of available memory was set to 100 GB. The processing time and maximum memory usage was measured using GNU Time software when running from a command line interface.

HLA imputation reference data

(i) Our Japanese reference panel and a validation dataset

Our Japanese reference panel contains NGS-based 6-digit resolution HLA typing data of 33 classical and non-classical HLA genes, of which 9 were classical HLA genes (HLA-A, HLA-B, and HLA-C for class I; HLA-DRA, HLA-DRB1, HLA-DQA1, HLA-DQB1, HLA-DPA1, and HLA-DPB1 for class II) and 24 were nonclassical HLA genes (HLA-E, HLA-F, HLA-G, HLA-H, HLA-J, HLA-K, HLA-L, HLA-V, HLA-DRB2, HLA-DRB3, HLA-DRB4, HLA-DRB5, HLA-DRB6, HLA-DRB7, HLA-DRB8, HLA-DRB9, HLA-DOA, HLA-DOB, HLA-DMA, HLA-DMB, MICA, MICB, TAP1, and TAP2), along with high-density SNP data of the MHC region by genotyping with the Illumina HumanCoreExome BeadChip (v1.1; Illumina) of 1,120 unrelated individuals of Japanese ancestry.3 Among them, we excluded 2 individuals’ data in which sides of some HLA alleles were inconsistent among different resolutions after pre-phasing.

To benchmark the imputation performance when the Japanese panel is applied to independent dataset, we used 908 individuals of Japanese ancestries with 4-digit resolution alleles of classical HLA genes (HLA-A, HLA-B, HLA-C, HLA-DRB1, HLA-DQA1, HLA-DQB1, HLA-DPA1), which was used as a HLA reference panel in our previous study.6 It contains high-density SNP data genotyped with four SNP genotyping arrays (the Illumina HumanOmniExpress BeadChip, the Illumina HumanExome BeadChip, the Illumina Immunochip, and the Illumina HumanHap550v3 Genotyping BeadChip). This study was approved by the ethical committee of Osaka University Graduate School of Medicine.

(ii) The Type 1 Diabetes Genetics Consortium (T1DGC) reference panel

T1DGC panel contains 5,868 SNPs (genotyped with Illumina Immunochip) and 4-digit resolution HLA typing data of classical HLA genes (HLA-A, HLA-B, and HLA-C for class I, HLA-DPA1, HLA-DPB1, HLA-DQA1, HLA-DQB1, and HLA-DRB1 for class II) of 5,225 unrelated individuals of European ancestries.14 Among them, we excluded 103 individuals’ data in which sides of some HLA alleles were inconsistent among different resolutions after pre-phasing.

T1D GWAS data in the Japanese population

The BioBank Japan (BBJ) is a multi-institutional hospital-based registry that comprised DNA, serum, and clinical information of approximately 200,000 individuals of Japanese ancestry in 2003-2007.43,44 We used GWAS data from 831 cases who had record of T1D diagnosis and 61,556 controls of Japanese genetic ancestry enrolled in BBJ Project. The controls were included in those enrolled in our previous study that investigated the association of the MHC region to comprehensive phenotypes, and the number of T1D cases was increased.3 The process of patient registration, the GWAS data, and the QC process have been described elsewhere.43–45

T1D GWAS data in the British population

The UK Biobank (UKBB) comprises health related information approximately 500,000 individuals aged between 40-69 who were recruited from across the United Kingdom in 2006-2010.46 We used GWAS data from 732 T1D patients and 356,123 controls of British genetic ancestry enrolled in UKBB. We selected T1D patients as individuals who were diagnosed as insulin-dependent diabetes mellitus in hospital records, and neither as non-insulin-independent diabetes mellitus in hospital records nor as type 2 diabetes in self-reported diagnosis. The controls were selected as individuals who did not have record of any autoimmune diseases neither in hospital records nor in self-reported diagnosis. We included only individuals of British ancestry according to self-identification and criteria based on principal component (PC).47 We excluded individuals of ambiguous sex (sex chromosome aneuploidy and inconsistency between self-reported and genetic sex), and outlier of heterozygosity or call rate of high quality markers.

Imputation of the HLA variants of GWAS data of T1D and control individuals

In this study, we defined the HLA variants as SNVs in the MHC region, classical 2-digit and 4-digit biallelic HLA alleles, biallelic HLA amino acid polymorphisms corresponding to the respective residues, and multi-allelic HLA amino acid polymorphisms for each amino acid position. We applied DEEP*HLA to the GWAS data to determine classical 2-digit and 4-digit biallelic HLA alleles. The dosages of biallelic HLA amino acid polymorphisms corresponding to the respective residues and multiallelic HLA amino acid polymorphisms for each amino acid position were determined from the imputed 4-digit classical allele dosages. We applied post-imputation filtering as the biallelic alleles of which both the sensitivity and specificity in 10-fold cross-validation were higher than 0.7. The sensitivity and specificity of the current definition could be overestimated if an allele frequency is above 0.5; thus, we calculated those with allele reversed (i.e. flipping reference/alternative alleles) and filtered also by them. The SNVs in the MHC region were imputed using minimac3 (version 2.0.1) after pre-phased with Eagle (version 2.3). We applied stringent post-imputation QC filtering of the variants (minor allele frequency ≥ 0.5% and imputation score Rsq ≥ 0.7). For trans-ethnic fine-mapping, we integrated the results of imputation of individual cohorts by including the HLA genes, amino acid position, and SNVs which were typed in both reference panels. Regarding the HLA alleles and amino acid polymorphisms that existed in one population, they were regarded as absent on the other population. Considering the disparity in allele frequency of SNVs among different populations, we removed all palindromic SNVs to align the strands correctly without fail.

Association testing of the HLA variants

We assumed additive effects of the allele dosages on the log-odds scale for susceptibility of T1D; and evaluated associations of the HLA variants with the risk of T1D using a logistic regression model. To robustly account for potential population stratification, we included the top ten PCs obtained from the GWAS genotype data of each cohort (not including the MHC region) as covariates in the regression model. For trans-ethnic analysis, PC terms of each other population were set to 0; and, besides, we added a categorical variable indicating a population as a covariate. We also included sex of individuals as a covariate.

To evaluate independent risk among the HLA variants and genes, we conducted a forward-type stepwise conditional regression analysis that additionally included the binary HLA variant genotypes as covariates. When conditioned on HLA gene(s), we included all the 4-digit alleles as covariates to robustly condition the associations attributable to the HLA genes, as previously described.3,12 When conditioning on the specific HLA amino acid position(s), we included the multi-allelic variants of the amino acid residues. We applied a forward stepwise conditional analysis for the HLA variants and then HLA genes, based on the genome-wide association significance threshold (P = 5.0 × 10−8).

We tested a multivariate full regression model by including the risk-associated HLA variants in HLA-DRB1, HLA-DQB1, HLA-A, and HLA-B, which were identified through the stepwise regression analysis. When we included amino acid polymorphisms in the model, we excluded the most frequent residue in the British cohort from each amino acid position as the reference allele. The phenotypic variance explained by the identified risk-associated HLA variants was estimated on the basis of a liability threshold model assuming the population-specific prevalence of T1D and using the effect sizes obtained from the multivariate regression model.

Acknowledgements

We would like to thank all the participants involvement in this study. We thank the members of Biobank Japan and RIKEN Center for Integrative Medical Sciences for their supports on this study.

References

  1. 1.↵
    Dendrou, C. A., Petersen, J., Rossjohn, J. & Fugger, L. HLA variation and disease. Nat. Rev. Immunol. 18, 325–339 (2018).
    OpenUrlCrossRefPubMed
  2. 2.↵
    Erlich, H. HLA DNA typing: Past, present, and future. Tissue Antigens 80, 1–11 (2012).
    OpenUrlCrossRefPubMedWeb of Science
  3. 3.↵
    Hirata, J. et al. Genetic and phenotypic landscape of the major histocompatibilty complex region in the Japanese population. Nat. Genet. 51, 470–480 (2019).
    OpenUrlCrossRefPubMed
  4. 4.
    International HIV Controllers Study et al. The major genetic determinants of HIV-1 control affect HLA class I peptide presentation. Science 330, 1551–1557 (2010).
    OpenUrlAbstract/FREE Full Text
  5. 5.
    Raychaudhuri, S. et al. Five amino acids in three HLA proteins explain most of the association between MHC and seropositive rheumatoid arthritis. Nat. Genet. 44, 291–296 (2012).
    OpenUrlCrossRefPubMed
  6. 6.↵
    Okada, Y. et al. Construction of a population-specific HLA imputation reference panel and its application to Graves’ disease risk in Japanese. Nat. Genet. 47, 798–802 (2015).
    OpenUrlCrossRefPubMed
  7. 7.↵
    Gourraud, P. A. et al. HLA diversity in the 1000 genomes dataset. PLoS One 9, (2014).
  8. 8.↵
    Okada, Y. et al. Risk for ACPA-positive rheumatoid arthritis is driven by shared HLA amino acid polymorphisms in Asian and European populations. Hum. Mol. Genet. 23, 6916–6926 (2014).
    OpenUrlCrossRefPubMed
  9. 9.↵
    Todd JA, Bell JI & McDevitt HO. HLA-DQbeta gene contributes to susceptibility and resistance to insulin-dependent diabetes mellitus. Nature 329, 599–604 (1987).
    OpenUrlCrossRefPubMedWeb of Science
  10. 10.↵
    Hu, X. et al. Additive and interaction effects at three amino acid positions in HLA-DQ and HLA-DR molecules drive type 1 diabetes risk. Nat. Genet. 47, 898–905 (2015).
    OpenUrlCrossRefPubMed
  11. 11.↵
    Kawabata, Y. et al. Differential association of HLA with three subtypes of type 1 diabetes: Fulminant, slowly progressive and acute-onset. Diabetologia 52, 2513–2521 (2009).
    OpenUrl
  12. 12.↵
    Okada, Y. et al. Contribution of a Non-classical HLA Gene, HLA-DOA, to the Risk of Rheumatoid Arthritis. Am. J. Hum. Genet. 99, 366–374 (2016).
    OpenUrlPubMed
  13. 13.↵
    Luo, Y. et al. A high-resolution HLA reference panel capturing global population diversity enables multi-ethnic fine-mapping in HIV host response. Preprint at https://www.medrxiv.org/content/10.1101/2020.07.16.20155606v1 (2020).
  14. 14.↵
    Jia, X. et al. Imputing Amino Acid Polymorphisms in Human Leukocyte Antigens. PLoS One 8, (2013).
  15. 15.↵
    Levin, A. M. et al. Performance of HLA allele prediction methods in African Americans for class II genes HLA-DRB1, -DQB1, and -DPB1. BMC Genet. 15, 1–11 (2014).
    OpenUrlPubMed
  16. 16.↵
    Karnes, J. H. et al. Comparison of HLA allelic imputation programs. PLoS One 12, 1–12 (2017).
    OpenUrlCrossRefPubMed
  17. 17.↵
    Eraslan, G., Avsec, Ž., Gagneur, J. & Theis, F. J. Deep learning: new computational modelling techniques for genomics. Nat. Rev. Genet. 20, 389–403 (2019).
    OpenUrlCrossRef
  18. 18.↵
    Alipanahi, B., Delong, A., Weirauch, M. T. & Frey, B. J. Predicting the sequence specificities of DNA- and RNA-binding proteins by deep learning. Nat Biotechnol 33, 831–838 (2015).
    OpenUrlCrossRefPubMed
  19. 19.
    Zhou, J. et al. Deep learning sequence-based ab initio prediction of variant effects on expression and disease risk. Nat. Genet. 50, 1171–1179 (2018).
    OpenUrlCrossRef
  20. 20.
    Sundaram, L. et al. Predicting the clinical impact of human mutation with deep neural networks. Nat. Genet. 50, 1161–1170 (2018).
    OpenUrlPubMed
  21. 21.↵
    Naito, T. Predicting the impact of single nucleotide variants on splicing via sequence-based deep neural networks and genomic features. Hum. Mutat. 40, 1261–1269 (2019).
    OpenUrl
  22. 22.↵
    Riesselman, A. J., Ingraham, J. B. & Marks, D. S. Deep generative models of genetic variation capture the effects of mutations. Nat. Methods 15, 816–822 (2018).
    OpenUrl
  23. 23.↵
    Dwivedi, S. K., Tjärnberg, A., Tegnér, J. & Gustafsson, M. Deriving disease modules from the compressed transcriptional space embedded in a deep autoencoder. Nat. Commun. 11, (2020).
  24. 24.↵
    Chen, J. & Shi, X. Sparse convolutional denoising autoencoders for genotype imputation. Genes (Basel). 10, 1–16 (2019).
    OpenUrl
  25. 25.↵
    Han, B. et al. Fine mapping seronegative and seropositive rheumatoid arthritis to shared and distinct HLA alleles by adjusting for the effects of heterogeneity. Am. J. Hum. Genet. 94, 522–532 (2014).
    OpenUrlCrossRefPubMed
  26. 26.↵
    Smilkov, D., Thorat, N., Kim, B., Viégas, F. & Wattenberg, M. SmoothGrad: removing noise by adding noise. Preprint at https://arxiv.org/abs/1706.03825 (2017).
  27. 27.↵
    Kendall, A. & Gal, Y. What uncertainties do we need in Bayesian deep learning for computer vision? Adv. Neural Inf. Process. Syst. 2017-Decem, 5575–5585 (2017).
  28. 28.↵
    Gal, Y. & Ghahramani, Z. Bayesian Convolutional Neural Networks with Bernoulli Approximate Variational Inference. Preprint at https://arxiv.org/abs/1506.02158 (2015).
  29. 29.↵
    Gal, Y. & Ghahramani, Z. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning. 33rd Int. Conf. Mach. Learn. ICML 2016 3, 1651–1660 (2016).
    OpenUrl
  30. 30.↵
    Atkinson, M. A., Eisenbarth, G. S. & Michels, A. W. Type 1 diabetes. Lancet 383, 69–82 (2014).
    OpenUrlCrossRefPubMedWeb of Science
  31. 31.↵
    Erlich, H. et al. HLA DR-DQ haplotypes and genotypes and type 1 diabetes risk analysis of the type 1 diabetes genetics consortium families. Diabetes 57, 1084–1092 (2008).
    OpenUrlAbstract/FREE Full Text
  32. 32.↵
    Cucca, F. A correlation between the relative predisposition of MHC class II alleles to type 1 diabetes and the structure of their proteins. Hum. Mol. Genet. 10, 2025–2037 (2001).
    OpenUrlCrossRefPubMedWeb of Science
  33. 33.
    Onda, Y. et al. Incidence and prevalence of childhood-onset Type 1 diabetes in Japan: the T1D study. Diabet. Med. 34, 909–915 (2017).
    OpenUrlPubMed
  34. 34.↵
    Sivertsen, B., Petrie, K. J., Wilhelmsen-Langeland, A. & Hysing, M. Mental health in adolescents with Type 1 diabetes: Results from a large population-based study. BMC Endocr. Disord. 14, 1–8 (2014).
    OpenUrlCrossRefPubMed
  35. 35.↵
    Kawasaki, E. & Eguchi, K. Is type 1 diabetes in the Japanese population the same as among Caucasians? Ann. N.Y. Acad. Sci. 1037, 96–103 (2004).
    OpenUrlCrossRefPubMed
  36. 36.↵
    Srivastava, N., Hinton, G. E., Krizhevsky, A., Sutskever, I. & Salakhutdinov, R. DropoutL: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 15, 1929–1958 (2014).
    OpenUrlCrossRef
  37. 37.↵
    Ioffe, S. & Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. Proc. ICML 448–456 (2015).
  38. 38.↵
    Kingma, D. & Ba, J. Adam: A method for stochastic optimization. Int. Conf. Learn. Represent. (2015).
  39. 39.↵
    Sener, O. & Koltun, V. Multi-task learning as multi-objective optimization. Adv. Neural Inf. Process. Syst. 2018-Decem, 527–538 (2018).
  40. 40.↵
    Shimura, K., Li, J. & Fukumoto, F. HFT-CNN: Learning Hierarchical Category Structure for Multi-label Short Text Categorization. 811–816 (2019) doi:10.18653/v1/d18-1093.
    OpenUrlCrossRef
  41. 41.↵
    Akiba, T., Sano, S., Yanase, T., Ohta, T. & Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. Proc. ACM SIGKDD Int. Conf. Knowl. Discov. Data Min. 2623–2631 (2019).
  42. 42.↵
    Zheng, X. et al. HIBAG - HLA genotype imputation with attribute bagging. Pharmacogenomics J. 14, 192–200 (2014).
    OpenUrlCrossRefPubMed
  43. 43.↵
    Nagai, A. et al. Overview of the BioBank Japan Project: Study design and profile. J. Epidemiol. 27, S2–S8 (2017).
    OpenUrlCrossRefPubMed
  44. 44.↵
    Hirata, M. et al. Cross-sectional analysis of BioBank Japan clinical data: A large cohort of 200,000 patients with 47 common diseases. J. Epidemiol. 27, S9–S21 (2017).
    OpenUrlCrossRefPubMed
  45. 45.↵
    Kanai, M. et al. Genetic analysis of quantitative traits in the Japanese population links cell types to complex human diseases. Nat. Genet. 50, 390–400 (2018).
    OpenUrlCrossRefPubMed
  46. 46.↵
    Sudlow, C. et al. UK Biobank: An Open Access Resource for Identifying the Causes of a Wide Range of Complex Diseases of Middle and Old Age. PLoS Med. 12, 1–10 (2015).
    OpenUrlCrossRefPubMed
  47. 47.↵
    Bycroft, C. et al. The UK Biobank resource with deep phenotyping and genomic data. Nature 562, 203–209 (2018).
    OpenUrlCrossRefPubMed
Back to top
Posted August 13, 2020.
Download PDF
Data/Code
Email
A multi-task convolutional deep learning method for HLA allelic imputation and its application to trans-ethnic MHC fine-mapping of type 1 diabetes
Tatsuhiko Naito, Ken Suzuki, Jun Hirata, Yoichiro Kamatani, Koichi Matsuda, Tatsushi Toda, Yukinori Okada
medRxiv 2020.08.10.20170522; doi: https://doi.org/10.1101/2020.08.10.20170522
Twitter logo Facebook logo LinkedIn logo Mendeley logo
Citation Tools

Subject Area