Abstract
Background Pooling is a popular strategy for increasing SARS-CoV-2 testing throughput. A common pooling scheme is Dorfman pooling: test N individuals simultaneously. If the first test is positive — retest each individual.
Methods Using a probabilistic model, we analyze the false-negative rate (.i.e. the probability of a negative result for an infected individual) of Dorfman pooling. Our model is conservative in that it ignores sample dilution effects, which can only worsen pooling performance.
Results We show that one can expect a 60-80% increase in false-negative rates under Dorfman pooling, for reasonable parameter values. On average, when separate testing misses, e.g., ten infected individuals — Dorfman pooling misses more than sixteen.
Discussion In most pooling schemes, identifying an infected individual requires positive results in multiple tests and hence substantially increases false-negative rates. It is an inherent shortcoming of pooling schemes and should be kept in mind by policy makers.
1 Introduction
RT-PCR testing is a key component in breaking transmission chains and mitigating the COVID-19 pandemic. As such, the need for large-scale testing has resulted in development of pooling schemes of RT-PCR tests [1, 3, 4, 6, 7]. One such popular scheme is Dorfman pooling [1, 2]: Select N individuals and perform a single RT-PCR test on their combined (“pooled”) samples. If the pooled test yields a positive result — test each individual separately. The throughput efficiency of Dorfman pooling has been demonstrated empirically [1]. However, when test error rates are taken into consideration, a sharp increase in false-negative rates can be expected.
It is important to distinguish three types of false-negative events when performing pooling. For convenience, we follow a single infected individual, hence-forth referred to as “Donald”. A single test’s false-negative is the event of a negative result upon testing Donald separately, i.e., in a RT-PCR test without pooling. The probability of such an event is denoted Pfn. A pooled false-negative occurs when a pooled test containing Donald’s sample (and other samples) yields a negative result, i.e., the pooling fails to detect at least one positive result. Lastly, a scheme false-negative results occurs when an entire pooling scheme fails to identify Donald as infected. Our goal is to calculate Dorfman’s scheme false-negative rate. Or: what is the probability of Dorfman pooling not identifying Donald as infected?
2 Methods
2.1 Probabilistic Assumptions
We assume two pathways for a positive pooled test result: Viral RNA from an infected individual is correctly amplified; or, some testing error occurs, which causes an erroneous amplification. We ignore cross-reactivity with other Coronaviruses, which is negligible [10]. We assume a homogeneous and disconnected population (each individual is infected independently and with equal probability). For simplicity, we do not take into account sample dilution, since it can only further increase false-negative rates [1].
2.2 A simplistic approximation
For Dorfman’s scheme to yield a false-negative result, Donald has to test negative in either the single or the pooled test. If the infection prevalence is low, it is likely that Donald is the only infected individual in the pool. In this case, the false-negative probability of a pooled test equals the single test false-negative rate. See Section 2.3 for a precise calculation. The probability that Donald tests positive in both single and pooled test is then (1 −Pfn)2. Hence, the entire scheme’s false-negative rate is approximately the complement — 1 − (1 −Pfn)2.
2.3 Calculation of Dorfman’s scheme false-negative rate
Denote the prevalence of infection in the (tested) population q. As before, Pfn denotes the single RT-PCR test’s false-negative rate. We also denote Pfp the probability of introducing contaminated RNA in the pooling process (which may cause a false-positive). By our assumptions, a pool containing Donald’s sample and N − 1 other samples will yield a negative result if all of the following occur:
No contaminant RNA is introduced into the pooled samples. A false-positive does not occur, with probability 1 − Pfp.
The amplification process fails for Donald’s sample. A false-negative occurs, with probability Pfn.
The amplification process fails for the other N− 1 samples. For a single sample, the probability of being amplified is the prevalence of SARS-CoV-2 in the tested population q, multiplied by the true-positive rate. But the true-positive rate is the complement of Pfn, namely 1 − Pfn, hence the probability of amplification is q(1 − Pfn). For N − 1 such samples, the probability of not being amplified is (1 − q(1 − Pfn))N−1.
The pooled false-negative probability for Donald is simply the product of the terms above. Hence:
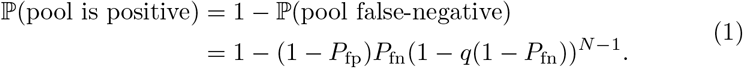
If the pooled test yields a positive result, Donald is tested separately. We assume such a simple procedure poses no risk of introducing contaminant RNA. Therefore, the separate test yields a positive result with probability 1− Pfn.
We calculate the probability that Donald is mistakenly identified as not infected — the scheme’s false-negative rate — denoted Psfn below. To correctly identify Donald as infected, both pooled and separate tests have to yield a positive result. Thus, the scheme’s false-negative rate Psfn is the complement of the product of the two previous terms:

2.4 Comparison metric
The single test false-negative Pfn and scheme false-negative rate Psfn are compared via:

Erel is the percentage increase in the pooling scheme false-negative rate, relative to the single test false-negative rate.
3 Results
To get a sense of the scheme’s false-negative rate, we first plug in Pfn = 0.2 [5,8–12] for the single test’s false-negative rate in the simplistic approximation of Section 2.2. We get that Dorfman’s scheme false-negative rate is approximately 1−(1−0.2)2 = 0.36. This figure, compared to the single test’s false-negative rate Pfn, amounts to Erel = 80%. Such an increase is an inevitable consequence of the fact that, for Donald to be identified as infected, he needs to test positively in two tests.
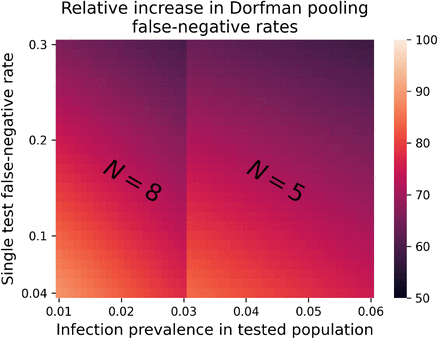
For the precise calculation, let us set false-negative and false-positive rates of Pfn = 0.2 [9–11] and Pfp = 0.05 [1, 12] along with a prevalence (among the tested) of q = 0.01 and a pool size of N = 8 [1]. In this case the scheme’s false-negative rate is Psfn = 0.34 and — a Erel = 70% increase compared to Pfn = 0.2, the assumed test’s false-negative rate. Other combinations of values can be found in Figure 1.
Relative increase in Dorfman pooling false-negative rates Erel. Color represents the relative percentage increase in the scheme false-negative rates relative to the single test false-negative rates, Pfn. The disease prevalence, q, is varied on the x-axis, while the single test false-negative rate is varied on the y-axis. Note that Pool size, N, was chosen according to q as in [1].
4 Discussion
Although pooling improves testing throughput, we have shown that it can potentially increase false-negative rates. This result remains qualitatively similar under varying parameter values, in the observed ranges (refs) (Figure 1). The calculation in the beginning of Section 3, although simplistic in nature, does capture the crux of the matter: In every step there is some probability of a false-negative result, and these probabilities accumulate.
Although we have shown the inherent risk of Dorfman pooling, this short-coming applies to other pooling schemes. Pooling schemes (e.g. [3, 13]), require some sequence of positive pooled results to correctly identify Donald as infected. Consider the pooling scheme of [13]: If the first pool yields a positive result, it is split in two. Then the splitting is repeated until resulting poolss are negative or individuals are tested separately. With an initial pool size of 32, Donald will necessarily have to test positive in pools of size 32, 16, 8, 4 and 2, as well as in a single test, for the scheme to correctly identify him as infected. Compare this to the Dorfman scheme that requires a positive test in a pool of size N = 8, and an additional single positive test to identify Donald as infected. The pooling scheme of [13] will necessarily yield more false-nagetives than Dorfman pooling — there are additional places for it to fail.
As mentioned in [1], introducing a positive dependence within a pool decreases the false-positive rate. In the extreme case, consider a fully connected pool, where one infection implies the entire pool is infected. In this case, a calculation analogous to the one conducted above recovers the initial false-negative rate Pfn. Interestingly, pooling was also noted to have increased through-put when infection probabilities are dependent between the pooled individuals [1], providing another advantage to sampling dependent individuals in pooling schemes.
To conclude, pooling is an important technique which can facilitate testing throughput in a cost-effective manner. Nevertheless, a substantial increase in pooling schemes’ false-negative rates can be expected. Such an increase in pooling schemes’ false-negative rates has crucial implications for controlling the spread of COVID-19.
Data Availability
No data was used in the manuscript.