Statistical Assessment of Biomarker Replicability using MAJAR Method

MAJAR workflow

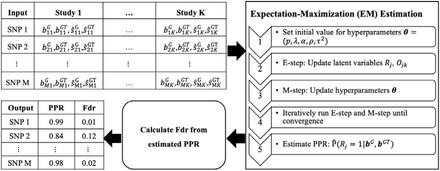
MAJAR is a statistical method proposed for jointly testing prognostic and predictive effects and assessing the replicability of identified biomarkers without using an independent cohort in the framework of meta-analysis. It can be used for analysis of general biomarkers such as clinical biomarkers, oncology biomarkers, genomics biomarkers, and other biomarkers. In this paper, we introduce MAJAR under the setting of analyzing genetic biomarkers in the context of PGx GWAS. The whole workflow of the proposed MAJAR method is summarized in Figure 1. The inputs of MAJAR are summary statistics of M SNPs from K studies. We denote the genotype (G) and genotype-by-treatment interaction (GT) effect size estimates as b_jk,G and b_jk,GT and the standard errors as s_jk,G and s_jk,GT for SNP j in study k (k=1, 2, …, K; j=1, 2, …, M). MAJAR takes the input summary statistics from K studies and uses an EM algorithm to estimate hyperparameters formulated in a two-dimensional hierarchical mixture model and calculates PPR for each SNP. For inference of replicable SNPs, MAJAR further converts the PPRs into Bayesian False discovery rate (Fdr) values using a joint local false discovery rate (Jlfdr) method previously proposed [20] to control the global Fdr under a specific threshold.

• Download figure
• Open in new tab

Figure 1. Overview of MAJAR method.

Left top table: the summary statistics data from K studies including the genotype (G) and genotype-by-treatment (GT) effect size estimates and, and the standard errors as and for SNP j in study k (k = 1, 2, …, K; j = 1, 2, …, M). This summary statistics data is served as the input of the EM algorithm. Right panel: the EM algorithm procedure to estimate the parameters and posterior probability of replicability (PPR) for each SNP. Left bottom box: after the PPRs are estimated, the Fdr can be further calculated using the Jlfdr method. Left bottom table: the MAJAR algorithm outputs both the PPR and Fdr for each SNP.

Two-dimensional hierarchical mixture model

MAJAR is a two-dimensional hierarchical mixture model extended from MAMBA [12] by considering biomarkers’ prognostic (G) and predictive (GT) effects simultaneously. In the hierarchical mixture model, there are two sets of latent variables R_j and O_jk, where R_j is the indicator that SNP j has a real non-zero effect and O_jk is the indicator that a non-replicable zero effect SNP j is a spuriously associated outlier in study k. There are two assumptions for latent variables. 1) We assume replicable non-zero effect SNP j has the latent association status R_j in terms of the joint effect of G and GT effects, where R_j follows a Bernoulli distribution with the proportion of replicable non-zero effect SNPs being p. 2) We assume non-replicable zero effect SNP j in study k has the latent outlier status O_jk, where O_jk follows a Bernoulli distribution with the proportion of outlier zero-effect SNPs being λ. Given R_j and O_jk, we assume that G and GT effect size estimates follow a mixture of bivariate normal distribution. When SNP j has a replicable non-zero effect, the mean of the bivariate normal distribution is 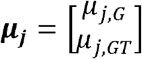. When SNP j is a non-replicable variant, the mean of the bivariate normal distribution is 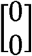. For spurious associations from non-replicable zero-effect variants, we further use an inflation factor α to characterize the extent of inflation in the observed effect sizes. To capture the correlation between G and GT, we assume the prior distribution of true effect sizes μ_j follows a bivariate normal distribution, e.g., MVN(0, Ω), where 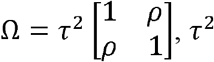is the variance of true effect sizes of G and GT, and ρ is the correlation between true effect sizes of G and GT.

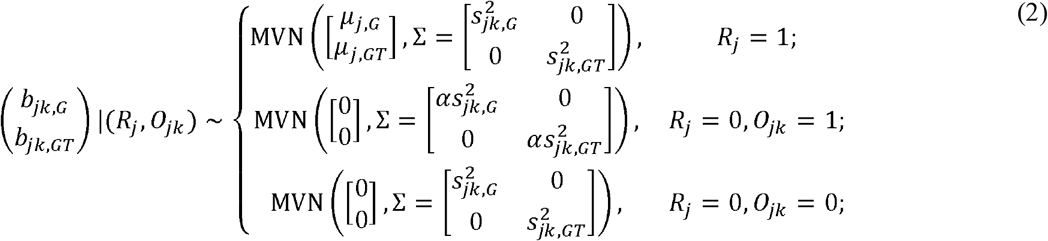
Together, we can summarize our MAJAR two-dimensional hierarchical mixture model as: where α is an inflation factor that captures the extent of inflation in the observed effect sizes for outlier summary statistics and we denote the hyperparameters of MAJAR as θ = (p, λ, α, τ², ρ).

Estimation - EM algorithm

We develop an EM algorithm for hyperparameter estimation that is computationally efficient when handling variants on a genome-wide scale. To estimate the parameters, the EM algorithm runs Expectation (E-step) and Maximization (M-step) iteratively until convergence. At round t, it updates the latent variables 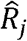and 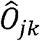by their posterior probabilities given the parameter estimates at iteration t − 1, which is shown in equations 4 and 5. 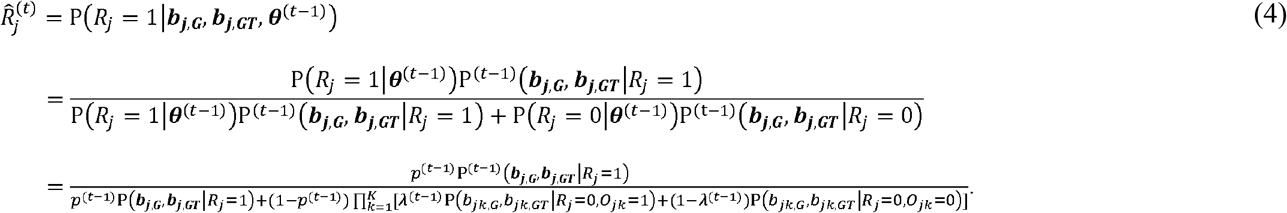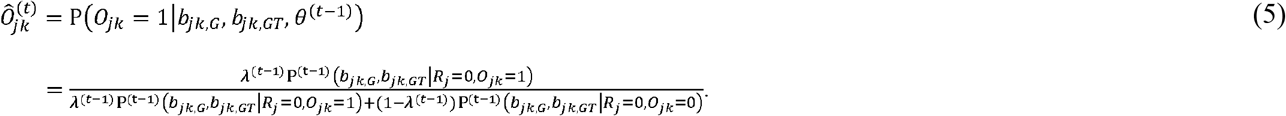In the M-step, the hyperprior parameters θ are updated by maximizing the expected log-likelihood calculated from the E-step. For p, λ and α, there are explicit solutions, which are: As there is no explicit solution for (τ², ρ), we utilize the unconstrained quasi-Newton method optimizer nlminb() [21] implemented in R [22] to optimize the two parameters by maximizing the terms related to them in the expected complete data log-likelihood (ll) (equation 9). More details of the derivations are described in the Supplementary Methods Section 1 (Optimizing (τ², ρ) parameters). 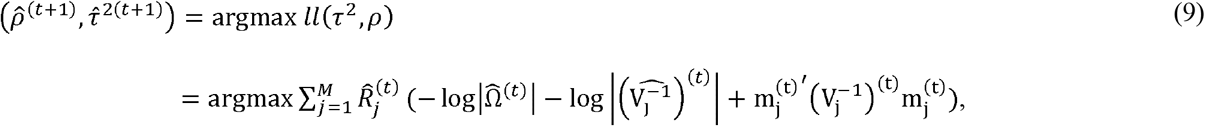where 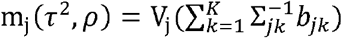and .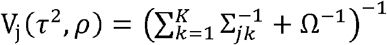

After the EM algorithm converges and the hyperparameters are estimated, the PPRs of the tested SNPs can be estimated directly from the output of E-step as

Inference - Jlfdr approach

Jlfdr is defined as the posterior probability of a null hypothesis given the observed summary statistics. Here, the summary statistics are and 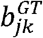in the MAJAR model. 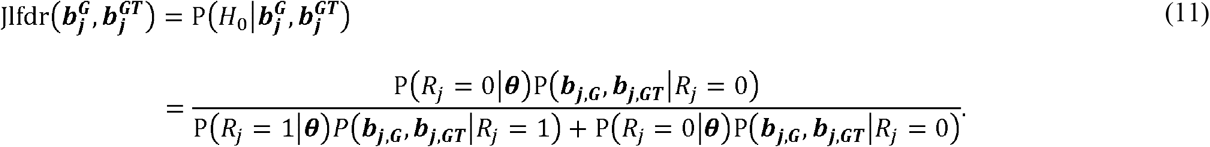Jiang and Yu [20] have shown the relationship between Jlfdr and Fdr is 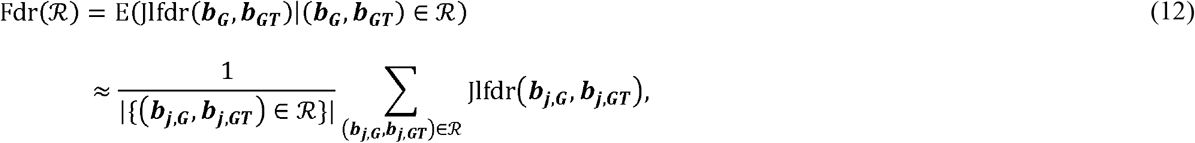where the rejection region ℛ is the set of two-dimensional vectors b_j,G, b _j,GT) that the null hypothesis can be rejected based on specific rejection criteria. Based on the derivation in the original method [20], the most powerful rejection region for a given Fdr level q is {Jlfdr (b_j,G, b _j,GT ≤ t (q)}, where t (q) is a threshold that can be determined by Fdr(ℛ^a) = q. The threshold of t(q) can be determined by first sorting the Jlfdr values of all tested SNPs in ascending order with the a-th Jlfdr value as Jlfdr^a, and then approximating the Fdr of the region as Denote c=max{a| Fdr(ℛ^a) ≤ q)}, then the Jlfdr threshold t(q) is Jldfr^c. The decision rule is to reject all SNPs with Jlfdr .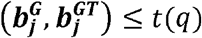

Fast Implementation of the MAJAR Algorithm

Motivated by MAMBA [12], we have implemented MAJAR with three strategies to increase its computational efficiency: 1) using the mcapply() function in the R parallel package for multi-core computation to update O_jk by running M SNPs in parallel; 2) implementation of E-step functions using C++ through the R Rcpp package [23,24] and M-step optimization function (equation 9) with the R TMB package [24]; and 3) unbounding the parameter space of (τ², ρ) when maximizing the expected log-likelihood. Specifically for 2) the MakeADFun function in the package can calculate first and second order derivatives of the likelihood function written in C++ and the function and its derivative can be called from R. For 3), we map ρ to arctanh (ρ) to unbound the parameter space from (−1, 1) to (−Inf, Inf), and map τ² to log τ² to unbound the parameter space from (0, Inf) to (−Inf, Inf). We conducted a benchmark analysis to compare the computation time of our method with and without implementing these strategies. The fast implementation of our software can be accessed from our GitHub webpage https://github.com/JustinaXie/MAJAR.

Simulation studies

We conducted extensive simulation studies to benchmark the performance of MAJAR with other commonly used meta-analysis and replicability analysis methods including meta-analysis fixed effect model (FE), meta-analysis random effect model (RE), and MAMBA. We first checked whether MAJAR can estimate the parameters accurately under the ground truth model and then compared the power performance of MAJAR with MAMBA, FE, and RE under the data generation process of MAJAR, FE and RE’s ground truth models, respectively. Given FE, RE, and MAMBA can only perform marginal analysis instead of conditional or joint effect analysis, we inferred replicable SNPs by testing only the marginal G effect for these three methods. We also verified whether MAJAR simplifies into MAMBA when only the G effect exists.

We randomly simulated 5,000 SNPs in total and varied the number of studies K in the meta-analysis from 2, 5, to 10. We used standard errors estimated from the GWAS summary statistics of our real (IMPROVE-IT) PGx data. The proportion of replicable non-zero effect SNPs p was set to 0.05, 0.1 or 0.2. According to the relationship between the variance of SNPs (τ²) and the heritability 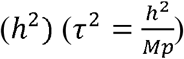[25], we varied τ² by setting h² from 0.1, 0.3 to 0.5.

Under the data generation process of the MAJAR ground truth model, we set the proportion of non-replicable zero-effect SNPs λ to 0.1 and varied the inflation factor α from 1, 2, 5, to 15. We also tested the robustness of MAJAR under different correlation settings of G and GT by varying the correlation parameter p from -0.75, -0.25, 0, 0.25, to 0.75. The simulation procedure under MAJAR’s ground truth model includes three steps. In the first step, we simulated the latent variables R_j ∼ Bernoulli (p) and O_jk ∼ Bernoulli (λ). In the second step, we simulated the true effect sizes 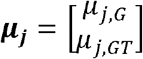with a spike-and-slab prior. That is, when R_j = 0, μ_j = 0; and when R_j = 1, In the third step, we simulated the effect size estimates 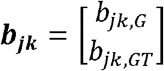from the mixture bivariate normal distribution according to equation 2. Simulation details under the FE and RE data generation process are introduced in Supplementary Methods Section 2-3. Robustness analysis was also conducted under an extended model of MAJAR in which the variance τ² of G and GT are not the same (i.e., ).

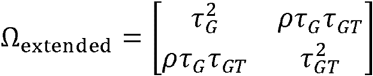We replicated the simulation 100 times under each setting. The false discovery proportion (FDP) was defined as the proportion of false rejections and the expected value of FDP given the number of rejections is larger than 0. We set the Fdr threshold as 0.05 for discovery of replicable SNPs. Computation time was benchmarked using 2.4 GHz Intel Core i5 with 4 parallel cores for all methods compared.

Application to IMPROVE-IT PGx GWAS data

We applied MAJAR to jointly testing the prognostic and predictive effects on the low-density lipoprotein cholesterol (LDL-C) log-fold change at 1 month in a PGx GWAS summary statistics data. This data was from the IMPROVE-IT (IMProved Reduction of Outcomes: Vytroin Efficacy International Trial, clinical trial registry number: NCT00202878) study. IMPROVE-IT is a multi-center, double-blind, phase 3b randomized trial to establish the efficacy and safety of Vytorin (ezetimibe□+□simvastatin tablet) versus simvastatin monotherapy in high-risk subjects [16]. A detailed introduction of the study population, genotyping, genotype quality control (QC), and imputation for the GWAS analyses were described in previous studies [17,18]. After variant-level QC and imputation, there were 9,407,967 variants and 6,502 subjects available for analysis. After filtering out subjects who had a cardiovascular event prior to our analysis time point (month 1) to avoid interference unrelated to treatment on LDL-C, a total of 5,661 unrelated European subjects were included in the final analysis. Similar to the simulations, we also applied MAMBA to testing the prognostic (G) effect and predictive (GT) effect separately in the analysis of the IMPROVE-IT PGx GWAS summary statistics data.

Due to the lack of PGx GWAS data from multiple studies with the same endpoint, we proposed an alternative strategy to analyze the IMPROVE-IT data by randomly splitting the whole cohort into five folds. We conducted GWAS on each fold and used the summary statistics from each fold, only keeping variants with MAF > 0.01 as input for MAJAR. To boost the computational speed, we adopted a similar strategy as MAMBA [12] to clump variants with suggestive evidence from a reference method, prune variants with relatively low evidence, and then combine variants together in the two sets. Cauchy combination test (CCT) [26] was used to get combined p -values, which were further used as a reference for clumping and pruning in PLINK 1.90. For clumping, we used parameters “–clump-p1 1e-4 –clump-kb 1000 –clump-r2 0.1”. For pruning, we used 1000 genome European samples [27] as a reference panel with parameters “–indep-pairwise 1000 kb 1 0.1” and matched the pruned sets with the IMPROVE-IT variants. To ensure the combined sets of variants are not within the same linkage equilibrium (LD) block, we removed all pruned variants in 1M bp within clumped variants. Then, we ran MAJAR, MAMBA, FE, and RE on the variants left for each chromosome to allow different parameters estimated for each chromosome. In practice, we set the inflation factor α ≥1 for both MAJAR and MAMBA and set the initial hyperparameter values of MAMBA (p, λ, α τ²) the same as those of MAJAR to make a fair comparison. We followed the same penalty strategy from previous studies [20,28]. We also conducted the interaction test of the GT effect with MAMBA by using b_jk and s_jk,GT as input without conditioning on the G effect. We further pooled PPRs from all chromosomes, converted them to Fdr values, and compared the results with CCT p-values and the pooled GWAS 2df p-values [17]. In addition, to examine the robustness of the results, we also conducted a sensitivity analysis using a five-fold cross-validation procedure, for example, by leaving one fold out from the five folds and repeating the same analytical procedures on the remaining four folds.

Simulation results: Fdr and power under ground truth model

Before evaluating the Fdr and power under the ground truth model (i.e., data generation process or DGP = MAJAR), we first checked whether MAJAR can accurately estimate the true effect sizes (μ_G, μ_GT) and hyperparameters (p, λ, α, ρ, τ²). The simulation results are summarized in Figure S1, which shows that MAJAR has generally unbiased estimates under different combinations of the number of studies and the heritability. It is worth noting that the mean square error (MSE) of μ_G and μ_GT slightly increased when the heritability increased. This is as expected since the magnitude of genetic effect sizes was larger when the genotype explained more variances in the phenotype. Overall, the MSEs were very small (i.e., close to 0 at 10⁻³ level), indicating that MAJAR can accurately estimate the true effect sizes and hyperparameters.

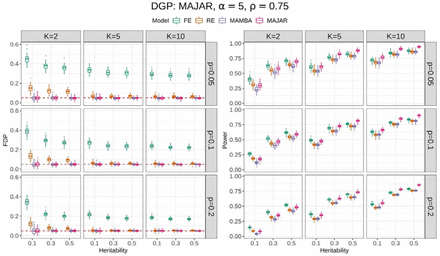
Given the unbiased estimation, we further visualized the Fdr and power results for comparing FE, RE, MAMBA, and MAJAR under different combinations of the number of studies K, the proportion of replicable non-zero effect SNPs p, and the heritability h² by fixing inflation factor α at 5 and ρ at 0.75 (Figure 2). The simulation results in Figure 2 showed that FE was not able to control Fdr at the desired threshold of 0.05 under all settings, and RE also had slight inflation when both the study number K and the heritability h² were small. In contrast, both MAMBA and MAJAR controlled Fdr well.

• Download figure
• Open in new tab

Figure 2. Simulation results of FDP and power while comparing FE, RE, MAMBA, and MAJAR under MAJAR’s ground truth model.

The left panel is for the FDP (false discovery proportion) performance, and the right panel is for the power performance. For each panel, the columns represent the number of studies K, and the rows represent the proportion of replicable non-zero effect SNPs p. Each panel shows the FDP and power (y-axis) with increasing heritability h² (x-axis) under different settings of K and p. The performance of each method in 100 replications under each simulation setting is visualized by the colored boxplots. The red dashed line in the FDP panel indicates the target Fdr threshold of 0.05.

For power comparisons, FE was not considered for the method comparison given its severe Fdr inflation (Figure 2, left panel). Overall, RE had comparable power to MAMBA, while MAJAR consistently had the best power among all circumstances (Figure 2, right panel). The power increased for all models as the study number K increased. However, the power improvement of MAJAR over other methods was even greater. For example, when K = 2, the power increase from RE to MAJAR was between 2.6% and 10.0%; when K = 10, such power increase was between 9.8% and 16.2% in terms of the median values under different combinations of p and h². This indicated that MAJAR was more effective in leveraging information across multiple studies than other methods by modeling both prognostic and predictive effects. With the increase of the proportion of replicable non-zero effect SNPs p, the power decreased for all models. This is because the signal of non-zero effect SNPs became weaker given the relationship between the variance of true effect sizes 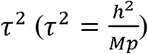. In that condition, we observed that the power of MAJAR decreased much slower than RE and MAMBA (e.g., MAJAR outperformed RE by increasing the power between 2.6% and 11.7% when p = 0.05 and between 8.5% and 16.2% when p = 0.2 in terms of the median values under different combinations of K and h²), suggesting that MAJAR is more robust to highly polygenic genetic architectures with small signal-to-noise ratio. Lastly, when the heritability increased, MAJAR was also superior to other methods (e.g., MAJAR outperformed RE by increasing the power between 2.6% and 13.1% when h² = 0.1 and between 6.1% and 16.2% when h² = 0.5 in terms of the median values under different combinations of K and p).

Simulation results: Fdr and power under other DGPs

In the previous section, we showed that MAJAR had its advantages over other methods under the ground truth model (i.e., when DGP = MAJAR). In this section, we explore whether MAJAR still outperforms the existing methods under other DGPs. Under the data generation processes of FE and RE, we visualized the simulation comparison results of Fdr and power under different settings K, p and h² and fixed ρ at 0.75 (Figure S2-S3). For data generated under FE, all methods controlled Fdr well except that the RE method tended to be a little conservative. The power performance of MAMBA was comparable to the FE method and MAJAR performed the best. For data generated under RE, the FE method had severe Fdr inflation, while other methods generally controlled Fdr well. MAMBA yielded better or comparable performance to RE, while MAJAR provided better performance than MAMBA. In a nutshell, MAMBA and MAJAR were more robust than FE and RE in terms of Fdr control under different DGPs, with MAJAR having superior power across different scenarios. Under the data generation process of MAMBA with prognostic effect only, we observed that MAJAR had a very similar false discovery proportion (FDP) and power performance as MAMBA (Figure S4). Overall, the power of MAJAR was slightly smaller than MAMBA when the number of studies was small. This is as expected since MAJAR, using a two-dimensional hierarchical mixture model to estimate prognostic and predictive effects simultaneously, would inevitably include noises when the predictive effect didn’t exist. When there were only G effects (i.e., without any GT interaction effects) and the number of studies was large, MAJAR had very similar power as MAMBA.

Simulation results: sensitivity analyses

To test the robustness of MAJAR with regards to different correlations between G and GT effects ρ, we ran the simulations by following the MAJAR data generation process and fixing α at 5 and h² at 0.3 and compared the power performance with increasing values of ρ (Figure S5). The results showed that the power of MAJAR first increased and then decreased with the increase of ρ and MAJAR had slightly better power performance when the correlation was weak regardless of the correlation directions (i.e., with a small absolute correlation). Overall, MAJAR was robust to the varied correlations between G and GT effect sizes.

To test the robustness of MAJAR with regards to different outlier inflation factor α, we fixed ρ at 0.75 and compared the power performance under different α (Figure S6). MAJAR controlled Fdr well under all settings. The power of MAJAR decreased with increasing α when the number of studies was small. This indicated that it was hard for MAJAR to differentiate the outliers among studies when there were only a small number of studies. When the number of studies was larger, MAJAR’s power under different α became comparable.

Under the MAJAR ground truth model, we assumed the prognostic (G) and predictive (GT) effect sizes were on the same scale by setting the variances of the two effects to the same τ² value as in our previous simulation analyses. We also tested the robustness of our method under an extended model of MAJAR where variances of G and GT were different. In this simulation, we fixed the value of the heritability of 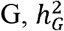, so the increase in the ratio 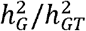means a decrease in the heritability of 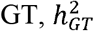. The simulation results are summarized in Figure S7. In summary, the simulation results showed that MAJAR had slight Fdr inflation and slightly decreased power when K = 2 and 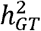was much smaller than 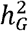(i.e., the assumption was violated). With the increase of K, MAJAR had improved power with well-controlled Fdr, regardless of whether the assumption was violated or not.

Application to IMPROVE-IT PGx GWAS data

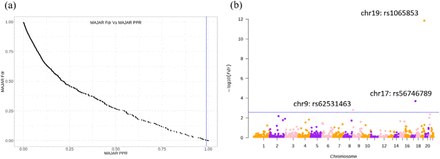
After applying MAJAR to IMPROVE-IT PGx GWAS summary statistics data using our proposed five-fold strategy, we summarized the whole genome SNPs’ PPR and their corresponding Fdr in a scatter plot (Figure 3a) and further visualized the Fdr results in a Manhattan plot (Figure 3b). We determined the Fdr cutoff that corresponded to PPR > 0.99 (Figure 3a) and drew the corresponding blue line (Fdr < 0.003) on the Manhattan plot. In total, we observed 3 variants (rs1065853, rs56746789, rs62531463) under a stringent threshold of PPR > 0.99 (i.e., Fdr < 0.003) (Table 1). The most significantly associated variant (rs1065853) was located in APOE/APOC1, which is a well-known locus that is associated with response to statins and involved in lipid metabolism and drug transport [29,30]. This variant had very high MAMBA-G (MAMBA using summary statistics of G effect only as input) PPR (PPR=1) and was also a strong signal in the pooled GWAS 2df test (p = 1.09 × 10⁻⁵¹). The other two variants with PPR > 0.99 had relatively high PPRs for both MAMBA-G effects (rs56746789 PPR = 0.832; rs62531463 PPR = 0.638) and MAMBA-GT effect (rs56746789 PPR = 0.510; rs62531463 PPR = 0.439), indicating the boosted power of replicability from the GT effect added. The two variants are located in locus LINC01482 and gene KANK1, respectively. By searching the LINC01482 locus in the GWAS catalog (https://www.ebi.ac.uk/gwas/), we found there were in total 53 studies related to this locus and 33 associations between SNPs within this locus and LDL, HDL, and other lipid-related traits. By searching the KANK1 locus on the GWAS catalog, we found there were in total 33 studies related to this locus and 2 associations related to lipid measurement. Previous studies have also reported the loci in KANK2, KANK1’s close paralog, are associated with LDL-C [31,32].

• Download figure
• Open in new tab

Figure 3. MAJAR whole genome meta-analysis results from the analysis of IMPROVE-IT GWAS summary statistics data.

(a) Relationship between MAJAR Fdr and MAJAR PPR. The x-axis represents MAJAR PPR, and the y-axis represents MAJAR Fdr. The vertical blue line represents MAJAR PPR=0.99. (b) Manhattan plot for all tested variants. The y-axis represents the values, and the x-axis shows the genome position of all variants. The blue horizontal line represents the PPR threshold of 0.99 (Fdr = 0.003) determined from the relationship between Fdr and PPR shown in the left figure.

We further tested the robustness of the results in the framework of five-fold cross-validation after leaving one fold out from the five folds each time. We visualized the robustness analysis results based on the 5-fold cross-validation procedure in an upset plot (Figure S8). From the bottom right part of the upset plot, all three identified variants were consistently selected in at least 4 out of the 5 iterations. This demonstrated the robustness of the top 3 variants identified by MAJAR in the IMPROVE-IT data analysis. We identified 10 additional variants under the threshold of Fdr < 0.05 (Table S1) including two variants on chromosome 21 (rs76451912, rs282368), three variants on chromosome 2 (rs4954144, 235349598-C-T, rs35421171), two variants on chromosome 15 (rs28510330, rs201822759), and one each on chromosome 4 (rs1351220), chromosome 8 (rs35903937), and chromosome 9 (rs61381472). rs76451912 is located in the noncoding region. The nearest coding gene is ADAMTS5, which has been reported to have multiple associated SNPs with blood protein measurement in two studies [33,34] and a disintegrin and metalloproteinase with thrombospondin motifs 5 measurement, the proteolytic activity of which has been shown to reduce the LDL binding ability of biglycan and releases LDLs from human aortic lesions [35], in three studies [36–38]. rs4954144 is an intron variant in MGAT5, which has been reported to have multiple associated SNPs with multiple cholesterol related measurements [39]. The remaining top hits identified may represent novel genetic associations, which need further interpretation and exploration. The evidence of mapped genes of top variants downloaded from the GWAS catalog is shown in Table S2.

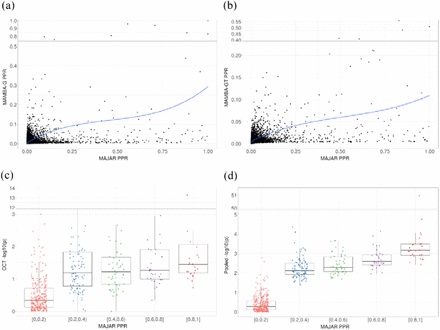
We also compared the PPR distributions among MAJAR, MAMBA-G, and MAMBA using summary statistics of GT effect only as input (MAMBA-GT). All three PPRs showed right-skewed distributions with long right tails, indicating that most SNPs were not replicable (non-zero effect) signals. The corresponding frequency dropped more smoothly when PPR increased for MAJAR method, compared to MAMBA-G and MAMBA-GT (Figure S9). We visualized the overlapping results among MAJAR, MAMBA-G, MAMBA-GT, and the 2df test from the pooled GWAS in terms of signal detection using Venn diagrams (Figure S10). Under the condition that the pooled GWAS 2df test p-values < 1 × 10³, MAJAR identified three overlapping variants (PPR > 0.99) with the pooled GWAS results, out of which one signal is also significant in the MAMBA-G analysis (i.e., PPR > 0.99). MAMBA-GT did not identify any variants with PPR > 0.99. After we used a more stringent threshold of the 2df test p-value < 1 × 10⁻⁴ for the pooled GWAS analysis, MAJAR identified two out of three previously identified overlapping variants with the pooled GWAS. Moreover, we checked the pair-wise consistencies between MAJAR PPRs and MAMBA-G PPRs, MAMBA-GT PPRs, − log_l0 p-values from the pooled GWAS and − log_l0 p -values from the CCT test, respectively. From the scatter plots, we observed clearly positive correlations between the PPR results from MAJAR and the results from existing methods (Figure 4). This also indicates the consistency trend of the signals discovered by different methods.

• Download figure
• Open in new tab

Figure 4. Comparison of MAMBA-G PPR, MAMBA-GT PPR, CCT p-values, pooled GWAS 2df test p-values versus MAJAR PPR.

(a) Scatter plot of MAMBA-G PPRs versus MAJAR PPRs. The blue curve is fitted by the LOWESS smoother. (b) Scatter plot of MAMBA-GT PPRs versus MAJAR PPRs. The blue curve is fitted by the LOWESS smoother. (c) Scatter plot of CCT p-values and MAJAR PPRs. Variants are categorized and colored by five different bins of MAJAR PPRs. The boxplots demonstrate the distribution of CCT p-values under five different bins of MAJAR PPRs. (d) Scatter plot of pooled GWAS 2df p-values and MAJAR PPRs. Variants are categorized and colored by five different bins of MAJAR PPRs. The boxplots demonstrate the distribution of pooled GWAS 2df p-values under five different bins of MAJAR PPRs.

Computation time

We compared the computation time of MAJAR with FE, RE, and MAMBA under the MAJAR data generation process (Materials and Methods). Empirically, we observed the computational bottleneck of MAJAR’s algorithm is the estimation of (τ², ρ) in the M-step. When only R code is used to implement the algorithm, the computation time is much slower than the efficient implementation with parallel computing and C++. The computation time comparison results were summarized in Figure S11. From this figure, we observed that the FE model was the fastest under all simulation settings followed by RE, which is due to its model simplicity. MAMBA was slower than FE and RE. This might be due to the relatively more stringent convergence criteria of the algorithm. The fast version of MAJAR (partly written in C++ and implemented with 4 cores in parallel) was comparable to RE with the increase of K. Theoretically speaking, the proposed MAJAR model (i.e., two-dimensional hierarchical mixture model) was more complicated than MAMBA since it has more hyperparameters to be estimated in the EM algorithm. Figure S11 shows that MAJAR runs much faster than MAMBA, which indicates that our fast implementation strategies can indeed improve the computational efficiency. In fact, MAJAR without fast implementation (written in R and implemented with only one core) was much slower than the other methods: MAJAR without fast implementation was around seven times slower than MAMBA and 20 times slower than MAJAR with fast implementation. Under most simulation settings, the fast version of MAJAR could perform the test for 5,000 SNPs within a minute.

For the IMPROVE-IT real data application, we conducted the analysis by parallelizing the 22 chromosomes, so that the time cost is the computation time of the largest chromosome. In our data, the chromosome that required the longest time was chromosome 2 with 11,213 SNPs after pruning and clumping. The running time of MAJAR was 9.3 minutes, MAMBA-G 34.7 minutes, and MAMBA-GT 35.4 minutes. These results demonstrate that MAJAR can efficiently conduct the assessment of biomarker replicability in studies with a large number of biomarkers such as in PGx GWAS.