Abstract
Drug resistance is a problem in many pathogens, including viruses, bacteria, fungi and parasites [1]. While overall, levels of resistance have risen in recent decades, there are many examples where after an initial rise, levels of resistance have stabilized [2–6]. The stable coexistence of resistance and susceptibility has proven hard to explain – in most evolutionary models, either resistance or susceptibility ultimately “wins” and takes over the population [2,3,7–9]. Here, we show that a simple stochastic model, mathematically akin to mutation-selection balance theory, can explain several key observations about drug resistance: (1) the stable coexistence of resistant and susceptible strains (2) at levels that depend on population-level drug usage and (3) with resistance often due to many different strains (resistance is present on many different genetic backgrounds). The model works for resistance due to both mutations or horizontal gene transfer (HGT). It predicts that new resistant strains should continuously appear (through mutation or HGT and positive selection within treated hosts) and disappear (due to the cost of resistance). The result is that while resistance is stable, which strains carry resistance is constantly changing. We used data on 37,000 E. coli isolates to test this prediction for a known resistance mutation and a resistance gene in the UK and found that the data are consistent with the prediction. Having a model that explains the dynamics of drug resistance will allow us to plan science-backed interventions to reduce the burden of drug resistance. Next, it will be of interest to test our model on data from different drug-pathogen combinations and to estimate model parameters for these drug–pathogen combinations in different geographic regions with varying levels of drug use. It will then be possible to predict the results of interventions, especially drug restriction policies and increase our understanding of whether and how fast such restrictions should result in reduced resistance [10,11].
Introduction
Drug resistance is common in viruses (HIV), bacteria (S. aureus, E. coli, M. tuberculosis), parasites (P. falciparum) and fungi (Candida species), making it a major public health threat [1]. What can we do to prevent the rise of drug-resistant strains? Or to revert the trend if the level of resistance is already high? To plan successful science-backed interventions, we must understand what determines the level of drug resistance in a given pathogen. Therefore, a need exists for better models to explain current resistance levels, predict how resistance rates will change over time and identify which interventions would most reduce the burden of resistance. Here, we present a simple model that does all of these things.
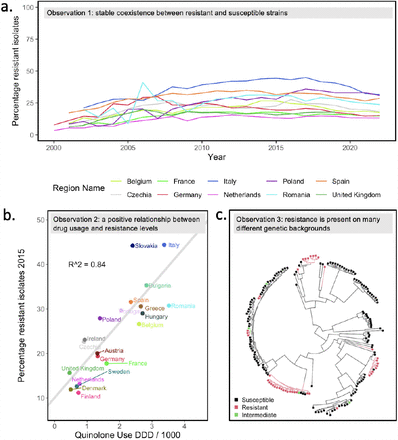
Any model that might be used to predict drug resistance levels for different pathogens must be able to explain several observations that are currently not well explained [2,3,12]. First, while overall drug resistance has increased over the years, in many cases, an initial increase in resistance is followed by stable coexistence between drug-resistant and drug-sensitive strains. For an example, see Figure 1A on fluoroquinolone resistance in E. coli in Europe. Other examples of stable coexistence of resistant and susceptible strains can be found in S. pneumoniae [2,3], S. aureus [4] and HIV [5,6]). Second, a positive linear relationship has been observed between treatment intensity at the population level and drug resistance levels [13](Figure 1B). And third, many different resistant strains (i.e., resistance on different genetic backgrounds) often segregate at the same time in a pathogen population [5,14] (see Figure 1C for an example of resistance to the fluoroquinolone drug ciprofloxacin in E. coli in the UK; resistance appears repeatedly on the phylogenetic tree).
a. Observation 1. Typically, an initial increase in resistance is followed by stable coexistence between drug-resistant and drug-sensitive strains. Each line depicts a quinolone resistant E. coli strain over two decades in the 10 most populous countries (formerly) in the European Union (EU). b. Observation 2. Treatment intensity at the population level is correlated with drug resistance levels. A strong positive correlation exists between quinolone usage and quinolone resistance levels in 17 countries in the EU. Publicly available data from the Surveillance Atlas of Infectious Diseases were used to create Figures 1a and 1b. c. Observation 3. Many different resistant strains often segregate at the same time. Quinolone (specifically ciprofloxacine) resistance in bacteremia patients in the UK is due to many different origins of resistance (here phylogroup D and F are shown). Data from [13], figure reproduced from [14].
The second observation feels intuitive to most of us: If we use more drugs, we get more drug resistance. But the first observation, of stable coexistence, is puzzling: if there is selection for drug resistance, why doesn’t the level of resistance keep increasing until it reaches 100%? The third observation, of resistance in many strains or genetic backgrounds, can be seen in many phylogenetic trees in articles about drug resistance, but usually does not receive a lot of attention. For example, in a large study of HIV isolates in Northern California, Rhee and colleagues found 82 phylogenetic clusters with one or more drug-resistance mutations [5]. In an E. coli dataset from the UK, 31 independent phylogenetic clusters with ciprofloxacin-resistant strains were found [15], and Casali and colleagues found 106 independent phylogenetic clusters with pyrazinamide resistance in M. tuberculosis [16]. These results show that resistance has evolved de novo or been acquired through horizontal gene transfer (HGT) many times [17,18].
Several different explanations have been put forward to explain the coexistence of resistance and susceptibility and the positive relationship between treatment and resistance levels [2,3]. These explanations have usually focused on mechanisms that require population structure or coinfection to create stabilizing selection [2,3,7–9]. We propose a simpler model akin to mutation-selection balance. Our model requires few assumptions, which means it can be applicable to a large variety of pathogens, and few parameters, which makes it easy to use.
We call the model “resistance acquisition and negative selection balance,” and will show that it can explain all three key observations about drug resistance listed previously. Note that when resistance is due to HGT, we don’t aim to explain why genetic elements that confer drug resistance exist or how they evolved, but rather why they are carried by a stable frequency of strains in pathogen populations.
The resistance acquisition – negative selection balance model
Our main goal is to determine whether a model based on the classic mutation-selection balance theory can explain three striking observations of drug resistance at the population level: (1) a stable coexistence of resistance and susceptibility, (2) a positive relationship between drug usage and resistance levels, and (3) the simultaneous existence of many drug-resistant strains. Here, we develop a mathematical model that can explain the first two explanations for resistance due to de novo mutation or HGT, and then we run individual-based simulations that keep track of different resistant strains and explain the third observation. Finally, we analyze a large number of E. coli genomes over 15 years to visually compare predicted and observed patterns of resistance.
We base our model on classic mutation-selection balance theory because this model has already been used to explain a stable level of deleterious mutations and the existence of multiple alleles that carry a deleterious mutation [19,20]. Mutation-selection balance is a well-understood dynamic equilibrium, and we can borrow mathematical results from that theory directly here [21,22]. Mutation-selection balance has not received much attention as a potential explanation for drug resistance patterns because it is often believed to lead to resistance frequencies close to 0% (which is not usually observed in real life), and in the basic form, the model only considers negative selection (against resistance) and not positive selection (for resistance). Because it is clear that positive selection for drug resistance plays a role in the frequency of resistant strains (as evidenced by the second observation: more drugs lead to more resistance), we propose a version of mutation-selection balance that includes positive selection within treated hosts. It can explain stable resistant levels at any frequency.
In the basic mutation-selection balance model, mutation creates deleterious alleles at probability μ per individual per generation and these alleles reduce the fitness of the individual carrying them by selection coefficient s, see Table 1. Standard population genetic theory predicts that the deleterious allele frequency is μ/s [21]. Population genetic theory can also be used to predict the number of different mutations that segregate at any one time [19,20,23] and the time it takes for this equilibrium to be reached after the system is perturbed [24].
To apply mutation-selection equilibrium theory to the problem of drug resistance, we have to make several adjustments and assumptions, but it is actually simple to recover the main mathematical result of the equilibrium level of resistance. First, we treat the population of the pathogen in an infected host as one pathogen individual. This assumption is valid if a strong transmission bottleneck occurs for each infection. Next, we assume that such “pathogen individuals” have a probability, t·e, per time step, to be treated (t) and evolve to become resistant (e). The treatment parameter t is the probability that the host is treated and the evolution parameter e is the probability that the within-host pathogen population evolves to become resistant through mutation or the acquisition of a genetic element, given that the host is treated. Mathematically, t·e plays the role of the mutation parameter μ in the standard model. Next, we assume that resistance comes with a mild cost, c, which can be understood as a reduction in R0 compared to the R0 of the susceptible pathogen strain. The cost parameter, c, determines how likely the resistant strain is to be transmitted to other hosts [25]. Mathematically, c plays the role of s in the standard model. We call the fraction of pathogen “individuals” that is resistant (equivalent to the fraction of resistant infections out of all infections): f. Only susceptible pathogen individuals (1-f of the population) can evolve to become resistant. Under this model, the frequency of resistant strains, f, will increase at rate t·e*(1-f) through positive selection within hosts and be reduced by negative selection at rate -c*f (1-f). Thus the change in frequency can be written as:
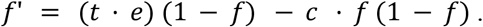
An equilibrium will be reached when
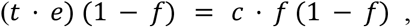which means that the predicted frequency of resistance at the host population level will be:
f = (t · e)/(c), see Figure 2. This result explains both the stability of the level of resistance and the linear relationship between treatment levels (through t) and the level of resistance.
Higher levels of treatment lead to higher values of t*e, consistent with Key Observation 2 about drug resistance. Strains acquire resistance by mutation or through horizontal gene transfer. Resistant strains can be transmitted to other hosts, with an R0 that is reduced by (1-c) compared to the R0 of susceptible strains.
Simulations in a SIRS model
To gain a better understanding of the resistance acquisition – negative selection balance model and to determine whether the results satisfied key observation #3, we ran individual-based simulations using a Susceptible, Infected, Recovered and Susceptible hosts (SIRS) model. A SIRS model assumes that recovered hosts are immune for a few time steps but then become susceptible again (hence the second S in SIRS) [26]. Initially, the population is seeded with only drug-susceptible pathogen strains and with a distribution of sequence types (STs) similar to what we find in the UK for E. coli [27]. After an initial period, treatment is started for randomly chosen infected hosts, which means that from there on, drug-susceptible strains have a probability t·e per time step to evolve to become drug-resistant due to mutation or acquisition of a genetic element. When a pathogen becomes resistant, it retains its ST identity. The cost of resistance is implemented as a reduction of the R0 value for drug-resistant strains relative to the R0 for the original susceptible strain, R0_res = R0_sus*(1-c) [28]. For simplicity, we ignore back-mutation, co-infection and treatment while a host is not yet infected. We implemented the model as a fully stochastic, individual-based model in the R programming language.
Results
In the resistance acquisition – negative selection balance model, there is strong positive selection for drug resistance within hosts on treatment and mild negative selection against drug resistance in the majority of hosts that are not on treatment. The mathematical model can explain the first two observations laid out in Figure 1. First, drug resistance stably co-exists with susceptibility at the level of t·e/c. Second, the level of resistance depends on the strength of positive selection and thus the usage of drugs at the population level, through the treatment parameter t. We then used individual-based simulations built on this model to confirm that the resistance acquisition – negative selection balance model can lead to many different resistant strains (i.e., resistance on different genetic backgrounds) in a population at any one point in time (see Figure 3A). The stable equilibrium that results from this model thus reflects the ongoing evolution of new resistant strains, of which some, due to chance, reach an appreciable level, but which ultimately all die out due to competition with the susceptible strain. This result leads to a clear prediction: Although the level of resistance is stable, “who” is resistant changes constantly. To determine whether this constant change is happening in reality we looked at temporal changes in the STs responsible for resistance in E. coli in the UK.
a: Simulations of the SIRS model with independently evolved drug resistant strains. Grey: isolates that don’t carry resistance, black: isolates that carry resistance. Pie charts: for select time points, the sequence type diversity of isolates that carry resistance. Each color represents one of the 100 most common sequence types or all other sequence types (orange). Parameter values: c = 0.05, e = 0.01, host population size = 20,000, R0sus = 2. Figure b: As a, for the main ciprofloxacin resistance mutation (S83L in gyrase A) in 37,000 E coli samples from the UK. Figure c: as b, but for isolates that carry the BlaTEM-1B gene. Data for 2B-C from Enterobase [27].
We analyzed a known resistance mutation (S83L in Gyrase A [29]), a known common resistance gene (BlaTEM-1B [30]) in 37,000 E. coli genome assemblies from the UK gathered over 15 years and downloaded from Enterobase [27]. First, we noticed that for both of these resistance mechanisms, the level of resistance is quite stable (Key Observation 1; Figure 3B-C). Next, we examined the data at a more granular level in hopes of seeing evidence for the waxing and waning of resistant strains that had independently evolved (whether by mutation or by acquiring a gene). E. coli strains are traditionally assigned to different multi-locus STs. Because STs are typically stable, resistance in different STs must be due to independent mutation or HGT. In Figures 3B and C, we show the level of resistance in the population and which STs are represented among the resistant isolates in pie charts. As predicted by our model, at any one time, resistance is due to mutations or genes carried by many STs (i.e., many colors in each of the pie charts in Figures 3B-C; Key Observation 3). We also note that in both our simulations and the empirical data, resistant strains appear and disappear dynamically. For example,BlaTEM-1B was initially carried mostly by the 131 sequence type, but later by 245 (3C).
Discussion
In order to understand, predict and influence levels of drug resistance in pathogens, we need mathematical models. Here we show that a simple stochastic model with strong positive selection for drug resistance within treated hosts and mild negative selection in the rest of the population can explain three key observations about drug resistance in a variety of pathogens (Figure 1A). First, the resistance acquisition – negative selection balance model we propose explains the stable coexistence of resistance and susceptibility in pathogen populations. Second, it explains the positive correlation between the amount of drugs used and the frequency of drug resistance (Figure 2). Finally, it recapitulates the simultaneous existence of many different strains that carry a resistance mutation or genetic element at any one time (Figure 3A). In addition to explaining these three key observations, our simulation results show that resistant strains increase and decrease in frequency, a behavior we observed in empirical data on ciprofloxacin resistance and two beta-lactamase genes in E. coli (Figure 3B-C).
A major strength of the resistance acquisition – negative selection balance model we propose is its simplicity. It relies on only a few assumptions and doesn’t require consideration of co-infection or spatial structure of the host population. One benefit of this simplicity is that the model is more likely to be applicable to many different pathogen systems. The most important assumption we make is that resistance always comes with a cost for the pathogen, reducing its R0 – if that is not the case, resistant strains will outcompete susceptible strains [31]. A major difference between our model and some previous deterministic models to explain stable coexistence of drug resistance and susceptibility [3,4] is that ours is stochastic and includes the creation and dying out of resistant strains, even when genetic elements that confer resistance are stable. One reason why researchers have chosen deterministic models over stochastic ones is because it is assumed that drug-resistant strains are stable. However, stability at the phenotypic level doesn’t necessarily mean stability at the genetic level. New strains may evolve resistance in the same way as previous strains, even acquiring genetic elements from previous strains. The result is that the genetic element or the mutation may be stably present, but “who” carries it may always be changing (Figure 3).
Another major strength of our model is that it makes clear and testable predictions. 1. It predicts that for a given drug, the higher levels of resistance in countries with high drug usage is due to the fact that resistance acquisition happens more often. We should therefore see more independently evolved resistant strains in countries with high levels of resistance. 2. The lifespan of resistant strains in a population should depend on the cost of the resistance for the pathogen. High-cost resistance should be associated with a shorter life span. 3. The time scale at which resistance levels change when treatment habits change should depend on the lifespans of resistant strains. Short life spans mean that a new equilibrium can be reached faster. These predictions can be used to determine for which pathogen systems the resistance acquisition – negative selection balance model works. Practically, the third prediction relating to how long it takes to reach a new equilibrium should be
Thanks to publicly available data, we were able to show that stability at the population level actually hides dynamic changes at lower levels (see Figure 3B-C). Although the resistance phenotype is present at a stable level (Figure 1A), and even the genetic elements that cause resistance are stable, the strains that carry the element are always changing (Figure 3-C). Although more detailed analysis is necessary, the E. coli data suggest that resistant strains may be around for several years before they disappear again. This observation is important because it indicates how long it would take for a new equilibrium to be established if treatment levels go up or go down. For example, if treatment with fluoroquinolones was halted entirely, we would expect that no new resistant strains would evolve and based on the data analyzed in this article it would take a couple of years for the existing strains to disappear. This information can be used for planning and evaluating interventions [32].
If stable levels of resistance do indeed mask the ongoing appearance of new resistant strains, this will have implications for machine learning methods that are used to predict drug resistance phenotypes from genomic data. At any given year and location, a machine learning algorithm may learn to recognize certain STs responsible for much of the resistance burden in a species. Yet, over time, resistance may wane in these STs and increase in others, which means that we likely need to re-train such models for current and local situations [33].
Our study has several limitations. One limitation is that we modeled resistance to a single drug and did not consider interactions between drugs or resistances. For example, when plasmids carry multiple resistance genes, resistance to one drug can be acquired due to selection for resistance to another drug. Our model also doesn’t explain why two seemingly unrelated resistances in some years occur on similar sequence types (Figure 3B and 3C). We also assumed that treatment does not affect transmission. If treatment itself is associated with strongly reduced transmission (as is the case in HIV), then this could in principle be modeled as a strong reduction of the R0 of resistant strains, but at least in the simulations it may be more realistic to include in the model the treatment state of hosts, where the transmission probability of hosts on treatment is significantly lower than those not on treatment [34,35]. The cost of resistance may also vary between strains and may be affected by compensatory mutations [31,36].
In conclusion, we propose a simple model that explains why drug resistance can stably co-exist with susceptible strains at levels that depend on drug usage. The model also explains why drug resistance is often present in many different strains (phylogenetic clusters, genetic backgrounds or sequence types) and predicts that resistant strains evolve and disappear again regularly. Data for ciprofloxacin resistance and beta-lactamase genes in E. coli are consistent with this prediction. This novel model has the potential to help us understand, predict and influence drug resistance levels and because of its simplicity, it can be readily tested in many different pathogen systems such as S. pneumoniae [2,3], S. aureus [4] and HIV [5,6]).
Data Availability
All data and code are on github: https://github.com/pleunipennings/CoexistencePaper
Methods
Code and data will be made available on github.
Figure 1A European surveillance data
Quinolone resistance over time in 10 European countries.
Data were downloaded from the European Surveillance Atlas for Infectious Diseases.
Link https://atlas.ecdc.europa.eu/public/index.aspx.
As health topic, we chose “Antimicrobial resistance”, as subpopulation “Escherichia coli|” and “fluoroquinolones” and as indicator “percentage resistance”. We then downloaded a csv file with data for all available years and regions. For Figure 1A we included the 10 most populous countries in the EU, including the United Kingdom: Germany, United Kingdom, France, Italy, Spain, Poland, Romania, Netherlands, Belgium, Czech Republic.
Figure 1B European surveillance data
For figure 1b, we used the percentage fluoroquinolone resistance in 2015 from the dataset described for Figure 1A, but now for the 20 most populous countries. This included in addition to the first 10: Sweden, Portugal, Greece, Hungary, Austria, Bulgaria, Denmark, Finland, Slovakia, Ireland.
For data on the use of fluoroquinolones in these countries, we downloaded data from https://www.ecdc.europa.eu/en/publications-data/antimicrobial-consumption-annual-epidemiological-report-2015 which included “Downloadable tables: Antimicrobial consumption - Annual Epidemiological Report for 2015”.
Figure 1CE. coli phylogenetic tree Kallonen dataset
The phylogenetic tree in Figure 1C was reproduced from [15]. Data presented here include only E coli strains from phylogroup D and F. The genomes and phenotypes were described in [37]. Briefly, a core genome alignment was used to create a phylogenetic tree, then we simulated a single history of the resistance phenotype using the “simmap” function in Phytools [38,39], the simulated history is shown on the tree with resistant branches in red, susceptible branches in green and intermediate branches in green.
Figure 3A individual based simulations
Simulations are run with a custom made R script. A population of hosts is initiated with 20,000 hosts (PopSize). Hosts can be
uninfected and susceptible to infection (“0”)
infected with a susceptible pathogen strain (“1”)
infected with a resistant pathogen strain (“2”)
recovered and not susceptible to infection (temporary immune) (“-1”)
20% of the hosts are initially labeled as infected with a susceptible pathogen strain (“1”) while the other 80% are labeled as susceptible (“0”). At the beginning of the simulation, the infected hosts are given a sequence type, randomly chosen from the 100 most common sequence types in the UK from the data described for Figures 3B and 3C. Each time step, three things happen:
All recovered (“-1”) hosts have a chance of 20% to become susceptible (“0”) again.
All infected (“1” and “2”) hosts have a chance to infect susceptible (“0”) hosts with their sequence type and resistance phenotype. For hosts that are infected with susceptible strains, the number of newly infected hosts is drawn from a poisson distribution with mean R0sus*(NumberSusceptible/PopSize), where R0sus is set to 2. For hosts that are infected with resistant strains, the R0 value is lower by the cost of resistance R0res = (1 - CostResistance)*R0sus. The cost of resistance is set to 0.05.
Starting from timestep 25, In each host that is newly infected with a susceptible pathogen strain, the pathogen can evolve to become resistant with probability RiskResistanceEvo, which is set to 0.01.
We keep track of the number of infected hosts, whether these infections are with susceptible and resistant pathogens and the sequence types of these infections.
Figure 3B
We started by going to https://enterobase.warwick.ac.uk/species/index/ecoli and downloading meta data for all E. coli from the UK. Importantly, we included the “Assembly Barcode (assembly stats)” and the “ST (Achtman 7-locus MLST)” for the multi-locus sequence type of the isolates through the experimental data tab. We then created a list of assembly barcodes (which end in _AS) and used it to download all genome assemblies to a local computer with a Python script.
Starting from the downloaded genome assemblies, we used Blast to identify the Gyrase A gene and determined the identity of the 83rd amino acid. We then calculated the fraction resistant as the number of isolates with L (7041 in total) divided by those carrying L or S (40445 in total) separated out for each year.
Figure 3C
Starting from the downloaded genome assemblies (as described for Figure 3B), we used the software Abricate (https://github.com/tseemann/abricate) to determine whether or not an isolate carried the BlaTEM-1B gene or not. We then calculated the fraction resistant as the number of isolates with the BlaTEM-1B gene (6741 in total) divided by those with or without the gene (38303 in total) separated out for each year.
Acknowledgements
I am grateful for comments from and discussions with Kristin Harper, Joachim Hermisson, Sarah Cobey, Alison Feder, Nandita Garud, Rasmus Nielsen, Alison Hill, Scott Roy and the students in the SFSU CodeLab.
Bibliography
